形式语言与自动机方法总结

知识结构，都是很基础的东西，可以查漏补缺

T1-3 DFA/NFA/正则表达式 设计

• 多练习设计
  一个小小的总结：
  

T4 正则语言泵引理

如果语言 L 是正则的, 那么存在正整数 N, 它 只依赖于 L, 对$\forall w\in L$, 只要|$w|\ge N$, 就可以将 $w$，分为三部分 $w=xyz$ 满足：

• 1. $y\ne \epsilon (|y|>0)$
• 2. $|xy|\le N$
• 3. $\forall k\ge 0,x{y}^{k}z\in L.$

T5&T6：

DFA转NFA

比较简单

NFA转DFA

子集构造法：

从开始状态{$q_0$}开始，构造子集，并对产生的集合继续构造，知道无法产生出新的集合，然后用转移函数画DFA即可

DFA转移正则语言

状态消除法

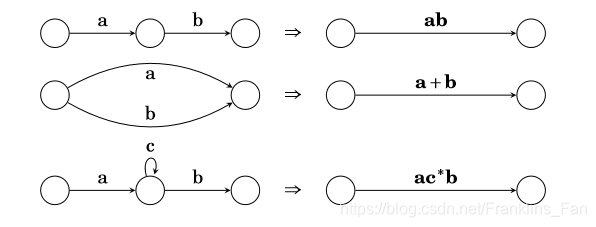
正则语言转换NFA

比较简单，将正则语言拆开，利用空转移增加开始和结束节点即可

DFA 最小化

使用填表算法
递归寻找 DFA 中全部的可区分状态对:

1. 如果 $p\in F$ 而 $q\notin F$, 则 [p,q] 是可区分的;
2. ∃a∈Σ , 如果 [r= $\delta$(p,a) , s=$\delta$(q,a)]

是可区分的 , 则 [p,q] 是可区分的

• 1.直接标记终态和非终态之间的状态对
• 2.标记所有经过字符 0 到达终态和非终态的状态对
• 3.标记所有经过字符 1 到达终态和非终态的状态对
• 4.此时对于未标记的状态对, 只需逐个检查，确定是否经过很短的字符串后, 都会到达相同状态，如果是，则是等价的，否则是可区分的

案例：

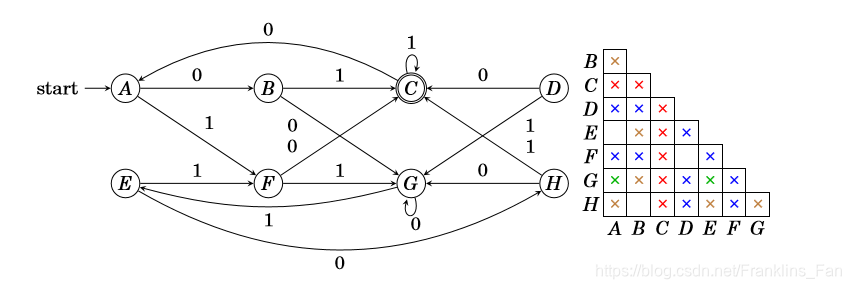
封闭性证明题

这种证明主要考察类似如果语言L是正则的，对L进行某种修改，问修改后的语言L‘是不是正则的
通常有两种证明方法:
1.使用运算的封闭性
有时候较为简单，比如证明：

min(L) = {w|w is in L, but no proper prefix of w is in L }.

的时候，对min()运算进行分析，可知 min(L)=L-L${\Sigma }^{+}$，然后就可以很容易的通过封闭性对其进行证明

但是有时候较为复杂，特别是涉及语言之间的同态问题，比如：

2.构造一个DFA，根据DFA和正则语言的等价性，来证明一个语言是不是正则的
通常是这样的流程

$已知的正则语言L->$DFA M:{$Q$,$\Sigma$,$\delta$,$q_0$,$F$}$->$DFA $M^{\prime }$:{$Q$,$\Sigma$,${\delta }^{\prime };$,$q_0$,$F^{\prime }$}$->$待证明的语言$L’$

1. 构造识别正则语言L的DFA 1，这个不需要具体构造，只需要写出其形式化定义即可
2. 构造识别新语言L‘的DFA 2,尝试变化一下转移函数，或者是接受状态，需要想一想
3. 证明新构造的DFA 2可以实别新语言L‘，需要证明充分性和必要性，就是∀w∈L(DFA),w∈L’ ∀w∈L(L’),w∈ DFA 即可

案例：

案例：

PS：集合运算英语词汇表

并集：union
交集：intersection
补集：complement
差集：difference
反转：reversal
闭包：closure
连接：concatenation
同态：homomorphism
逆同态：inverse homomorphism
代换：substitute

T7 文法设计，转换，化简

设计文法，就只设计，不需要化简

GNF概念需要掌握。转换方法中，消除直接左递归、消除间接左递归，了解即可。

CFG的设计

需要练习

CFG的化简

1. 消除 ε-产生式，首先 确定“可空变元”（能产生ε的变元），然后替换带有可空变元的产生式（替换后结果不能全为空）
2. 消除单元产生式，先确定“单元对” $A\to B\in P$, 则 [A,B] 是单元对; 然后消除单元产生式， 删除全部形为 $A\to B$ 的单元产生式;并将 B 的产生式添加到 A的产生式中。
3. 删除全部含有 ‘‘非产生的’’ 符号的产生式：如果 A→$\alpha$∈P 且 $\alpha$中符号都是产生的, 则 A 是产生的，否则A变不是产生的
4. 删除全部含有 ‘‘非可达的’’ 符号的产生式：如果从S出发不能到达A，那么A是非产生的

CNF文法转化

CFG转PDA

相对 PDA转CFG来说要简单，注意转换到的PDA都是空栈方式接受的

案例：

总结一下：产生空栈接受的PDA ，其中瞬时描述都为:

$(\epsilon ,每条产生式的左端变元/每条产生式的右端)$和 $(0,0/\epsilon )$和$(1,1/\epsilon )$

GNF转PDA

GNF的产生式都是 $S->a\alpha$的，其中a是终结符，α是由0个到n个的语法变元

总结一下规律，就是把之前的空转移换成GNF固定格式中的终结符，而右边的便是产生式的左端和产生的α（由0个到n个的语法变元组成）
总结一下，产生空栈接受的PDA，瞬时描述都为:

$(GNF产生式中的终结符,GNF产生式的左端变元/GNF产生式右端中的\alpha )$

PDA转CFG

这个比较复杂，但是仍有规律可循


看起来过程十分复杂，但是慢慢理解一下：利用PDA构造CFG，将CFG中每个文法变元视作为PDA的栈符号（因为都是中间产物），但是对于同一个栈符号，如果处于不同的状态，不能将其视作同一类，因此我们在前后加上之前之后的状态；例如对$qXp$，在PDA中表示的意义是从状态q弹出栈符号X到底状态p，然后我们便可以将栈符号转换为语法变元，从栈中一个个地弹出栈符号，会在输入带上一部分一部分消耗输入串，我们可以看成抵消的作用：即为了完全的弹出栈符号，需要消耗掉一部分输入串。
如果看不懂上面说的这些的话，不妨拿来主义地找点规律吧



可能画的比较乱，慢慢看就行

T8 PDA设计

同样需要练习
例题：
The set of all strings with twice as many 0’s and 1’s. (0 的个数是 1 的两倍)

一个很好的思路就是每读入1个1，就往栈中压入两个1，来保证0 的个数是 1 的两倍
但是在PDA中，转移函数中栈顶只能读一个符号，因此需要新建一个状态来处理
对于读入1的情况进行分类处理：

• 栈顶为1或空栈符号$Z_0$的时候，分两次向栈中压入1(共压入两个1)
• 栈顶为0的时候，弹出栈顶的0，如果弹出后的栈顶还为0的话，就利用空转移再弹出一个0，如果弹出后栈顶为1或为空栈，向利用空转移栈中压入一个1 来保证每个1可以消耗两个0

最后使用空栈的方式接受即可

T9 PDA 文法，转换，证明

泵引理：

封闭性：

特殊的一点：代换：
两个字母表 Σ 到 Γ 的函数 $s:\Sigma \to 2{\Gamma }^{\ast }$ 称为代换 ($substitution$). Σ 中的一个字符 a 在映射$s$ 的 作用下为 Γ 上的一个语言 $L_a$, 即
$s(a)=L_a$
扩展 s 的定义到字符串,

$s(\epsilon )=$ {ε}

$s(xa)$$=$$s(x)$$s(a)$

再扩展 s 到语言, 对$\forall L\subseteq {\Sigma }^{\ast }$,

之前提到的同态是把一个字符映射成另一个字符或字符串，而代换是把一个字符映射成一个语言

T10 图灵机设计

多练习构造

接受语言，停机时在接受状态即可；函数计算，停机时输入带结果正确即可。

语言识别器：

对于语言实别器，我们可以让不满足语法的输入卡住，最后在处理完后添加一个 B/B → 跳转到空状态
即可，例如：
实别：L = { $a_n$$b_n$$c_n$ | n ≥0 }
我们只需要 每轮依次判断X ，Y， Z然后跳转回X，如果过程中出现了少了某个字符，图灵机就会卡住，不能识别完跳转到接收状态，则说明输入不能被识别

然后我们給他添加一个死状态，保证能处理完所有的读入

同理，识别L = { $a_n$$b_n$$a_n$$b_n$ | n ≥0 }

识别： L = { w | w ∈ {0,1}* and |w| is 偶数}

案例：

函数构造器

函数构造器有时候会使用到 二进制计数器，这里提供一下设计其的策略“
观察二进制数逐个加一的规律：

• 0000
  0001
  0010
  0011
  0100
  …

可以发现，每个二进制数加一会产生两种情况：

• case1： 最后一位的0 $->$ 1，完成+1操作
• case2： 最后一位是1 $->$ 0, 往前推(1 $->$ 0),直到遇到最后一位是0然后0 $->$ 1，完成+1操作

因此我们可以设计一个图灵机，来实现+1计数器
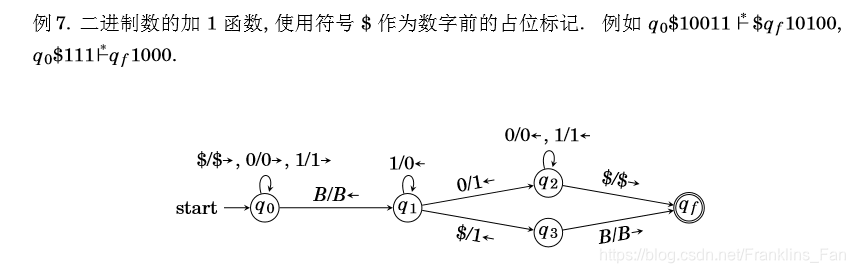
如下图所示：

案例：


这个案例可以将函数分为两个部分：读0部分 和 二进制计数器部分
首先为了方便实别，将串中全部的0改为字符Y，然后每从最右面的Y开始读取，将Y改为0，然后进行二进制+1，因为$0^n$的长度要始终大于其对于二进制数的长度，所有不会出现越界的情况，处理完全部的Y后，变开始清除无用的0，例如000100，我们需要去除前三个0，保留最后的100，才算完成处理工作。
案例：