关于齐次坐标以及绕坐标轴的旋转,需要提前了解,参考本博客的文章:【数学】齐次坐标、三维点/向量的平移、缩放、旋转
下面来推导绕任意轴(与轴的长度无关,则可以在计算前进行单位化为单位向量,也即
)旋转
角度的公式
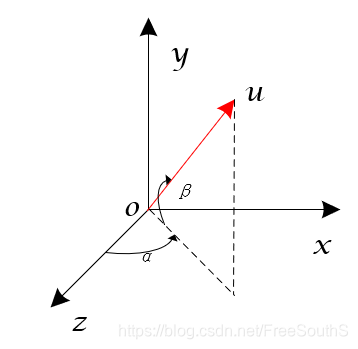
首先我们将看待为其由
轴,绕y轴旋转了
,又绕
轴旋转了
(逆时针是正,顺时针是负)。如果我们要求一个向量绕
旋转
的公式,我们可以先执行将
旋转到
轴的变换
,而后执行绕
轴旋转
,之后再执行
将
轴再移回
。由于有点绕,我们再分步骤详述一下:
- 将旋转轴
绕
轴旋转
转至
平面
- 将步骤1的成果绕
轴旋转
转至与
轴重合
- 绕
轴旋转
- 执行步骤2的逆过程
- 执行步骤1的逆过程

【步骤1】
现在我们来将执行第一个步骤,其旋转为绕
轴的普通旋转,其角度为
,旋转后形成向量
在
平面上,这个
就等于上图中将
投影到
平面上形成向量
,
与
轴的夹角:
我们首先来看绕轴旋转矩阵(参考:【数学】齐次坐标、三维点/向量的平移、缩放、旋转):
要将上述矩阵为已知值相关,则需要求出向量
的长度,其长度由
则长度为
,
其中,
则绕
轴的旋转矩阵记为
:
【步骤2】
我们首先来求向量的值,因为其是由
绕
轴旋转而来,因此其
不会变化为
,又因为旋转到了
平面上,因此其
值为0,而旋转不会导致长度发生变化为单位向量,则易求得其
分量为
,则
然后将步骤1的成果也就是向量,再绕
旋转个
(顺时针为负)即可。我们首先来看绕
轴旋转矩阵(参考:【数学】齐次坐标、三维点/向量的平移、缩放、旋转):
其中,
则绕旋转的矩阵记为
:
完成【步骤1】和【步骤2】以后,则向量与
轴完全重合执行步骤3
【步骤3】绕轴旋转
,则绕
轴旋转矩阵(参考:【数学】齐次坐标、三维点/向量的平移、缩放、旋转)记为
:
【步骤4】
因为旋转矩阵是正交矩阵,其逆矩阵与其转轶矩阵相等,因此【步骤4】只需要将【步骤2】转轶即可,得到:
【步骤5】
同理是【步骤1】的转轶,:
【最终】
我们得到绕任意单位向量旋转的结果为
:
,最终结果为:

























 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








