Transformer详细解读（通俗易懂，比较细节，基于论文《Attention Is All You Need》）

已于 2025-01-24 16:07:39 修改
阅读量1.1k 收藏 12
点赞数 32
文章标签： transformer 深度学习 人工智能
于 2025-01-24 13:43:43 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/FulcrumAC/article/details/145316624
版权

说明：1.本文章图片源于论文截图、个人绘制和其他标明出处的截图；2.比较基础的术语和操作在本文用【】强调，会做一些解释，如不理解请查阅其他资料~

1 编码器-解码器架构

        这里对应论文中的3.1 Encoder and Decoder Stacks，主要是对编码器和解码器的架构做简单说明，针对很多层的实现细节并不在本部分详细介绍。

1.1 这个架构的作用

        编码器的输入叫源，解码器的输入叫目标，训练的目的在于让源能够转换成目标。

        编码器将源（可能是一个句子）映射到潜空间（更低维度的空间），比如把一个句子中的每个词都映射到低维空间的一个向量上，这样做的好处是可以方便学习不同词之间的语义关联。

（这里多赘述一下，看不懂可跳过：我们可以思考如何把一个词映射为一个向量，最简单的考虑就是独热向量，也就是设计一个m维的向量，这个m表示了词语的数量，假设猫语这个语言体系一共有100个词，那么表示猫语中的每个词就需要100维的向量来表示，全部用0或1来填充。

但是这样表示并不好，因为所有向量都是正交的，很难计算相似度。计算相似度主要采取求内积的方式，但正交向量之间的内积不是0就是1，很难表示0.5,0.9这样的相似度。

所以，可以将词向量从独热向量映射成一个维度比较低的向量，这个新向量不只是用0和1来表示，因此可以计算更多相似度，再加上维度比较低，计算也快。这个新向量所在的空间就是潜空间。

编码器就是把源映射到潜空间，并学习词向量之间的语义关联。）

        解码器就是根据编码器学到的信息，生成目标序列。

        简单来讲，编码器学习如何抽取、表示原始数据的潜在关联，而解码器学习如何生成符合要求的目标数据。

1.2 编码器如何设计

        这段文字是论文中关于编码器部分的简单描述，这里基于以上内容做解读。可以结合下面的图片来理解。

        图片中，左边是编码器，由6个块组成，每个块就是图片中展示的那个样子。

        这个块中有两个层，第一个层叫【多头注意力机制】，即最下面那个橙色的层，第二个层是蓝色的Feed Forward层，每个层后面那个黄色的东西是layerNorm,即【层归一化】。而仔细观察图片会发现，橙色和蓝色方块的旁边还有一条“岔路”，这是【残差连接】操作。

下面解释一下LayerNorm是什么以及为什么选择它————————————————————

先通过与BatchNorm进行对比来理解LayerNorm的本质。

 

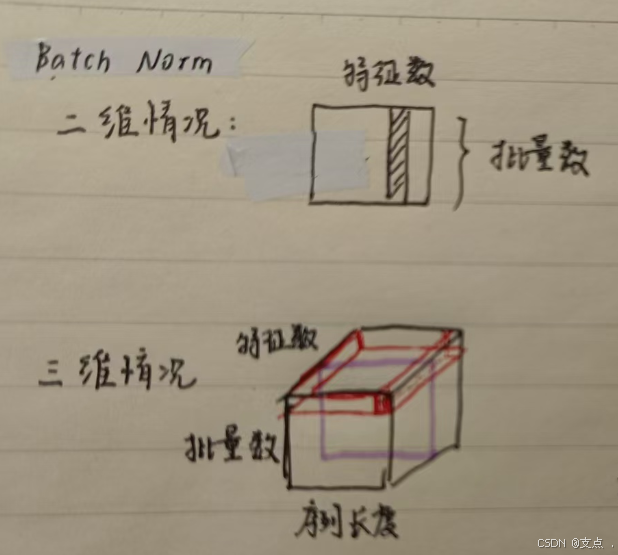
对于BatchNorm：

        在二维情况下，矩阵的一行表示一个样本，归一化操作的对象是一列（不同样本的同一个特征），所谓归一化可以简单理解为标准化（实际上还可以学习“缩放”和“平移”的参数，想进一步了解可查阅其他资料，这里可以先简单理解为标准化）。

        Transformer一般处理的是三维的张量，每一层（如红色所示）表示一个样本，归一化操作的对象是形如紫色所示的“片”。仍然是对不同样本的同一个特征做归一化。

对于LayerNorm：

        二维情况下，每行代表一个样本，归一化操作的对象是矩阵的一行，即一个样本内部进行标准化操作。

        三维情况下，仍是每层代表一个样本，归一化操作的对象是形如紫色的一层，即在一个样本内部进行标准化操作。

为什么Transformer选择了LayerNorm？

        咱们先回忆一下标准化操作是啥东西。比如x1，x2，x3，x4，x5去进行标准化操作，就是算出这五个数的均值μ和标准差σ，然后对每个xi，进行（xi-μ）/σ操作

        对比BatchNorm和LayerNorm，不难发现前者是针对不同样本的同一个特征进行标准化计算，这说明，计算μ和σ，受到所有样本的影响。我们知道，不同样本之间的序列长度是不一样的，经常需要对短序列填充一些0来统一长度，这会对归一化造成计算偏差。

        关于计算偏差这里详细解释一下。

        如图①，紫色是进行BatchNorm的对象，把它拿出来，如图②，不同样本的序列长度也不一样，黑色阴影部分表示不同长度的序列，红色细点区域表示应该填充0的区域，填充后，序列长度才统一。

        所以问题已经很明显了，本来实际有效的区域只是黑色区域，但现在多添加了很多0，一方面，多出来的0使得计算均值的总数变多，均值计算会偏小，另一方面，增加很多0可能会对数据的离散程度造成影响，使得标准差计算产生偏差。

        那么，LayerNorm为什么就不会有上述问题呢？

        这是因为，LayerNorm计算均值和标准差是每个样本内部进行计算的，哪怕样本大小不一样，计算均值和标准差也不会有什么偏差，因为各自玩各自的，哪怕不一样也没关系。

以上解释了LayerNorm是什么以及为什么选择LayerNorm———————————————

1.3 解码器如何设计

最低0.47元/天 解锁文章
支点 .
关注
Transformer详解
一去不复返的通信er
12-06 1189
transformer详解
【Transformer学习笔记】Transformer开山之作: Attention is All you Need
sjflsahfisaojfsa的博客
12-08 1959
这里写自定义目录标题一、transformer整体结构二、why Transformer三、Transformer逐层剖析1.Encoder 编码器词嵌入位置编码多头注意力机制层注意力机制多头encoder总结2.Decoder 解码器解码器输入mask机制双多头注意力机制输出 至今，transformer结构的网络可以说已经占据了RNN领域的大半壁江山，在各大RNN竞赛中基本都出现了霸榜的情况。 本文主要作transformer的开山之作《Attention is All you Need》的解读. 一、
09 大模型学习——Transformer详解
最新发布
weixin_54388827的博客
04-02 1643
从零开始，手撕transformer
经典重温：《Attention Is All You Need》详解
我爱计算机视觉
04-19 3964
关注公众号，发现CV技术之美本文位52CV粉丝投稿。原博客地址：https://blog.csdn.net/michaelshare/article/details/124178685该篇文章由谷歌大脑团队在17年提出，目的是解决对于NLP中使用RNN不能并行计算（详情参考《【译】理解LSTM（通俗易懂版）》），从而导致算法效率低的问题。该篇文章中的模型就是近几年大家到处...
Attention Is All You Need笔记
political_player的博客
09-12 578
是一类在自然语言处理和序列转换任务序列转换任务是指将一个符号序列转换为另一个符号序列的任务。例如在机器翻译中，把一种语言的文本序列转换为另一种语言的文本序列；在文本摘要生成中，将较长的文本序列转换为较短的摘要文本序列。）中使用的模型架构，其主要基于编码器 - 解码器的配置，利用复杂的递归神经网络（RNN）或卷积神经网络（CNN）。传统的显性序列转导模型基于 RNN 或 CNN 的架构存在一些局限性，比如RNN 存在顺序计算的约束，影响计算效率；CNN 在处理远距离位置的依赖关系时可能存在困难。而。
Attention Is All Your Need论文笔记
m0_62780794的博客
02-15 1556
作者提出了一个新的简单网络架构transformer。该模型是基于注意力机制，完全免去递推和卷积。模型的质量上更好，有着更好的并行性，训练地速度极大地减少，可以很好地泛化到其他任务中。
快速学会一个算法，Transformer
2401_82584055的博客
06-21 770
批量标准化是对一个批次中的所有样本进行标准化处理，它是对一个批次中的所有样本的每一个特征进行归一化。而层标准化是对每个样本的所有特征进行标准化处理，独立于同一批次中的其他样本。层标准化的优点是不受批量大小的影响，可以在小批量甚至单个样本上工作。更适合序列数据。
transformer详解
m0_72232218的博客
01-24 952
一个典型的编码器-解码器的结构，类似于sequence-to-sequence这6（可以自己定）个encode，decode在结构上是完全相同的，但是参数不是完全相同的训练的时候，不是训练了一个encode，然后copy 6次，而是6个encode多在训练。
Transformer全面详解
ssjdoudou的博客
07-12 7169
Time series on Transformer Transformer Input Transformer输入是一个序列数据，以"Tom chase Jerry" 翻译成中文"汤姆追逐杰瑞"为例： Encoder 的 inputs就是"Tom chase Jerry" 分词后的词向量。可以是任意形式的词向量，如word2vec，GloVe，one-hot编码。 假设上图中每一个词向量都是一个512维的词向量。 Postions Encoding(PE) transformer模型的attention
一文详解Transformer！！！
weixin_45683677的博客
03-13 1146
解决的问题 RNN 无法并行化，可以考虑使用CNN，但是CNN比较难考虑比较多的信息 这样的话self-attention 应运而生，self-attention可以看到双向的信息，并且b1–b4可以并行被训练出了。 模型原理 首选求出q,k,v b1得出： 只要控制αi，j是0或值那么就可以控制是否只看到local的值了 向量化 muti-head 不同的head可以看到不同的信息 local/far Pos-Encoding 在transformer中e_{i} 是直接加上的，W^{p}
transformer 属于TensorFlow吗
03-19
<think>嗯，用户问的是“Transformer属于TensorFlow吗？”首先，我需要确认用户的问题意图。可能用户对Transformer模型和TensorFlow框架的关系不太清楚，或者是在学习过程中遇到了混淆。 首先，我应该回忆一下Transformer的基本概念。Transformer是一种由Google在2017年提出的神经网络架构，主要用于自然语言处理任务，比如机器翻译。它的核心是自注意力机制，能够处理序列数据，并且在很多任务上取代了传统的RNN和LSTM。 接下来，TensorFlow是Google开发的开源机器学习框架，用户之前的问题中已经了解了TensorFlow的功能。现在的问题是，Transformer是否属于TensorFlow。这里需要明确，Transformer是一个模型架构，而TensorFlow是一个框架，用来实现和训练各种模型，包括Transformer。 用户可能混淆了模型架构和框架的关系。比如，像BERT、GPT这些模型都是基于Transformer架构构建的，但它们可以在不同的框架中实现，比如TensorFlow或PyTorch。因此，Transformer本身并不属于TensorFlow，而是可以在TensorFlow中实现。 然后，我需要检查是否有官方实现的例子。比如，TensorFlow的官方文档或库中是否有Transformer的实现。例如，TensorFlow提供了Tensor2Tensor库，其中包含了Transformer的代码。另外，Hugging Face的Transformers库也支持TensorFlow，用户可以在TensorFlow中使用预训练的Transformer模型。 可能用户还关心如何用TensorFlow构建Transformer模型，或者是否必须使用TensorFlow才能使用Transformer。这时候需要说明，Transformer是架构，可以在多种框架中实现，TensorFlow只是其中之一。 另外，用户可能有更深层次的需求，比如他们是否需要在TensorFlow中使用Transformer，或者寻找相关的教程。这时候可以建议用户查阅TensorFlow的官方文档，或者提供一些示例代码链接。 最后，确保回答准确无误，避免技术术语的混淆，用通俗易懂的中文解释两者的关系，并给出实际应用的例子，帮助用户更好地理解。</think>### Transformer 与 TensorFlow 的关系 **简单回答**： **Transformer 是一种神经网络架构**，而 **TensorFlow 是一个深度学习框架**。Transformer 本身不属于 TensorFlow，但可以通过 TensorFlow 实现、训练和部署。 --- ### 具体说明 #### 1. **Transformer 的起源** - Transformer 是 2017 年由 Google 团队在论文《[Attention Is All You Need](https://arxiv.org/abs/1706.03762)》中提出的模型架构，其核心是 **自注意力机制（Self-Attention）**，最初用于机器翻译任务。 - 它是一个**通用的架构设计**，不依赖于任何特定框架。 #### 2. **TensorFlow 对 Transformer 的支持** 虽然 Transformer 不“属于” TensorFlow，但 TensorFlow 提供了以下支持： - **官方实现**：TensorFlow 的 [Tensor2Tensor](https://github.com/tensorflow/tensor2tensor) 库中最早实现了 Transformer。 - **高阶 API**：通过 `tf.keras` 或 `TensorFlow Hub` 可直接调用预训练的 Transformer 模型（如 BERT）。 - **灵活构建**：用户可以用 TensorFlow 自定义 Transformer 的编码器、解码器、注意力层等组件。 例如，以下代码片段展示了用 TensorFlow 实现自注意力机制的简化版本： ```python import tensorflow as tf class SelfAttention(tf.keras.layers.Layer): def __init__(self, d_model): super(SelfAttention, self).__init__() self.d_model = d_model self.Wq = tf.keras.layers.Dense(d_model) self.Wk = tf.keras.layers.Dense(d_model) self.Wv = tf.keras.layers.Dense(d_model) def call(self, x): q = self.Wq(x) # 生成查询向量 k = self.Wk(x) # 生成键向量 v = self.Wv(x) # 生成值向量 # 计算注意力权重 attn_weights = tf.matmul(q, k, transpose_b=True) attn_weights = tf.nn.softmax(attn_weights / tf.math.sqrt(tf.cast(self.d_model, tf.float32))) # 加权求和 output = tf.matmul(attn_weights, v) return output ``` #### 3. **实际应用场景** 在 TensorFlow 生态中，Transformer 被广泛用于： - **自然语言处理（NLP）**：如 BERT（TensorFlow Hub 提供预训练模型）、GPT 等。 - **多模态任务**：如 Vision Transformer（ViT）用于图像分类。 - **时间序列预测**：通过注意力机制捕捉长期依赖。 --- ### 常见误解澄清 - **误区**：“Transformer = TensorFlow 的某个库”。 **正解**：Transformer 是模型设计，TensorFlow 是实现它的工具之一。 - **误区**：“必须用 TensorFlow 才能使用 Transformer”。 **正解**：Transformer 也可用 PyTorch、JAX 等其他框架实现（如 Hugging Face 的 Transformers 库）。 --- ### 总结 - **Transformer 是架构**，TensorFlow 是工具。 - **TensorFlow 提供了便捷的接口和预训练模型**，帮助用户快速应用 Transformer。 - 如果你需要在 TensorFlow 中使用 Transformer，可参考： - [TensorFlow 官方 Transformer 教程](https://www.tensorflow.org/tutorials/text/transformer) - [TensorFlow Hub 的 BERT 模型](https://tfhub.dev/google/collections/bert/1)
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值