旋转卡壳——洋葱三角剖分

出处：http://blog.csdn.net/acmaker/article/details/3314201

洋葱三角剖分

给定一个平面上的点集， 目标是构造一个点集的三角剖分。 

从Lennes 1911年二次时间复杂度的源算法到Chazelle 1991线性时间复杂度的算法， 前人已经做了许多关于提高三角剖分算法效率的研究。 

这里的焦点是关于一种特殊的三角剖分， 一种基于对点集进行“剥洋葱皮”操作。 
考虑平面上一个有 n 个点的集合 S 。 计算 S 的凸包， 并且设 S' 为在凸包内的点集。 然后计算 S' 的凸包并且反复执行这个操作直到没有点剩下。 最后剩下了一个像鸟巢一样层层覆盖的凸包序列， 称为洋葱皮集合 S。 感谢Chazelle的算法， 这个结构能够在 O(n log n) 时间操作内实现。 

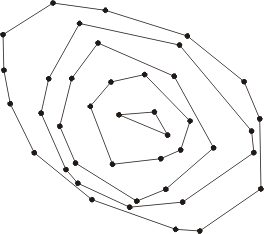一个点集的洋葱皮。 注意除了凸多边形外， 最里面的结构可能是一条线段或者是一个单一点。 这个图给出了点的层次信息， 比如点间哪个相对更“深”。

两个嵌套的凸包间的区域称为一个环面。 Toussaint在1986年发表了一个利用旋转卡壳计算环面三角剖分的简单算法。 利用这个方法， 一旦构造出洋葱皮， 就能在现行时间内构造出三角剖分。 进一步， 这个三角剖分有两个特点： 他的子图仍然是洋葱皮， 并且他是一个哈密尔顿图， 即三角剖分图的顶点可以是链状的。 

一个环面的三角剖分算法是非常简单的。 算法输入一个被凸包 P 包裹的凸包 Q， 他们的顶点都是顺时针序的。

1. 将凸包的边作为三角剖分的边插入。
2. 计算 P 和 Q 的 x 坐标最小的点， 分别称为 xmin(P) 和 xmin(Q) 。
3. 在 xmin(P) 和 xmin(Q) 处构造两条铅垂切线， 称之为 LP 和 LQ 。
4. 将 (xmin(P), xmin(Q)) 作为三角剖分的一条边插入。
5. 当前 LP 和 LQ 对应的 p 和 q 点分别是 xmin(P) 和 xmin(Q)。
6. 将线顺时针旋转直到其中一个与一条边重合。 一个新的顶点由此被一条线“击”出。
   • 如果他属于 P （称为 p'）， 插入 (p', q) 到三角剖分中。 更新当前的点为 p' 和 p' 。
   • 如果他属于 Q （称为 q'）， 插入 (p, q') 到三角剖分中。 更新当前的点为 p 和 q' 。
   • 对于平行边的情况， 两条切线都和边重合， 并且两个新的顶点被“击”出（称他们为 p' 和 q'）。 然后插入 (p', q') ， 以及 (p, q') 和 (p', q) 到三角剖分中。 更新当前的点为 p' 和 q' 。
7. 重复执行上述步骤直到达到开始的最小点。

一个换面的三角剖分如下所示：

 

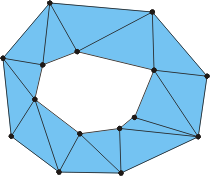
上述的算法拥有线性时间复杂度。 当对于一个点集进行三角剖分的时候， 一个凸包在整个过程中遍历（最多）两次， 最里面和最外部的凸包都只执行遍历一次。 因此对于一个 n 个点的三角剖分的总运行时间是 O(n)。 

另一个有效且与三角剖分有关的问题是基于点集的凸螺旋线的螺旋三角剖分。 

 

原文地址：http://cgm.cs.mcgill.ca/~orm/ontri.html