梯度下降

Gogool

于 2020-06-24 10:02:16 发布

阅读量389

点赞数

分类专栏： machine learning 文章标签： machine learning

本文链接：https://blog.csdn.net/Gogool/article/details/95005130

版权

machine learning 专栏收录该内容

2 篇文章 0 订阅

订阅专栏

2019.7.7

一、学习算法分类

监督学习

在监督学习中，对数据集中的每个样本，要算法预测得出正确答案，比如房子价格（回归）或者肿瘤是良性的还是恶性的（分类）。

回归（regression）问题：回归是指预测一个连续值输出

分类（classification）问题：分类是指预测一个离散值输出

problem：

problem1：货物数量和时间关系可以用函数表示，可看作连续。

problem2：是否被入侵可划分为0和1，0未入侵，1入侵，类似肿瘤为良性还是恶性两个离散值。

监督学习（supervised learning）

无监督学习

监督学习已经告诉什么是正确的什么是错误的，如肿瘤是良性还是恶性。无监督学习的每一个数据没有任何标签。

无监督学习(unsupervised learning)

聚类算法：得到一个数据，无监督学习可以将数据分为两个不同的簇，eg：谷歌新闻将网络上将新闻筛选并聚合在一起。

二、回归问题

单变量线性回归方程：

线性假设： $h(x)=\theta _{0}+\theta _{1}\cdot x$ ，（方差）平方差代价函数： $J(\theta _{0},\theta _{1})=\frac{1}{2m}\sum_{i=1}^{m}(h(x^{(i))})-y^{(i)})^{2}$ 。当 $min\frac{1}{2m}\sum_{i=1}^{m}(h(x^{(i))})-y^{(i)})^{2}$ 满足时，得到的θ0和θ1构成的线性假设方程为回归方程。x、y上标代表同一个变量取不同值。

首先在二维里讨论，只考虑θ1一个变量，设一个假设函数函数J(θ),取不同的θ值会发现函数成一个倒钟型，理论上会有一个拟合度最好的θ值，小于这个值或大于这个值都会使J(θ)变大。当J(θ)最小时，此时的θ构成的函数就是线性回归的目标函数

解决过程惯例公式如图

其次，考虑三维，设J(θ0,θ1)，不同θ值得到的J(θ0，θ1)函数最终构成如下平面，曲面高度代表J(θ0，θ1)值，类似于一个到碗状，碗底就是拟合最好的θ值。

我们把三维图转换为二维坐标上的等高线图，横坐标为θ0，纵坐标为θ1，在同一条直线上的说明拟合度一样，圈越小对应J(θ0，θ1)越小(该图无法显示J(θ0，θ1)值)，因为在圈上的点越少嘛，当最后只剩一个点时，得到目标函数。

所以我们的目标是利用算法使机器自己找到使J(θ0，θ1)最小的θ值，之后也会面=面临更复杂的例子、更多参数和更高维图形，将难以可视化，因此需要利用软件算法。

2019.7.8

梯度下降算法（gradient descent algorithm）

基础：

一阶泰勒公式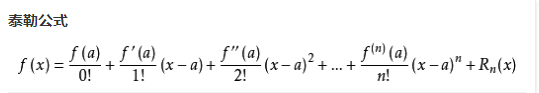

二阶泰勒公式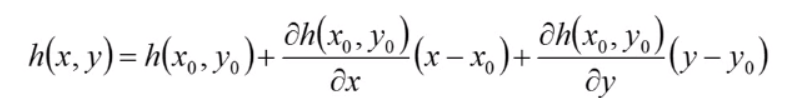

梯度：梯度的本意是一个向量(矢量),表示某一函数在该点处的方向导数沿着该方向取得最大值,即函数在该点处沿着该方向(此梯度的方向)变化最快,变化率最大。

梯度下降：寻找最优解的过程。梯度是函数上升最快的方向，因此下降最快的方向即梯度负方向。

大体思路：目的是寻找方差最小的函数拟合。通过代价函数偏导求得梯度下降最快的θ们值（依据泰勒公式），θ沿着最快方向一步步走到拟合函数方差最小的地方，即代价函数（方差）偏导为0。

赋初始θ值，θ值——>求代价函数——>求偏导——>求θ值

昨天说让机器自己找到使J(θ0，θ1)最小的θ值，就是今天探讨的梯度下降算法。

其特点是从不同的最高点位置出发，会下降到不同的局部最优解。

梯度下降算法公式如下图：

θ0、θ1要同步更新，过程如下：

算法中α取值不能过大，也不能过小，过小移动过慢，过大会可能收敛不了，下图为过大的情况，纵坐标为J(θ0，θ1)的值，开始∂J(θ0，θ1)/∂θ<0，J(θ0，θ1)呈下降趋势，计算 $\theta _{0}:=\theta _{0}-\alpha \cdot \frac{\partial J(\theta _{0},\theta _{1})}{\partial \theta }$ 由于α取值过大，导致θ0直接越过收敛点，再次计算此时∂J(θ0，θ1)/∂θ>0，θ0减小，由于|∂J(θ0，θ1)/∂θ|随着J(θ0，θ1)增大而增大，因此会越来越发散。

那么梯度算法如何进行计算？梯度下降和代价函数结合，得到线性回归算法，他可以用直线模型来拟合数据。我们把平方差代价函数 $J(\theta _{0},\theta _{1})=\frac{1}{2m}\sum_{i=1}^{m}(h(x^{(i))})-y^{(i)})^{2}$ 带入梯度下降算法中 $\theta :=\theta -\alpha \cdot \frac{\partial J(\theta _{0},\theta _{1})}{\partial \theta }$ 得到如下表达式，

7.10

矩阵方面知识大一已经建立了，快速的刷了一边，get到了一个小技巧

1、通过矩阵带函数变量，可推广到多元，这应该是用于机器上的计算处理比较方便

2、矩阵乘法：A*B！=B*A

3、A*B*C=A*(B*C)=(A*B)*C

逆矩阵是方阵

转置矩阵不一定是方阵

多元线性回归

多变量或多特征量，矩阵形式[ x0,x1 x2 .. xn] [θ0,θ1,θ2...θn]T

梯度下降算法变化为：

对每个偏导后，得到的梯度下降算法为:

$\theta _{j}:=\theta _{j}-\alpha \frac{1}{m}\sum_{i=1}^{m}(h_{\theta _{ }}(x^{(i))})-y^{(i)})x_{j}^{(i)}$

其中 $x_{j}^{(i)}$ 下标代表多元中一个变量，如x1，x2。上标代表每个变量取不同的值，它和对应的y构成图像里的点。

多元线性回归方程总的来说和单变量一模一样，只是在不同θ时，带入的 $x_{j}}$ 不同。

梯度下降运算中实用技巧Ⅰ——特征缩放

如果x1和x2范围差距过大会发生什么？也就是一个值变化对损失函数值影响很大，一个相对而言很小，如下由于x1小，因此θ1影响小。

我们还是利用老师的例子吧，：

x2 = size (0-2000 feet2)

x1= number of bedrooms (1-5)

这不θ是沿着梯度反方向变化，也就是切线的垂直方向，要是步长没把握好，就可能发生如下图情况，每次移动是挺长的，但下降的高度很小，呈之字形歪七扭八的。

幸运的话，步长控制好了，每次下降的可能会多些

要是选的出发点好，直线下去更好。

但不是效率最好的值不是一次两次就能试出来的，实际情况分析时不会图形化，有的高阶也难以图形化。

所以采用特征缩放的模式，将特征的取值约束到−1到+1的范围内.

如上题处理成：

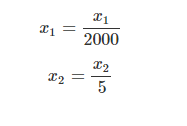
x1=x2，到达极值点会更直接，收敛所需迭代次数减少，学习率提高。具体缩放过程： $\frac{x-\mu }{s}$ ，u为训练集中特征x的平均值，s为该特征值范围。

梯度下降运算中实用技巧Ⅰ——学习率的（ $\alpha$ 的选择）

下图是一个横坐标为迭代次数，纵坐标为训练后J(θ)最值，越小拟合度越好。通过观察可知，训练次数越大，J(θ)越小，当到达200之后，J(θ)速度放缓。

$\alpha$ 的选值决定J(θ)的变化，过小会减小速度很慢，过大有可能不能收敛，呈递增函数，选择合适的 $\alpha$ ：老师的方法是每隔三倍选取一个值，通过观察下图的图像变化决定上限和下限，在此区间取最大可能 $\alpha$ 值。

正规方程

在之前学习梯度下降的时候，我一直纳闷一件事情，为什么不采用求偏导的方式直接求出取极值时的特征值，也就是通过偏导，

如： $J(\theta _{0},\theta _{1},\theta _{2}...\theta _{n})$ ，通过如下式子：

$\frac{\partial J(\theta _{0},\theta _{1},\theta _{2}...\theta _{n})}{\partial \theta_{0} }=0$

$\frac{\partial J(\theta _{0},\theta _{1},\theta _{2}...\theta _{n})}{\partial \theta_{1} }=0$

...

$\frac{\partial J(\theta _{0},\theta _{1},\theta _{2}...\theta _{n})}{\partial \theta_{n} }=0$

联立求出θ0、θ1...θn的值，从数学角度分析是非常方便的，但后来我又思考了一下，这对计算机而言是比较困难的，因为这是一个解多元方程，不是带值计算，解比较浪费时间。

除此之外，老师提供了一种正规方程的代替方法。公式如下：

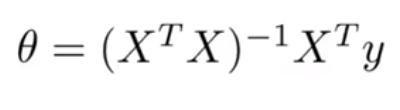
给个x的例子吧：

x是一个m*n的矩阵，m为样本数量，n为特征值数量+1，加了一个恒为1的x0是为了对应额外特征变量θ0。最后得到一个n*1的特征值向量。

梯度下降算法和正规方程法的对比

一般而言，正规方程法更适应于特征量少，在很多特征量的时候（>>10000)由于在进行运算时，有个O( $n^{3}$ )的过程，所以特征量越多，越耗时间。总之，在特征量少的时候，正规方程法是个代替梯度算法不错的选择。但在以后比较复杂的算法中，正规方程法仍不能实用这时会用原来的梯度下降。

梯度下降可以在很多特征量的时候很稳定的运行，其既适用于大量特征量的线性回归，也适用于之后的复杂算法中。

logistic算法

1、分类——（离散）：

① 二分类：y={0,1}

②多分类：y={0,1,2,3...}

分类不适合用线性回归的方法，因为它是离散的。阈值对应x点会随着样本值的变化而变化。假设有个二分类0和1，运用线性回归得到一条拟合直线，当y小于阈值为0，大于阈值为1，h(x)是个连续的有很多值，这样感觉没必要。

logistic算法是当下应用较广的分类算法，用于标签y为离散值0或1的情况。其会让 $0\leqslant h_{\theta }(x)\leqslant 1$ 。

logistic函数（sigmoid函数）： $h_{\theta }(x)=g(\theta ^{T}x)=\frac{1}{1+e^{-\theta ^{T}x}}$ ，其中 $g(z)=\frac{1}{1+e^{-z}}$ ，图像如下所示

可见当z->∞时，g(z)->1，z->-∞，g(z)->0，g(z)∈(0,1)，z=0过0.5的斜率先增大后减小的曲线。因此 $h_{\theta }(x)$ ∈(0,1)。有了这个假设函数h(x)，我们所要做的和之前一样，就是用θ拟合数据。

具体步骤：拿到一个训练集，给参数θ选定一个合适的值（之后会有一个算法拟合参数θ。

模型解释： $h_{\theta }(x)$ 的含义是对于一个输入x，y=1的概率估计。eg(肿瘤模型)：

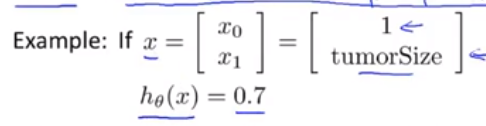
假如一个病人的肿瘤尺寸为x1，带入 $h_{\theta }(x)$ 后值为0.7，那么用数学表达式为P(y=1|x;θ)=0.7，含义是这个尺寸肿瘤为恶性的概率是0.7（估计要牵扯到贝叶斯了）

那么如何分类那？也就是何时将y预测为0，何时为1？

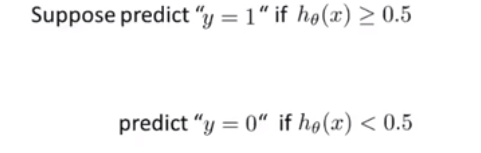
而由图像观察可以发现，当z<0时，h(z)<0.5,反之...，因此在假设函数中，当 $\theta ^{T}x$ >0，y=1， $\theta ^{T}x$ <0,y=0。

eg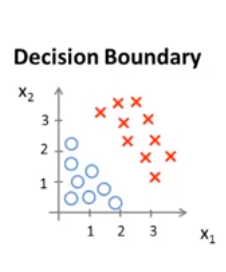：，求其假设函数，满足红色区域y=1，蓝色y=0。设，令θ0=-3，θ1=1，θ2=1。当y=1时，满足-3+x1+x2>0，y=0，满足-3+x1+x2<0。

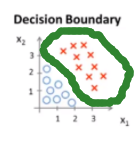
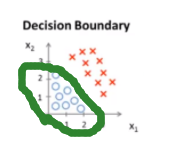
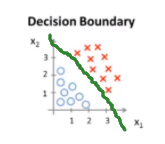
y=1区域 y=0区域决策边界

eg2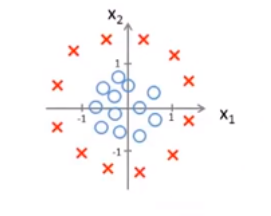：这个要在特征里添加高阶多项式项，设假设函数，令 $\theta ^{T}=[-1,0,0,1,1]$ ，得到当 $x{_{1}}^{2}+x{_{2}}^{2}>1$ ，y=1，反之y=0。

logistic代价函数(单训练样本)：

它的具体推导过程是最大似然估计法，https://blog.csdn.net/zengxiantao1994/article/details/72787849很不错

如果把线性回归里的代价函数J(θ)用于logistic回归中，会发现其图像可能如下：

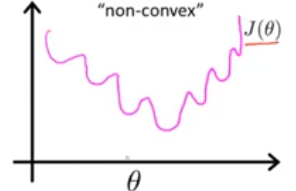
会有很多局部最优解，因为logistic里h(x)是个非线性嘛。所以代价函数不像线性回归一样是个凸函数，因此这种代价函数形式不适合logistic回归，我们选择下面一种代价函数。

上式等价成 $cost(h_{\theta }(x),y)=-ylog(h_{\theta}(x))-(1-y)log(1-h_{\theta}(x))$ 。

如果y=1，那么代价函数J(θ)如下图所示，当h(x)->1时，J(θ)->0，反之h(x)->0，J(θ)->∞（含义是我们告诉一个实际患恶性肿瘤的患者他患恶性肿瘤概率为0，这是不可能的，所以我们用最大最大的代价值惩罚算法），这是我们所希望的结果。

如果y=0，那么代价函数如下图所示，分析同上。

如何最小化代价函数J(θ)而训练出拟合集θ？

梯度下降法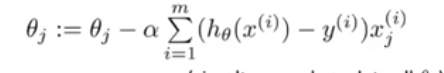，它的式子和前面完全一样，但是h(x)的含义不同，线性的 $\theta ^{T}x$ ，logistic的是 $\frac{1}{1+e^{-\theta ^{T}x}}$ 。

高级优化算法

前个讨论了利用梯度下降最小化logistic回归中的代价函数。高级优化算法相比于梯度下降算法大大提高优化效率。算法更适合解决大型机器学习问题。如：共轭梯度法、BFGS、L-BFGS..etc

高级优化算法的优点是：①不许要手动选择学习率 $\alpha$ ，它们自主尝试不同 $\alpha$ 值并自动选一个最好的 $\alpha$ ②收敛效率远远快于梯度下降。

具体的计算过程如下图，暂不解释。

多级分类

逻辑回归分类器：之前讨论的都是二分类问题，实际中有多分类问题，如天气：晴天雨天雪天。在处理时，可将多分类问题处理成多个二值分类。y={1...n}，将问题分割成n个二值分类问题，每个二值分类问题计算当前预测的y属于其中一个分类的概率。独立出来一组是正类别，其余是负类别。

Gogool

关注

0
点赞
踩
0

收藏

觉得还不错? 一键收藏
0
评论
梯度下降

2019.7.7一、学习算法分类监督学习在监督学习中，对数据集中的每个样本，要算法预测得出正确答案，比如房子价格（回归）或者肿瘤是良性的还是恶性的（分类）。回归（regression）问题：回归是指预测一个连续值输出分类（classification）问题：分类是指预测一个离散值输出problem：problem1：货物数量和时间关系可以用函数表示，可看作连续。...
复制链接

扫一扫