《Unsupervised Learning》+《PCA推导》
Unsupervised Learning
无监督学习可以分为:
- 化简为繁:将复杂的
i
n
p
u
t
input
input变成简单的
o
u
t
p
u
t
output
output;训练集数据只有
x
x
x,没有
y
y
y。
聚类( C l u s t e r i n g Clustering Clustering)
降维( D i m e n s i o n R e d u c t i o n Dimension\ Reduction Dimension Reduction) - 无中生有( G e n e r a t i o n Generation Generation):随机给模型一个数字,模型会生成不同的图像;训练集数据没有 x x x,只有 y y y。
Clustering
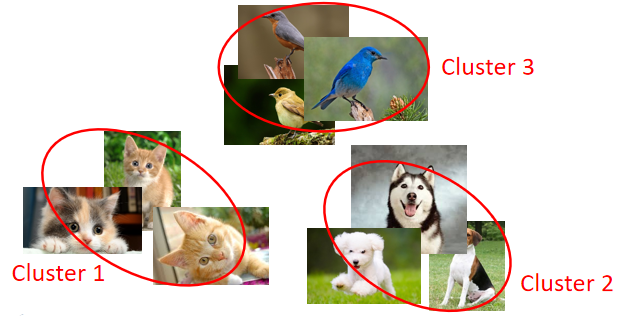
聚类:将数据样本按照相似度分成若干簇。如下图中没有 l a b e l label label的九张图片, C l u s t e r i n g Clustering Clustering任务就是将这九张图片按照相似度分成 3 3 3类:猫、狗、鸟。【这里的分类个数不是唯一的,也可成地上跑的、天上飞的两类】
K-means
聚类最常用的方法就是 K − m e a n s K-means K−means。任务是将数据集 X = x 1 , ⋯ , x n , ⋯ , x N X={x^1,\cdots,x^n,\cdots,x^N} X=x1,⋯,xn,⋯,xN分成 K K K个簇。
步骤如下:
-
S t e p 1 : Step1: Step1:选定簇的个数 K K K
-
S t e p 2 : Step2: Step2:从数据集中随机抽取 K K K个聚类中心 c i , i = 1 , 2 ⋯ , K c^i,i=1,2\cdots,K ci,i=1,2⋯,K
从 X X X中抽取的目的是保证每个簇都至少有一个样本点。 -
S t e p 3 : Step3: Step3:按照样本划分给最"近"的中心点
-
S t e p 4 : Step4: Step4:更新样本中心点(各簇的 f e a t u r e feature feature的平均值)
-
重复 S t e p 3 、 4 Step3、4 Step3、4,直到中心点收敛
Hierarchical Agglomerative Clustering (HAC)
聚类的其他方法: H A C HAC HAC
步骤如下:
-
S t e p 1 : Step1: Step1:建立一棵树;(类似哈夫曼算法)
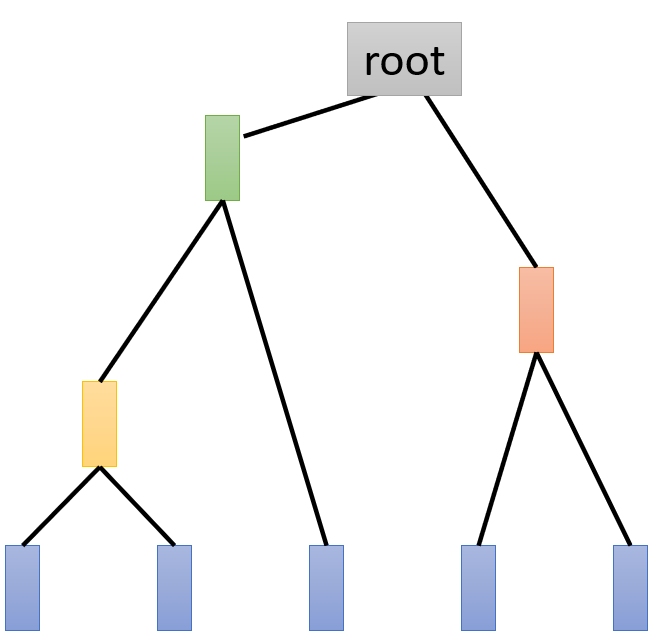
如下图,选择相似度最大的两个样本连接成一个新的结点,新节点的向量值为两个样本点 v e c t o r vector vector的平均;重复上述操作形成一颗二叉树。
-
选择一个 t h r e s h o l d threshold threshold进行裁剪;
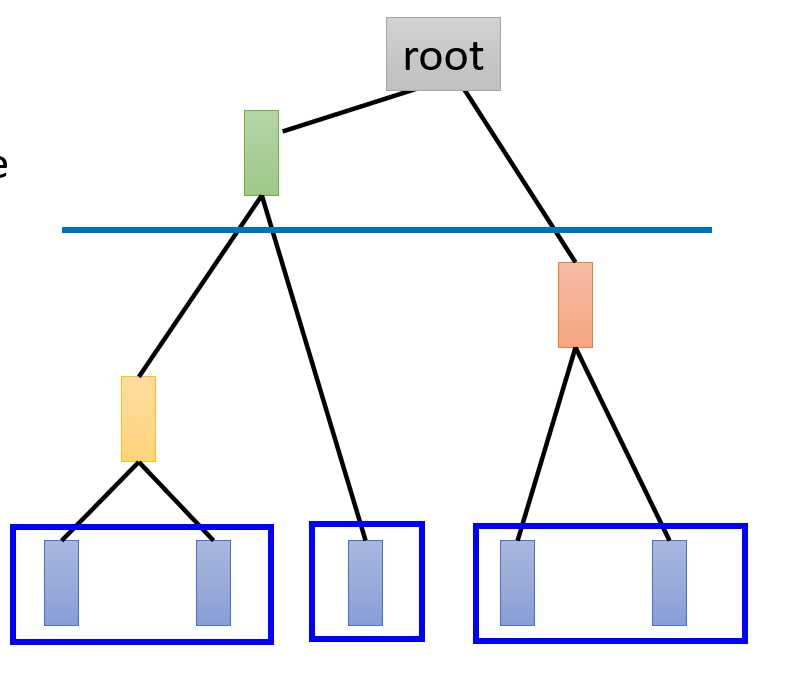
选取阈值然后“砍”树,如下图;在蓝色阈值处砍树后,可将数据分成三个簇。
再如下图,分成了三个簇:
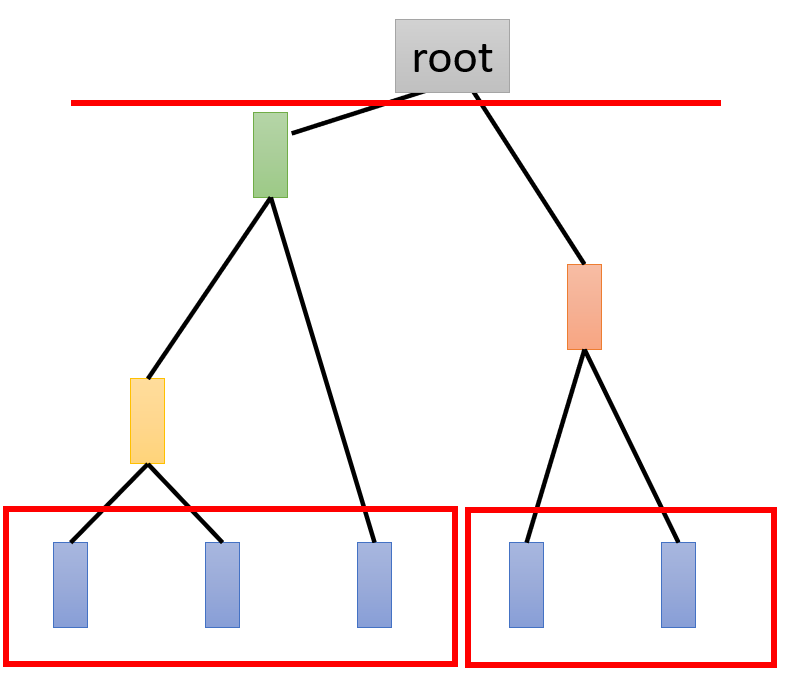
所以 H A C HAC HAC簇的数量取决于砍树的位置。
Distributed Representation
C l u s t e r i n g Clustering Clustering不太好的地方就是它会强迫样本点只属于某个类别,这样会丢失部分信息。正确的做法应该是使用一个 v e c t o r vector vector来描述样本点, v e c t o r vector vector的每个元素都代表这个样本点的属性。这种方法就叫做 D i s t r i b u t e d R e p r e s e n t a t i o n Distributed\ Representation Distributed Representation,或者叫做 D i m e n s i o n R e d u c t i o n Dimension\ Reduction Dimension Reduction。
如下图,某个角色都带有下面六个属性:
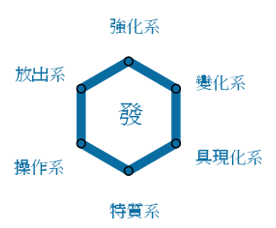
现在人物
A
A
A是处于强化系和放出系之间的,若使用
C
l
u
s
t
e
r
i
n
g
Clustering
Clustering来分类人物
A
A
A,结果会将
A
A
A分到强化系中去,从而失去了
A
A
A还带有放出系属性的信息;
D i s t r i b u t e d R e p r e s e n t a t i o n Distributed\ Representation Distributed Representation会对人物 A A A输出一个 v e c t o r vector vector,如下图,从 v e c t o r vector vector中不仅能知道 A A A有强化系,还有放出系的属性。
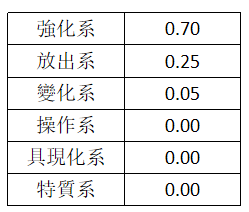
若人物 A A A原来的 f e a t u r e feature feature是高纬的,然后使用了一个低纬的 v e c t o r vector vector来描述 A A A;这个过程就叫做降维 D i m e n s i o n R e d u c t i o n Dimension\ Reduction Dimension Reduction
为什么降维能够有效呢?这里我的理解是某个维度上的冗余。
例如下图,存在不同的手写数字 3 3 3( 28 × 28 28\times28 28×28的图片),完全可以使用一维的旋转角度 θ θ θ来描述这一组 3 3 3,从而从 28 × 28 28\times28 28×28的 i m a g e image image变成了一维数据。(因为知道是数据 3 3 3了,所以表示数据 3 3 3的图片像素是冗余的,只需要知道旋转角度就能想象的图片的样子)
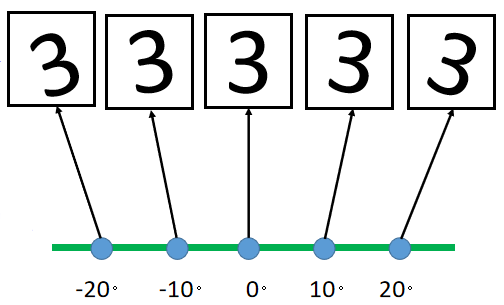
如何进行降维呢?
-
F e a t u r e s e l e c t i o n Feature\ selection Feature selection:从 f e a t u r e s features features中拿掉一些直观上对结果没有影响的维度。
如下图,从 x 1 、 x 2 x_1、x_2 x1、x2中拿掉 x 1 x_1 x1。
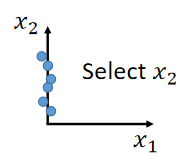
但是这个方法有时候并不管用,可能某两个维度之间都存在联系,拿掉谁都不合适。 -
P C A PCA PCA:吴恩达PCA笔记
P C A PCA PCA做的事情就是将原始数据 x x x投影到某个低纬度平面上,且确保最小程度的信息丢失。
假设要将 x x x映射成一维的,我们先要找一个一维平面 w 1 w^1 w1,然后价格 x x x投影到 w 1 w^1 w1上得到降维后的数据 z 1 z_1 z1。
z
1
=
w
1
⋅
x
z_1=w^1\cdot x
z1=w1⋅x

什么叫做最小程度的信息丢失呢?
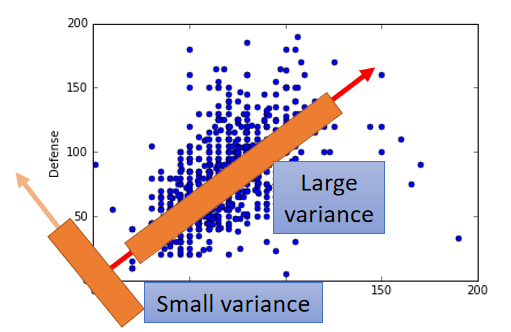
看下图,最小程度的信息丢失可以理解为降维后数据
z
1
z_1
z1要保留最大的方差
(
v
a
r
i
a
n
c
e
)
(variance)
(variance)。
【红色线条的维度上的信息就是降维后保留的数据信息,橙色的就是降维后去除的信息】
若要将 x x x降维成 n n n维的数据,那需要找一个 n n n维的平面 W W W,计算 x x x投影到 W W W上的值 z z z;且 z z z的方差最大
所以
P
C
A
PCA
PCA要做的事情就是找到
W
W
W,计算表达式:
z
=
W
⋅
x
z=W\cdot x
z=W⋅x
且
V
a
r
(
z
i
)
Var(z_i)
Var(zi)最大,
V
a
r
(
z
i
)
Var(z_i)
Var(zi)表达式:
V
a
r
(
z
i
)
=
1
N
∑
z
i
(
z
i
−
z
i
ˉ
)
2
Var(z_i)=\frac{1}{N}\sum_{z_i}(z_i-\bar{z_i} )^2
Var(zi)=N1zi∑(zi−ziˉ)2
即各维度都能最大化保留信息。
- z i z_i zi:降维后 z z z的第 i i i个元素,
- V a r ( z i ) Var(z_i) Var(zi)是对数据集中所有样本进行计算的
需要注意的一点是:
当我们求 w 1 w^1 w1时,需要计算 z 1 = w 1 ⋅ x z_1=w^1\cdot x z1=w1⋅x,即计算 x x x在 w 1 w^1 w1上的投影;且 w 1 w^1 w1满足 V a r ( z 1 ) Var(z_1) Var(z1)最大化。
当我们计算 w 2 w^2 w2时,也是上述同样的步骤;则算出来的 w 1 、 w 2 w^1、w^2 w1、w2都是一样的,为了确保 w 1 、 w 2 w^1、w^2 w1、w2不同,需要加上约束: w 1 、 w 2 w^1、w^2 w1、w2相互正交(即 W W W是一个正交矩阵)。
PCA推导
降维公式:
z
=
W
⋅
x
z=W\cdot x
z=W⋅x
任务:找到使 V a r ( z i ) Var(z_i) Var(zi)最大的 W W W。
先讨论 z 1 z_1 z1,降维公式
z 1 = w 1 ⋅ x z_1=w^1\cdot x z1=w1⋅x
任务:找到使 V a r ( z 1 ) Var(z_1) Var(z1)最大的 w 1 w^1 w1( W W W的第一行);
V a r ( z 1 ) = 1 N ∑ z 1 ( z 1 − z 1 ˉ ) 2 Var(z_1)=\frac{1}{N}\sum_{z_1}(z_1-\bar{z_1} )^2 Var(z1)=N1z1∑(z1−z1ˉ)2
假设 ∣ ∣ w 1 ∣ ∣ 2 = 1 ||w^1||_2=1 ∣∣w1∣∣2=1,即 w 1 w^1 w1是个单位向量。
为了更方便的寻找
w
1
w^1
w1;先将我们的目标
V
a
r
(
z
1
)
Var(z_1)
Var(z1)化简:
z
1
ˉ
=
1
N
∑
N
个样本
z
1
=
1
N
∑
w
1
⋅
x
=
w
1
⋅
1
N
∑
x
=
w
1
⋅
x
ˉ
\bar{z_1} =\frac{1}{N}\sum_{N个样本} z_1=\frac{1}{N}\sum w^1\cdot x=w^1\cdot \frac{1}{N}\sum x =w^1\cdot \bar{x}
z1ˉ=N1N个样本∑z1=N1∑w1⋅x=w1⋅N1∑x=w1⋅xˉ
V a r ( z 1 ) = 1 N ∑ z 1 ( z 1 − z 1 ˉ ) 2 = 1 N ∑ x ( w 1 ⋅ x − w 1 ⋅ x ˉ ) 2 = 1 N ∑ x ( w 1 ⋅ ( x − x ˉ ) ) 2 (1) Var(z_1)=\frac{1}{N}\sum _{z_1}(z_1-\bar{z_1})^2=\frac{1}{N}\sum_x(w^1\cdot x-w^1\cdot \bar{x})^2=\frac{1}{N}\sum_x(w^1\cdot (x- \bar{x}))^2\tag1 Var(z1)=N1z1∑(z1−z1ˉ)2=N1x∑(w1⋅x−w1⋅xˉ)2=N1x∑(w1⋅(x−xˉ))2(1)
而(下面式子随意转置的原因是
a
T
b
a^Tb
aTb是个标量):
(
a
⋅
b
)
2
=
(
a
T
b
)
2
=
a
T
b
a
T
b
=
a
T
b
(
a
T
b
)
T
=
a
T
b
b
T
a
(a\cdot b)^2=(a^Tb)^2=a^Tba^Tb=a^Tb(a^Tb)^T=a^Tbb^Ta
(a⋅b)2=(aTb)2=aTbaTb=aTb(aTb)T=aTbbTa
上式带入到
(
1
)
(1)
(1):
V
a
r
(
z
1
)
=
1
N
∑
(
w
1
)
T
(
x
−
x
ˉ
)
(
x
−
x
ˉ
)
T
w
1
=
1
N
(
w
1
)
T
∑
(
x
−
x
ˉ
)
(
x
−
x
ˉ
)
T
w
1
(2)
Var(z_1)=\frac{1}{N}∑(w^1)^T(x−\bar{x} )(x−\bar{x})^Tw^1=\frac{1}{N}(w^1)^T∑(x−\bar{x} )(x−\bar{x})^Tw^1 \tag2
Var(z1)=N1∑(w1)T(x−xˉ)(x−xˉ)Tw1=N1(w1)T∑(x−xˉ)(x−xˉ)Tw1(2)
令 1 N ∑ ( x − x ˉ ) ( x − x ˉ ) T = C o v ( x ) \frac{1}{N}∑(x−\bar{x} )(x−\bar{x})^T=Cov(x) N1∑(x−xˉ)(x−xˉ)T=Cov(x)为 S S S:
V a r ( z 1 ) = ( w 1 ) T S w 1 Var(z_1)=(w^1)^TSw^1 Var(z1)=(w1)TSw1
这个 S S S是关于对角线对称且是一个正定矩阵,所有特征值都是正数
所以任务变成了找到 w 1 w^1 w1,使 ( w 1 ) T S w 1 (w^1)^TSw^1 (w1)TSw1最大化,和一个约束条件: ‖ w 1 ‖ 2 = ( w 1 ) T w 1 = 1 ‖w^1‖_2=(w^1)^Tw^1=1 ‖w1‖2=(w1)Tw1=1。
可以想到使用拉格朗日乘数法(目标函数+
α
α
α约束条件):
g
(
w
1
)
=
(
w
1
)
T
S
w
1
−
α
(
(
w
1
)
T
w
1
−
1
)
(3)
g(w^1)= (w^1)^TSw^1−α((w^1)^Tw^1−1)\tag3
g(w1)=(w1)TSw1−α((w1)Tw1−1)(3)
对
w
1
w^1
w1的每个元素进行求导:
{
∂
g
(
w
1
)
∕
∂
w
1
1
=
0
∂
g
(
w
1
)
∕
∂
w
2
1
=
0
…
\begin{cases}∂g(w^1)∕∂w_1^1=0\\\\∂g(w^1)∕∂w_2^1=0\\…\end{cases}
⎩
⎨
⎧∂g(w1)∕∂w11=0∂g(w1)∕∂w21=0…
带入 ( 3 ) (3) (3),得到:
S w 1 − α w 1 = 0 Sw^1−αw^1=0 Sw1−αw1=0
即:
S
w
1
=
α
w
1
Sw^1=αw^1
Sw1=αw1
可以得出:要找的
w
1
w^1
w1其实就是
S
S
S的特征向量。
同时左乘 ( w 1 ) T (w^1)^T (w1)T:
( w 1 ) T S w 1 = V a r ( z 1 ) = α ( w 1 ) T w 1 = α (w^1)^TSw^1=Var(z_1)=α(w^1)^Tw^1=α (w1)TSw1=Var(z1)=α(w1)Tw1=α
可以得出:要找的 w 1 w^1 w1是 S S S的特征值 α α α最大的那个特征向量。
设 w 1 w^1 w1找到的特征值是 λ 1 λ_1 λ1;下面去找 w 2 w^2 w2;
任务:
找到
w
2
w^2
w2使
V
a
r
(
z
2
)
=
(
w
2
)
T
S
w
2
Var(z_2)=(w^2)^TSw^2
Var(z2)=(w2)TSw2最大,且
∣
∣
w
2
∣
∣
2
=
(
w
2
)
T
w
2
=
1
、
(
w
2
)
T
w
1
=
0
||w^2||_2=(w^2)^Tw^2=1、(w^2)^Tw^1=0
∣∣w2∣∣2=(w2)Tw2=1、(w2)Tw1=0
同样使用拉格朗日乘数法:
g
(
w
2
)
=
(
w
2
)
T
S
w
2
−
α
(
(
w
2
)
T
w
2
−
1
)
−
β
(
(
w
2
)
T
w
1
−
0
)
(4)
g(w^2)= (w^2)^TSw^2−α((w^2)^Tw^2−1) −β((w^2)^Tw^1−0)\tag4
g(w2)=(w2)TSw2−α((w2)Tw2−1)−β((w2)Tw1−0)(4)
对
w
2
w^2
w2各元素求导:
{
∂
g
(
w
2
)
∕
∂
w
1
2
=
0
∂
g
(
w
2
)
∕
∂
w
2
2
=
0
…
\begin{cases}∂g(w^2)∕∂w_1^2=0\\\\∂g(w^2)∕∂w_2^2=0\\…\end{cases}
⎩
⎨
⎧∂g(w2)∕∂w12=0∂g(w2)∕∂w22=0…
带入
(
4
)
(4)
(4)化简得:
S
w
2
−
α
w
2
−
β
w
1
=
0
Sw^2−αw^2−βw^1=0
Sw2−αw2−βw1=0
同时左乘
(
w
1
)
T
(w^1)^T
(w1)T:
(
w
1
)
T
S
w
2
−
α
(
w
1
)
T
w
2
−
β
(
w
1
)
T
w
1
=
0
(5)
\color{red}{(w^1)^TSw^2} \color{black}{−α}\color{blue}{(w^1)^Tw^2}\color{black}{−β}\color{green}{(w^1)^Tw^1}\color{black}{=0\tag5}
(w1)TSw2−α(w1)Tw2−β(w1)Tw1=0(5)
红色部分其实就是个标量,可以进行化简:
( w 1 ) T S w 2 = ( ( w 1 ) T S w 2 ) T = ( w 2 ) T S T w 1 = ( w 2 ) T S w 1 = λ 1 ( w 2 ) T w 1 = 0 (w^1)^TSw^2=((w^1)^TSw^2)^T=(w^2)^TS^Tw^1=(w^2)^TSw^1=λ_1(w^2)^Tw^1=0 (w1)TSw2=((w1)TSw2)T=(w2)TSTw1=(w2)TSw1=λ1(w2)Tw1=0
蓝色部分
w
1
、
w
2
w^1、w^2
w1、w2相互正交:
(
w
1
)
T
w
2
=
0
(w^1)^Tw^2=0
(w1)Tw2=0
绿色部分
∣
∣
w
1
∣
∣
||w^1||
∣∣w1∣∣等于1:
(
w
1
)
T
w
1
=
1
(w^1)^Tw^1=1
(w1)Tw1=1
带入(5),得到
β
=
0
β=0
β=0:
β
=
0
:
S
w
2
−
α
w
2
=
0
即
S
w
2
=
α
w
2
β=0:Sw^2−αw^2=0\ \ \ 即Sw^2=αw^2
β=0:Sw2−αw2=0 即Sw2=αw2
所以 w 2 w^2 w2也是 S S S的特征向量,避免与 w 1 w^1 w1重复,这里取 S S S第二大特征值对应的特征向量
总结 :
将 x x x降成 n n n维,求出 S = C o v ( x ) S=Cov(x) S=Cov(x)的特征向量,取前 n n n个最大特征值对应的特征向量组成 W W W,然后计算 z = W ⋅ x z=W\cdot x z=W⋅x, z z z就是降维后的 n n n维向量。
PCA-decorrelation
降维后的 z z z,计算其协方差 C o v ( z ) = D Cov(z)=D Cov(z)=D, D D D是一个对角矩阵。
推导过程如下:
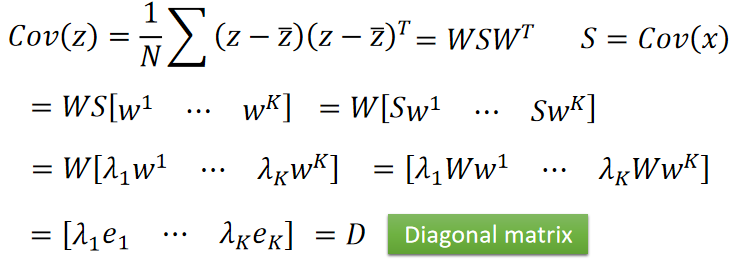
PCA降维后,不同维度之间的相关性变成0,即降维后的新 f e a t u r e s features features之间不存在联系。这样做的好处是:减少feature之间的联系从而减少模型所需的参数量
即降维后的 z z z不用考虑 z 1 ⋅ z 2 z_1\cdot z_2 z1⋅z2、 z 2 ⋅ z 3 z_2\cdot z_3 z2⋅z3等这些参数组合成的函数式,直接使用 z 1 、 z 2 、 z 3 、 … z_1、z_2、z_3、… z1、z2、z3、…即可。因此模型得到了简化,参数量也变少了,能够一定程度上避免过拟合。
Another Point of View
另一个视角看 P C A PCA PCA:
以手写数字为例子,我们可以将手写数字看作由若干
B
a
s
i
c
C
o
m
p
o
n
e
n
t
Basic\ Component
Basic Component组成;如下图,数字
7
7
7由
u
1
、
u
3
、
u
5
u^1、u^3、u^5
u1、u3、u5这三个
B
a
s
i
c
C
o
m
p
o
n
e
n
t
Basic\ Component
Basic Component组成。
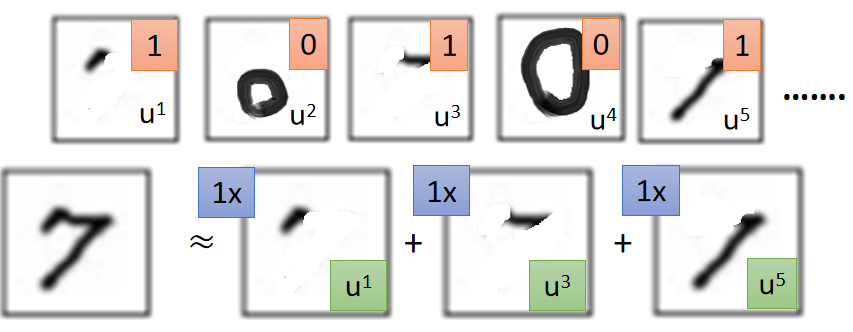
这样的好处是,使用 K K K个 v e c t o r vector vector就可以表示原来 28 × 28 28\times 28 28×28的手写数字图片了,即将 28 × 28 28\times 28 28×28的手写数字 x x x降维成 K K K个 v e c t o r vector vector的表现形式。
x
x
x的表达式如下:
x
≈
c
1
u
1
+
c
2
u
2
+
⋯
+
c
K
u
K
+
x
ˉ
x≈c_1u^1+c_2u^2+⋯+c_Ku^K+\bar{x}
x≈c1u1+c2u2+⋯+cKuK+xˉ
- x ˉ \bar{x} xˉ表示所有样本的平均
- c i c_i ci表示第 i i i个 B a s i c C o m p o n e n t Basic\ Component Basic Component的权重
将上述式子的
x
ˉ
\bar{x}
xˉ左移:
x
−
x
ˉ
≈
c
1
u
1
+
c
2
u
2
+
⋯
+
c
K
u
K
=
x
^
(1)
x−\bar{x}≈c_1u^1+c_2u^2+⋯+c_Ku^K=\hat{x} \tag1
x−xˉ≈c1u1+c2u2+⋯+cKuK=x^(1)
接下来我们的任务就是找到这 K K K个 B a s i c C o m p o n e n t Basic\ Component Basic Component,使 ∣ ∣ ( x − x ˉ ) − x ∣ ∣ 2 ||(x−\bar{x})−x||_2 ∣∣(x−xˉ)−x∣∣2最小;即找到最能表示 x − x ˉ x−\bar{x} x−xˉ的 K K K个 { u 1 , … , u K } \{u^1,…,u^K\} {u1,…,uK},最小化函数如下:

回顾之前的 P C A PCA PCA: z = W x z=Wx z=Wx;其实 W W W的 K K K个行向量就是使 L L L最小化的 { u 1 , … , u K } \{u^1,…,u^K\} {u1,…,uK}。
证明如下:
式子
(
1
)
(1)
(1)可写成下图的矩阵表示形式,最小化
L
L
L就是使下图两边的矩阵尽可能的相等。
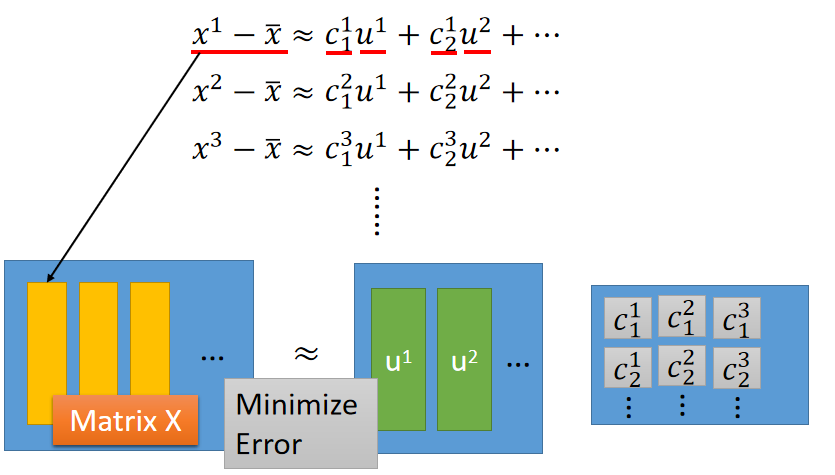
上图的矩阵 X X X可以通过奇异矩阵分解( S V D SVD SVD)来求解,如下图;矩阵 U U U就是 { u 1 , … , u K } \{u^1,…,u^K\} {u1,…,uK}, ∑ V \sum\ V ∑ V就是权重矩阵 c c c。

根据
S
V
D
SVD
SVD的结论,上图的
U
U
U的列向量是
X
X
T
XX^T
XXT的
K
K
K个最大特征值对应特征向量。所以
U
T
U^T
UT其实就是之前
P
C
A
PCA
PCA需要求的
W
W
W。
因此,PCA做的事情可以看作:找到最能近似表示原始数据 K K K个向量,最小化 L L L的过程。而PCA投影的结果就是权重矩阵 c c c
投影结果是c的证明:
X = U ∑ V = [ u 1 … u K ] c X=U \sum V=[u^1 … u^K]c X=U∑V=[u1…uK]c
.
U U U是正交矩阵,所以 U T = U − 1 U^T=U^{-1} UT=U−1,同时左乘一个 U T U^T UT,结果如下:
U T X = E ∑ V = E c = c U^TX=E \sum V=Ec=c UTX=E∑V=Ec=c
.
因为 U T = W U^T=W UT=W,所以:
W X = ∑ V = c WX=\sum V=c WX=∑V=c
PCA - Pokémon
举一个宝可梦的例子
假设一共有800只宝可梦,每个宝可梦由6个feature表示,所以我们使用PCA降维最多能降到6维;那么我们要降到几维呢?
可以通过降维后的6个特征向量对应的6个特征值来决定;假设第
i
i
i个特征向量对应的特征值为
λ
i
λ_i
λi,第i个特征值所占的比例
r
a
t
i
o
ratio
ratio为:
r
a
t
i
o
=
λ
i
λ
1
+
λ
2
+
λ
3
+
λ
4
+
λ
5
+
λ
6
ratio=\frac{λ_i}{λ_1+λ_2+λ_3+λ_4+λ_5+λ_6}
ratio=λ1+λ2+λ3+λ4+λ5+λ6λi
r
a
t
i
o
ratio
ratio计算结果如下:
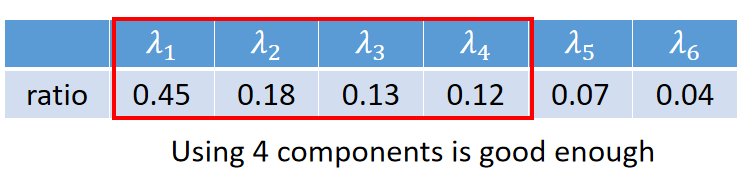
可以看出前4个特征值所占的比例较大,后两个影响较小,所以使用PCA降维到4维。
特征值 λ i λ_i λi的大小可以理解为将原始数据投影到对应特征向量 u i u_i ui后数据的离散程度(方差)。
λ i λ_i λi越大,离散程度越大,所能表示的信息就会越多
若这四个特征向量 P C 1 − 4 PC1- 4 PC1−4如下图所示(这里的 P C 1 − 4 PC1- 4 PC1−4相当于上面SVD的 u 1 − 4 u_{1-4} u1−4):
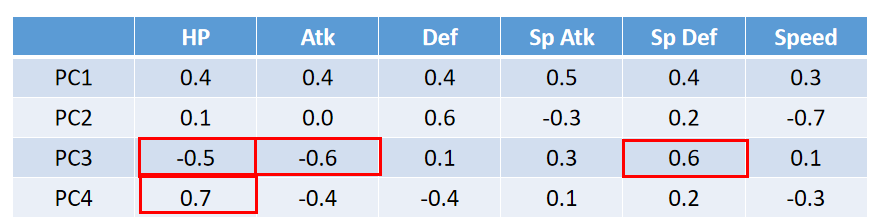
可以看出PC3可能表示的是具有特殊防御力,但攻击和血量较低的宝可梦;PC4可能表示的是血条比较高,但是速度比较慢的宝可梦。
将特征向量 P C PC PC与宝可梦的 f e a t u r e s v e c t o r features\ vector features vector做内积,可以得到宝可梦在该特征向量 P C PC PC投影的值,也代表了宝可梦的一个属性。如宝可梦与PC4做内积的值比较大,表示该宝可梦是一个血条比高的。
将800个宝可梦投影到PC3和PC4上(分别与PC3、PC4做内积),可视化如下:
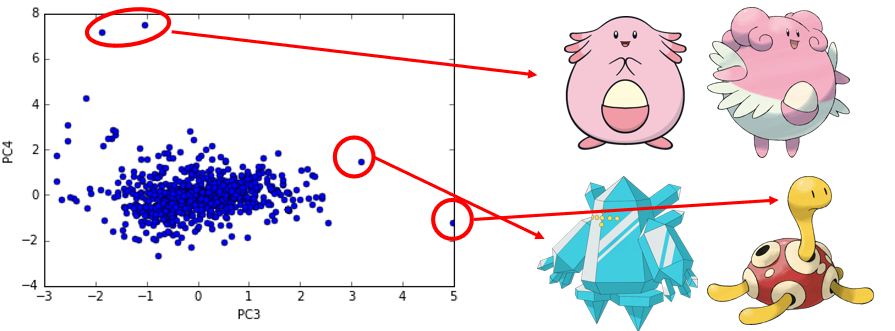
可以看出,左上角的两个点投影在PC4的值比较高,所以这两个宝可梦的血条会比较高;右下角的两个点投影在PC3值比较高,所以这两个宝可梦具有特殊的防御力。
PCA - MNIST
举一个手写数字识别的例子:
将手写数字识别降维到30维,则每个手写数字图像可表示为:
d
i
g
i
t
=
a
1
w
1
+
a
2
w
2
+
⋯
+
a
3
0
w
3
0
digit=a_1w^1+a_2w^2+⋯+a_30w^30
digit=a1w1+a2w2+⋯+a30w30
这里的
w
i
w_i
wi都是一张
28
×
28
28\times 28
28×28的图片;将
w
i
w_i
wi可视化后如下:
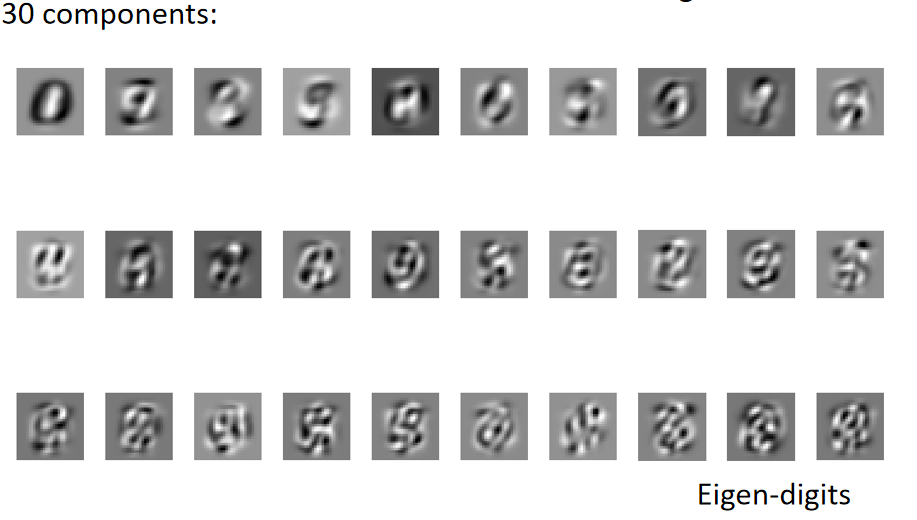
所有的手写数字图片都可以由这30个 B a s i c C o m p o n e n t Basic\ Component Basic Component线性表示。
可以看到很多 B a s i c C o m p o n e n t Basic\ Component Basic Component很抽象,想象不出怎么线性组成手写数字;这是因为在线性表示的时候,系数 a a a是可正可负的,即最后的手写数字的表示是由这些 B a s i c C o m p o n e n t Basic\ Component Basic Component加加减减组合成的,并不是向之前举例的数字7由简单的笔画相加而成。
NMF(non-negative matrix factorization)
若想要得到类似笔画的 B a s i c C o m p o n e n t Basic\ Component Basic Component,则需要使用非负矩阵分解,确保系数 a a a和 B a s i c C o m p o n e n t Basic\ Component Basic Component的数值都是正的。
对手写数据集采用 N M F NMF NMF后,对 B a s i c C o m p o n e n t Basic\ Component Basic Component的可视化结果如下所示:

可以看出使用
N
M
F
NMF
NMF后,手写数据图片可以由
B
a
s
i
c
C
o
m
p
o
n
e
n
t
Basic\ Component
Basic Component简单的线性相加组成;
B
a
s
i
c
C
o
m
p
o
n
e
n
t
Basic\ Component
Basic Component变成了数字的笔画。
Weakness of PCA
-
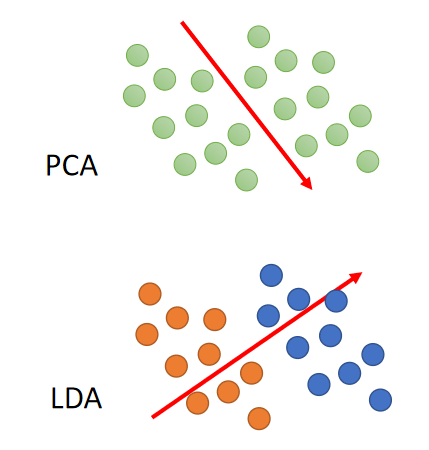
PCA是 U n s u p e r v i s e d Unsupervised Unsupervised的;如下图,PCA对数据进行降维后,可能橙色和蓝色的数据点就会混杂在一起,从而无法划分。(LDA是考虑了数据标签的降维方式,属于监督学习)
-
PCA是 L i n e a r Linear Linear的。如下图,我们希望能够将右上角的 S S S拉成一个平面,这是一个非线性的操作;但PCA做不到,PCA只整将 S S S压扁(投影)到某一个平面上。

Matrix Factorization(矩阵分解)
PCA中涉及到的一个思维是矩阵分解。
我们以宅男买手办为例子,如下图;
A
−
E
A-E
A−E分别表示5位宅男,表头表示4个不同的人物手办,表中的数据表示手办的购买数量。

如第一行第一个元素表示 A A A购买了5个第一个女角色的手办。
我们可以想象到,表中的元素值与宅男的特性和角色的特性是由关联的。假设宅男和手办角色背后都对应着呆(呆萌)和傲(傲娇)两个属性,如下图:
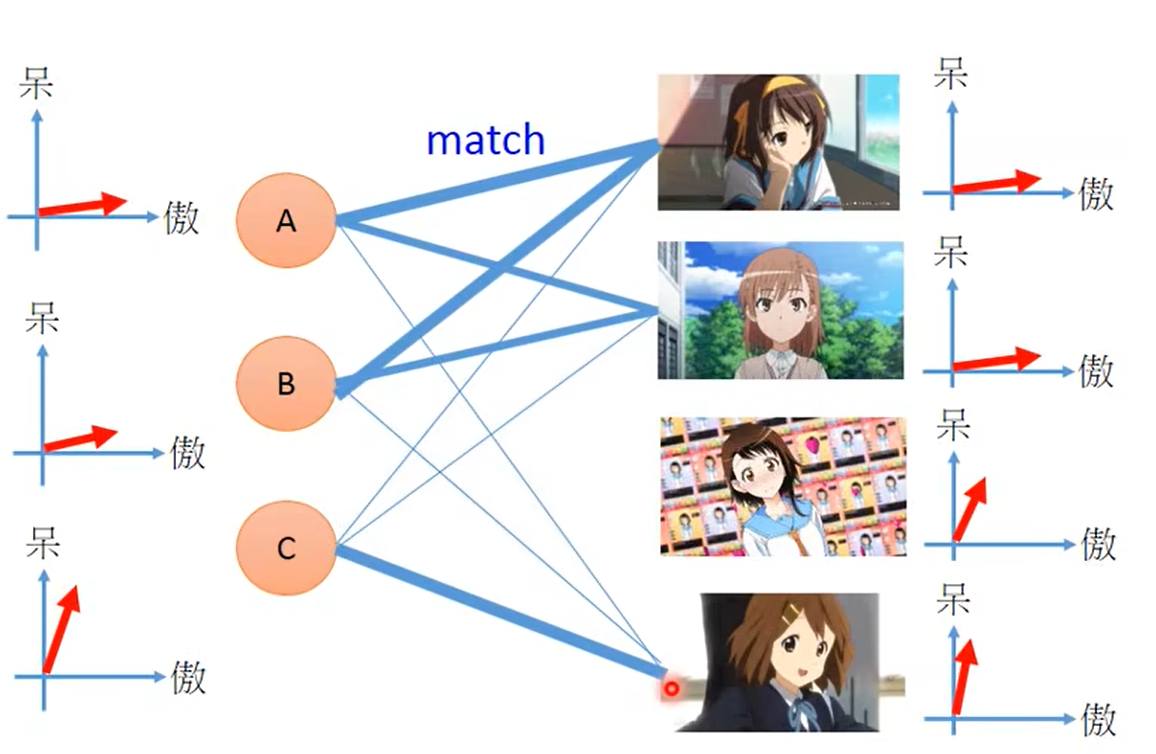
可以看到A与第一个角色都比较偏向傲娇,即A与第一个手办的内积(投影)值较大,所以A与第一个角色会更匹配,会购买较多的第一个女手办。
但在现实世界中,不一定会按照呆和傲这两个属性来决定表格中的数值。所以我们假设宅男背后的潜在特性为 r A … r E r^A…r^E rA…rE,人物背后的潜在特性为 r 1 … r 4 r^1…r^4 r1…r4;如下图:
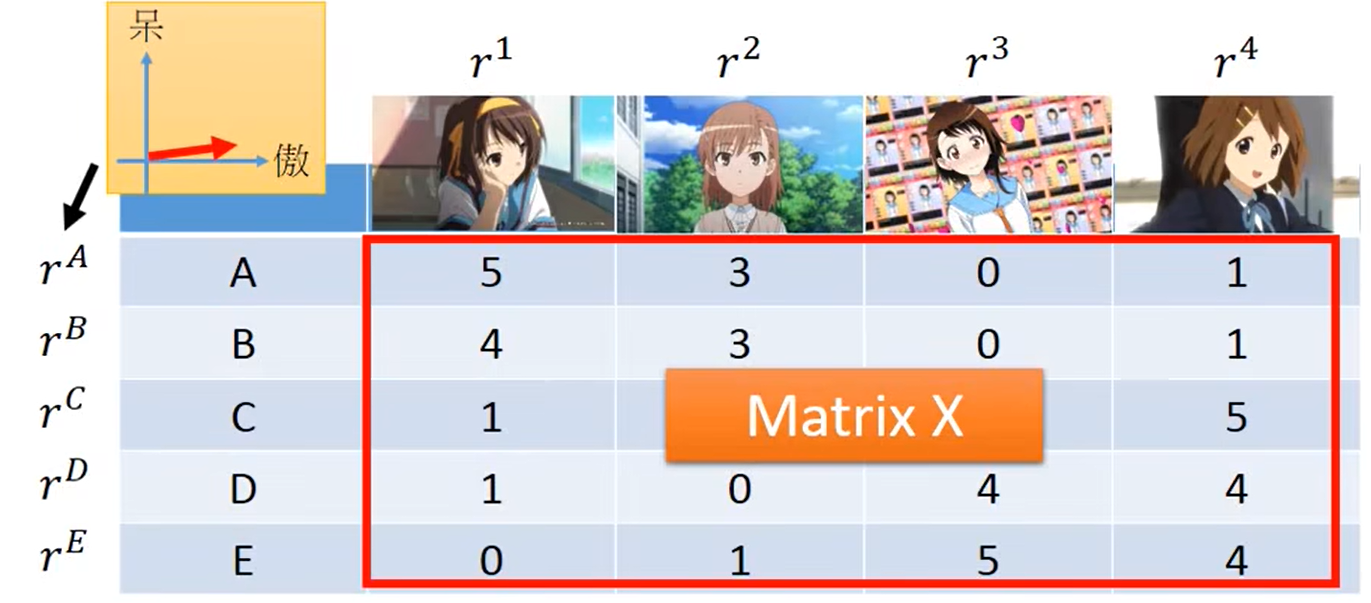
而表中的元素值由 r A − E r^{A-E} rA−E和 r 1 − 4 r^{1-4} r1−4内积计算,如下图:
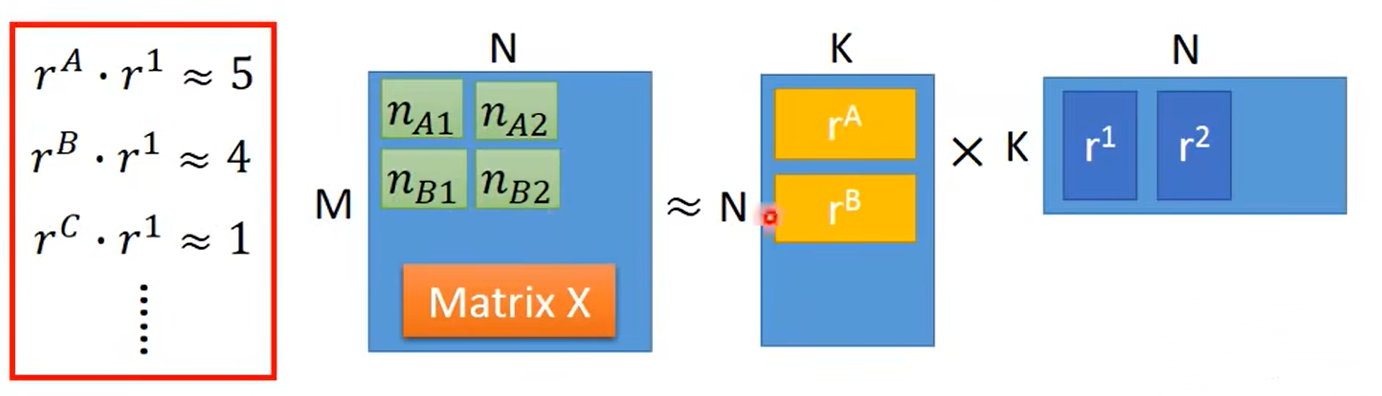
- M:宅男数量
- N:角色数量
- K:潜在特性的维度
对于上图的右侧的 r A − E r^{A-E} rA−E和 r 1 − 4 r^{1-4} r1−4可以通过SVD来计算,其中SVD分结后的 Σ Σ Σ可以归为 r A − E r^{A-E} rA−E,也可以归为 r 1 − 4 r^{1-4} r1−4。
如果存在表格元素缺失的时候,SVD就不能用了,我们可以使用梯度下降来计算
r
A
−
E
r^{A-E}
rA−E和
r
1
−
4
r^{1-4}
r1−4,如下图:

其中,仅对表中有数据的部分计算损失值,即表中的?不会对 L L L造成影响,通过梯度下降就可以计算出 r A − E r^{A-E} rA−E和 r 1 − 4 r^{1-4} r1−4了。
假设
r
A
−
E
r^{A-E}
rA−E和
r
1
−
4
r^{1-4}
r1−4计算结果如下:
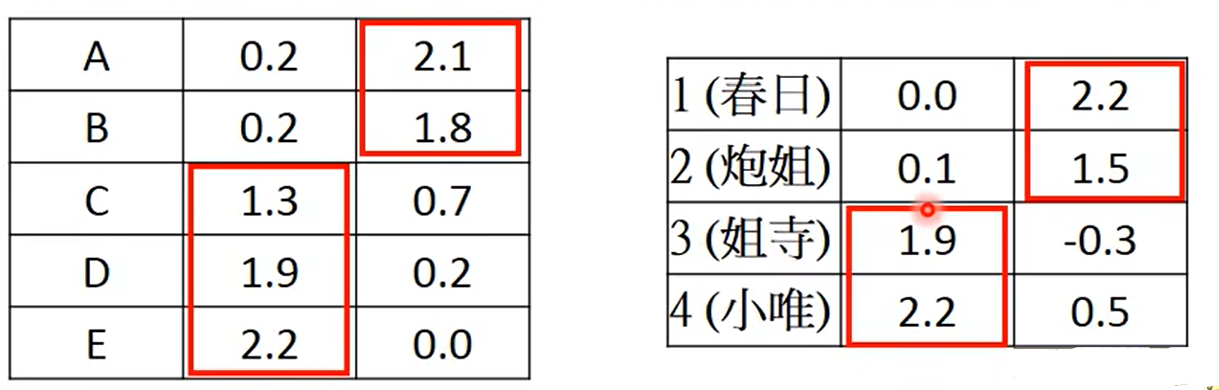
可以看出A和B宅男是比较类似的,角色1和2是比较类是的。
通过内积计算就可以预测表格中的缺失值了,如下图:
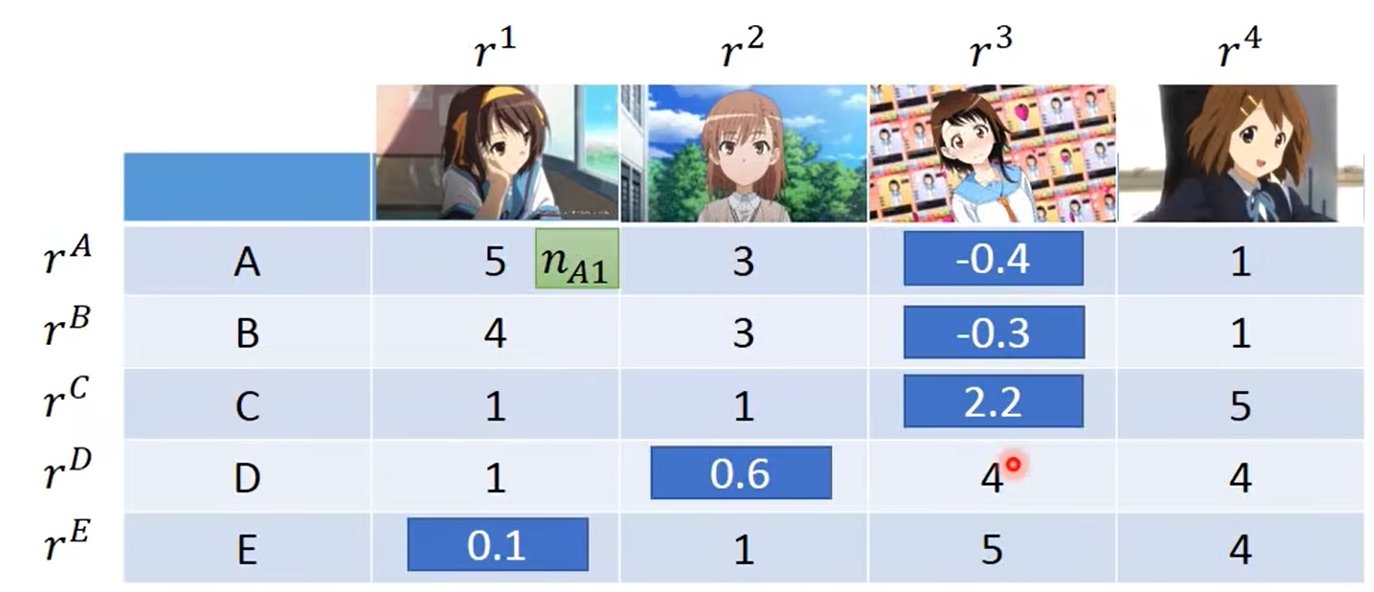
Matrix Factorization可以使用在推荐系统中,预测用户对某间物品的评分(这里相当于宅男购买手办的数量);具体可参考吴恩达老师的协同过滤推荐系统笔记。
为了考虑的更加全面,可以添加一些偏置参数;如
b
A
b_A
bA、
b
1
b_1
b1,
b
A
b_A
bA可表示A宅男有多喜欢买手办,
b
1
b_1
b1可表示角色1有多受欢迎。
则表中的元素计算式变为:

损失函数
L
L
L变为:

当然我们可以在
L
L
L中添加正则项;接下来就是梯度下降来寻找
r
A
−
E
r^{A-E}
rA−E和
r
1
−
4
r^{1-4}
r1−4。
Latent semantic analysis (LSA)
类似的例子可以出现在文章情感分析中,如下图,表格中元素代表某个单词的出现频率(Term frequency)。
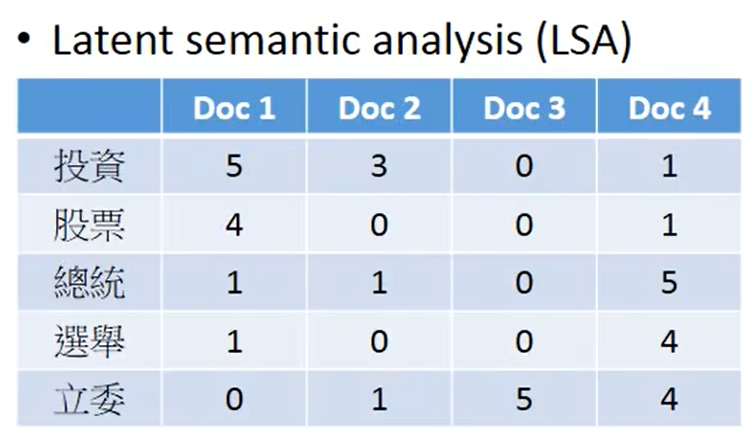
与之前不同的是,当我们使用表格中的元素Term frequency时,会乘上一个权重(inverse document frequency,逆文档频率);
因为我们希望常见词汇权重反而低,因为它普遍存在,使用的使用希望乘上一个较小的权重,减小对预测结果的影响。





















 1188
1188











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








