【无标题】

一
MATLAB里ode45命令用4阶龙格-库塔解一阶微分方程

% di/dt = L-1u - L-1(WL+R)i
function iprime = hw11_2(t,i)
L = [.0072, 0, 0, .1, .0054, 0;
0, .007, 0, 0, 0, .0026;
0, 0, .001, 0, 0, 0;
1.5*.1, 0, 0, 2.5, .125, 0;
1.5*.0054, 0, 0, .125, .0068, 0;
0, 1.5*.0026, 0, 0, 0, .0016];
W = zeros(6,6);
W(1,2) = -100pi;
W(2,1) = 100pi;
R = diag([.002,.002,.002,.4,.015,.015]);
u = zeros(6,1);
u(4) = 400;
iprime = L\u - L(W*L+R)*i;

主程序文件：调用ode45

% solve function hw11_2
theta0 = 0;
h = 1e-3; % step
i0 = zeros(1,6);
i0(4) = 400/.4;
ts = 0:h:1; % time span
[t,i] = ode45(‘hw11_2’,ts,i0); % solve
thetaA = 100pits + theta0;
thetaB = thetaA - pi/32;
thetaC = thetaA + pi/32;
n = length(ts);
ia = zeros(n,1);
ib = zeros(n,1);
ic = zeros(n,1);
% inverse Park transform
for j = 1:n
tt = ts(j);
thetaA = 100pitt + theta0;
thetaB = thetaA - 2pi/3;
thetaC = thetaA + 2pi/3;
ia(j) = cos(thetaA)*i(j,1) - sin(thetaA)*i(j,2) + i(j,3);
ib(j) = cos(thetaB)*i(j,1) - sin(thetaB)*i(j,2) + i(j,3);
ic(j) = cos(thetaC)*i(j,1) - sin(thetaC)*i(j,2) + i(j,3);
end
figure(1);
plot(ts,ia,‘y’,ts,ib,‘g’,ts,ic,‘r’);
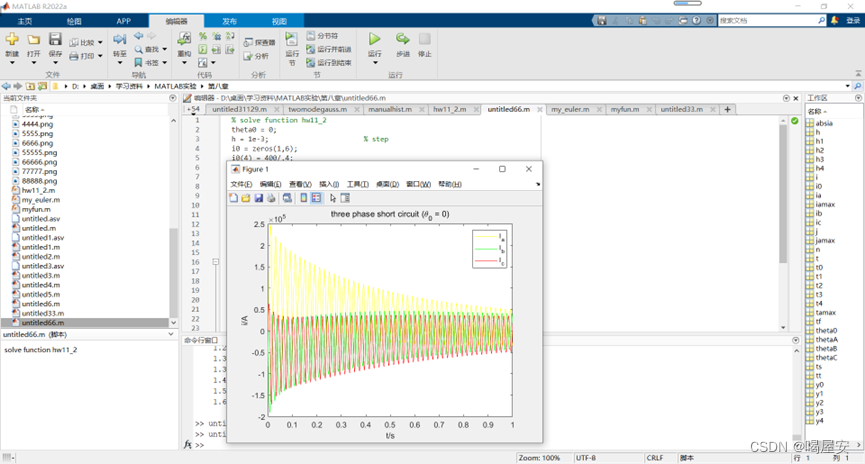
title([‘three phase short circuit (\theta_0 = ‘,num2str(theta0),’)’]);
xlabel(‘t/s’);ylabel(‘i/A’);
legend(‘I_a’,‘I_b’,‘I_c’);
absia = abs(ia);
[iamax,jamax] = max(absia);
tamax = ts(jamax);

二
%欧拉方法求解微分方程

function [t,y] = my_euler(f, t0, tf , y0, h)

%f-函数； t0，tf:区间； y0，初值；h 步长

M = floor((tf - t0)/h); % 离散点的个数

t = zeros(M +1, 1);

y = zeros(M +1, 1);

t = [t0 : h :tf]';

y(1) = y0;

for i =1:M

y(i+1) = y(i) + h*feval(f, t(i), y(i));

end

function s = myfun(t,y)

 s = 1/2*(t - y);

end
clear all;clc

%调用欧拉方法求解微分方程-

%函数原型 function [t,y] = my_euler(f, t0, tf , y0, h)

t0 = 0;tf = 3;

y0 = 1;

h1 = 1; h2 = 0.5; h3 = 0.25; h4 = 1/8;

[t1,y1] = my_euler(@myfun, t0, tf , y0, h1)

[t2,y2] = my_euler(@myfun, t0, tf , y0, h2)

[t3,y3] = my_euler(@myfun, t0, tf , y0, h3)

[t4,y4] = my_euler(@myfun, t0, tf , y0, h4)

plot(t1,y1,‘b>’,t2,y2,‘y*’ ,t3,y3,‘ro’,t4,y4,‘g–’);hold on;

xlabel(‘t’);ylabel(‘y’);grid on;

legend(‘h=1’, ‘h=1/2’,‘h=1/4’,‘h=1/8’);

plot(t4, 3*exp(-t4/2) - 2 +t4);

%第二种写法

% myfun1 = @(t,y)1/2*(t - y)

% [t,y1] = my_euler(myfun1, t0, tf , y0, h1)

% [t,y2] = my_euler(myfun1, t0, tf , y0, h2)

% [t,y3] = my_euler(myfun1, t0, tf , y0, h3)

% [t,y4] = my_euler(myfun1, t0, tf , y0, h4)

结果如下：

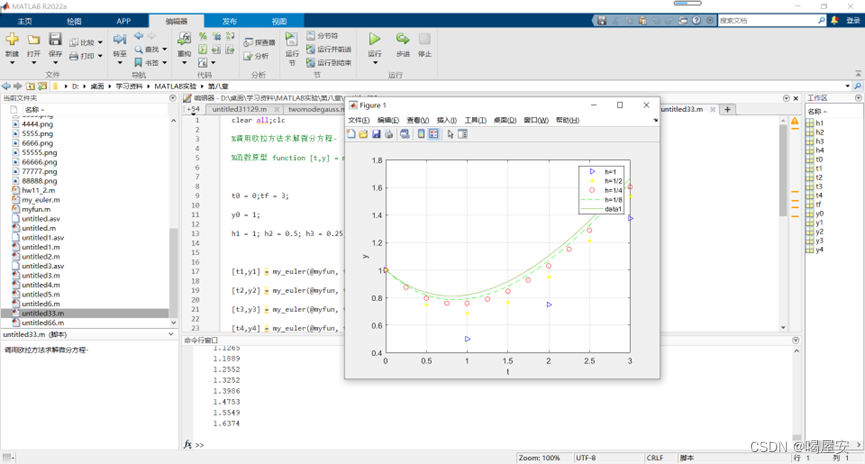
结论：可以看出，随着步长的减小，通过欧拉方法得到的微分方程的解，更加接近精确解。