WEEEEEEEEK14

最新推荐文章于 2024-11-10 10:39:34 发布
最新推荐文章于 2024-11-10 10:39:34 发布
阅读量66 收藏
点赞数
文章标签： 算法 c++ 数据结构 Powered by 金山文档
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/HEYONANA/article/details/129767366
版权

T1

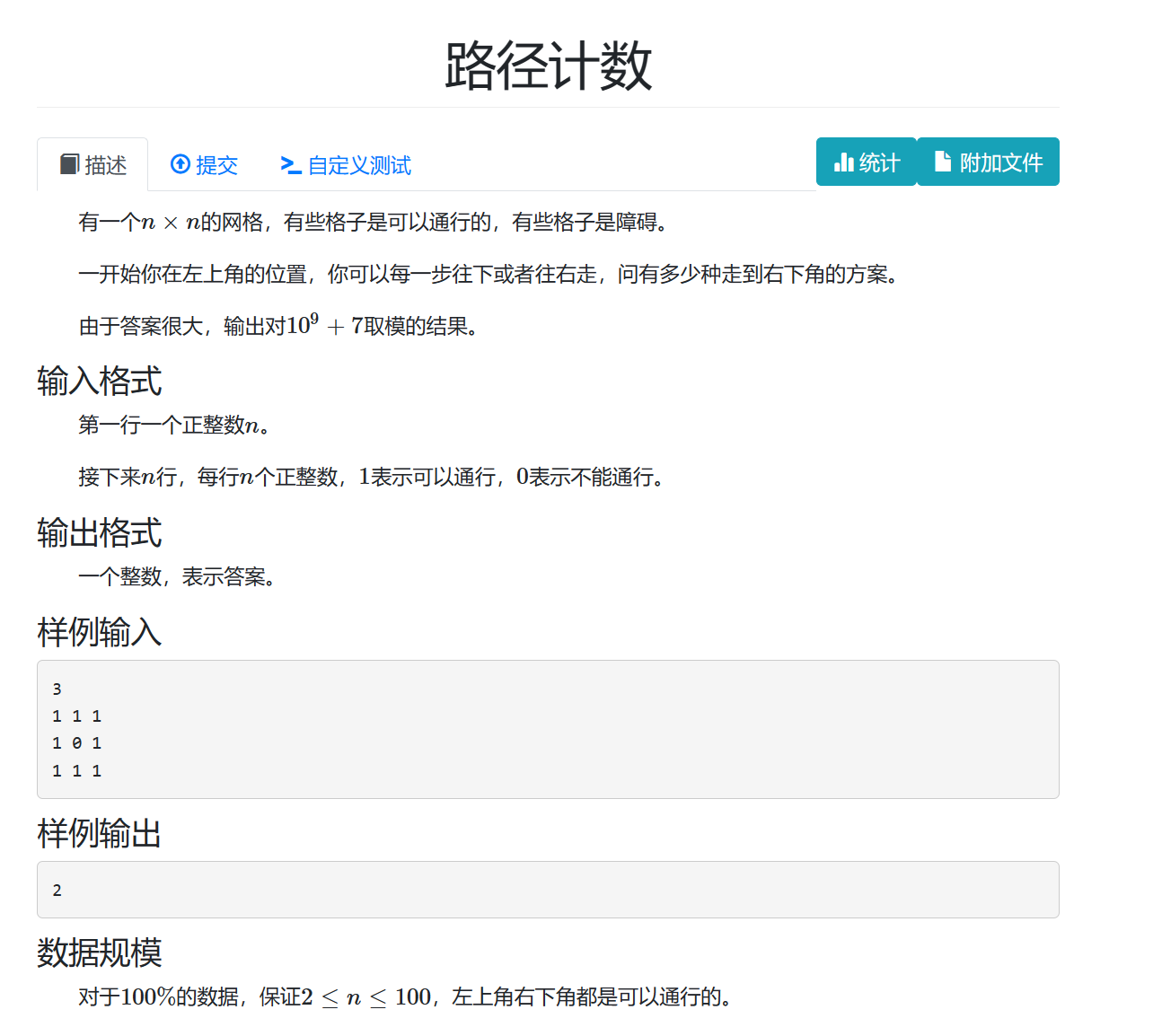
思路：开两个二维数组，一个用来记录能否通行，另外一个用来dp。

#include<iostream>
#include<string.h>
#include<set>
#include<utility>
#include<queue>
using namespace std;

int n;
 int m[105][105];
 long long f[105][105] = { 0 };

int main()
{
    scanf("%d", &n);
    for (int o = 1; o <= n; o++)
    {
        for (int i = 1; i <= n; i++)
        {
            scanf("%d", &m[o][i]);
        }
    }
    f[1][1] = 1;
    for (int o = 1; o <= n; o++)
    {
        for (int i = 1; i <= n; i++)
        {
            if (m[o][i] == 1)
            {
                f[o][i] += f[o - 1][i] + f[o][i - 1];
                f[o][i] %= 1000000007;
            }
        }
    }
    printf("%lld", f[n][n]);
    return 0;
}

T2

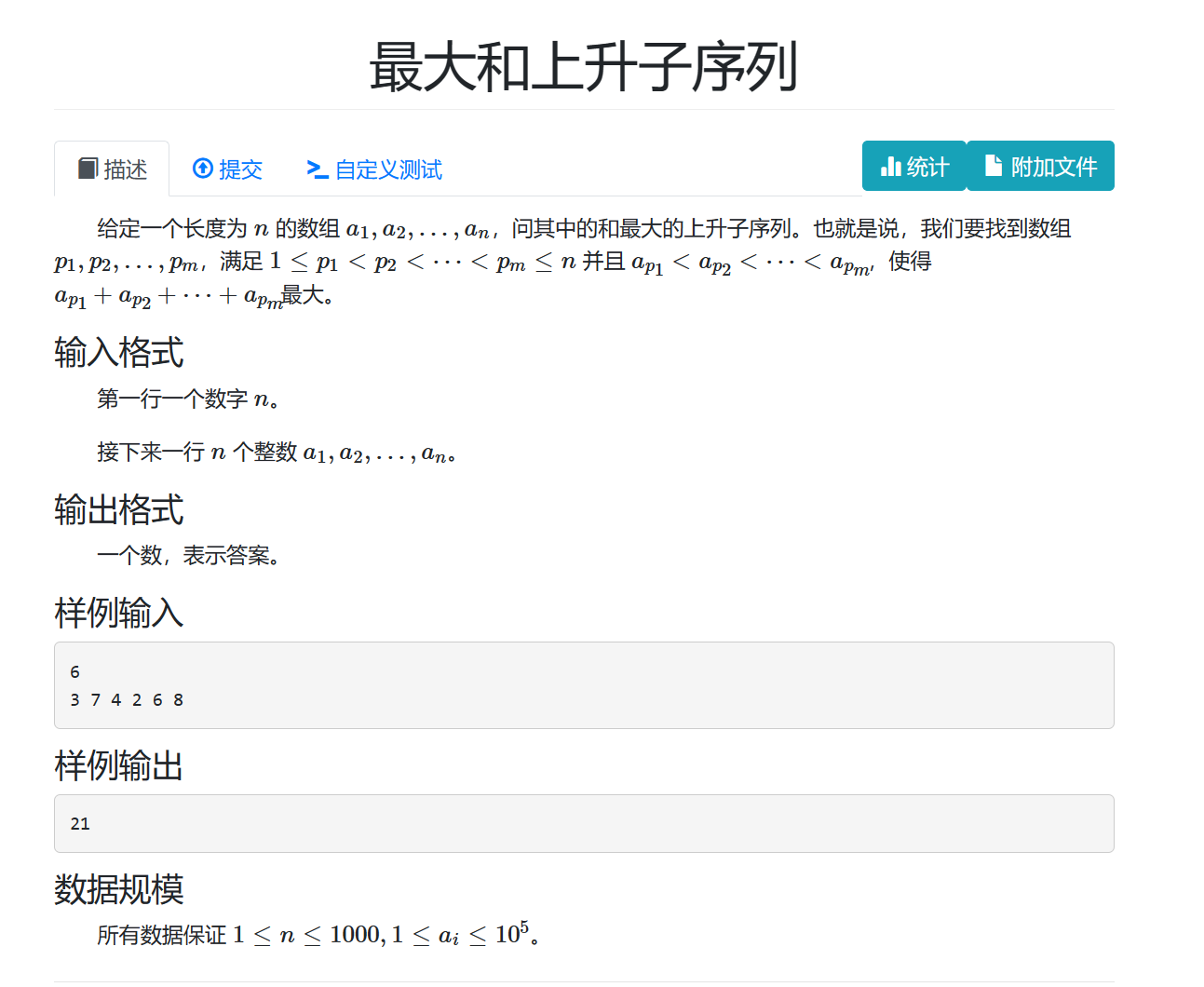
思路：dp，如果满足上升，那么比较较小数处当前值+较大数和较大数当前值即可。

#include<iostream>
#include<string.h>
#include<set>
#include<utility>
#include<queue>
using namespace std;
int n;
int f[1005];
long long a[100005];
int main()
{
    scanf("%d", &n);
    long long m = 0;
    for (int i = 0; i < n; i++)
    {
        scanf("%d", &f[i]);
        a[f[i]] = f[i];
    }
    for (int o = 0; o <n; o++)
    {
        for (int i = o+1; i < n; i++)
        {
            if (f[i] > f[o])
            {
                a[f[i]] = max(a[f[o]]+f[i],a[f[i]]);
                m = max(m, a[f[i]]);
            }
        }
    }
    printf("%lld", m);
    return 0;
}

T3

思路：先对每次操作后的每位数进行预处理，写出你、次操作后单一的该数字会变成几位数，最后根据预处理结果累加即可。

#include<iostream>
#include<string.h>
#include"stdio.h"
#include<queue>
using namespace std;
int main()
{
    int t;
    scanf("%d", &t);
    long long f[200050][10];
    for (int i = 0; i <= 9; i++)f[0][i] = 1;
    for (int i = 1; i <= 200010; i++)
    {
        for (int j = 1; j <= 9; j++)f[i][j - 1] = f[i - 1][j];
        f[i][9] = (f[i - 1][1] + f[i - 1][0]) % 1000000007;
    }
    for (int i = 0; i < t; i++)
    {
        int a[10] = { 0 };
        int m;
        char str[20];
        int res = 0;
        scanf("%s %d", &str, &m);
        int len = strlen(str);
        for (int i = 0; i < len; i++)
        {
            res += f[m][str[i] - '0'];
            res %= 1000000007;
        }
        printf("%d\n", res);
    }
    return 0;
}

T4

思路：将x轴方向和y轴的距离差除以最小公倍数后以pair的形式存入；最后放入set中去重；

#include<iostream>
#define _CRT_SECURE_NO_WARNINGS 1
#include<string.h>
#include<set>
#include<set>
#include<utility>
#include<queue>
using namespace std;
long long n, x[505], y[505];
long long gcd(long long  x, long long y)
{
    if (x < 0)x *= (-1);
    if (y < 0)y *= (-1);
    long long tmp;
    if (x < y)
    {
        tmp = x;
        x = y;
        y = tmp;
    }
    while (y>0)
    {
        tmp = x % y;
        x = y, y = tmp;
    }
    return x;
}
int main()
{
    long long ans = 0;
    cin>>n;
    set<pair<long long,long long>>s;
    int time;
    for (int i = 0; i < n; i++)
    {
        cin>>x[i] >> y[i];
    }
    for (int o = 0; o < n; o++)
    {
        for (int i = 0; i < n; i++)
        {
            if (i == o)continue;
            long long dx = x[o] - x[i];
            long long dy = y[o] - y[i];
            time = gcd(dx, dy);
            pair<long long, long long >p;
            p.first = dx / time;
            p.second = dy / time;
            if (!s.count(p))
            {
                ans++;
                s.insert(p);
            }

        }
    }
    cout << ans;
    return 0;
}

T5

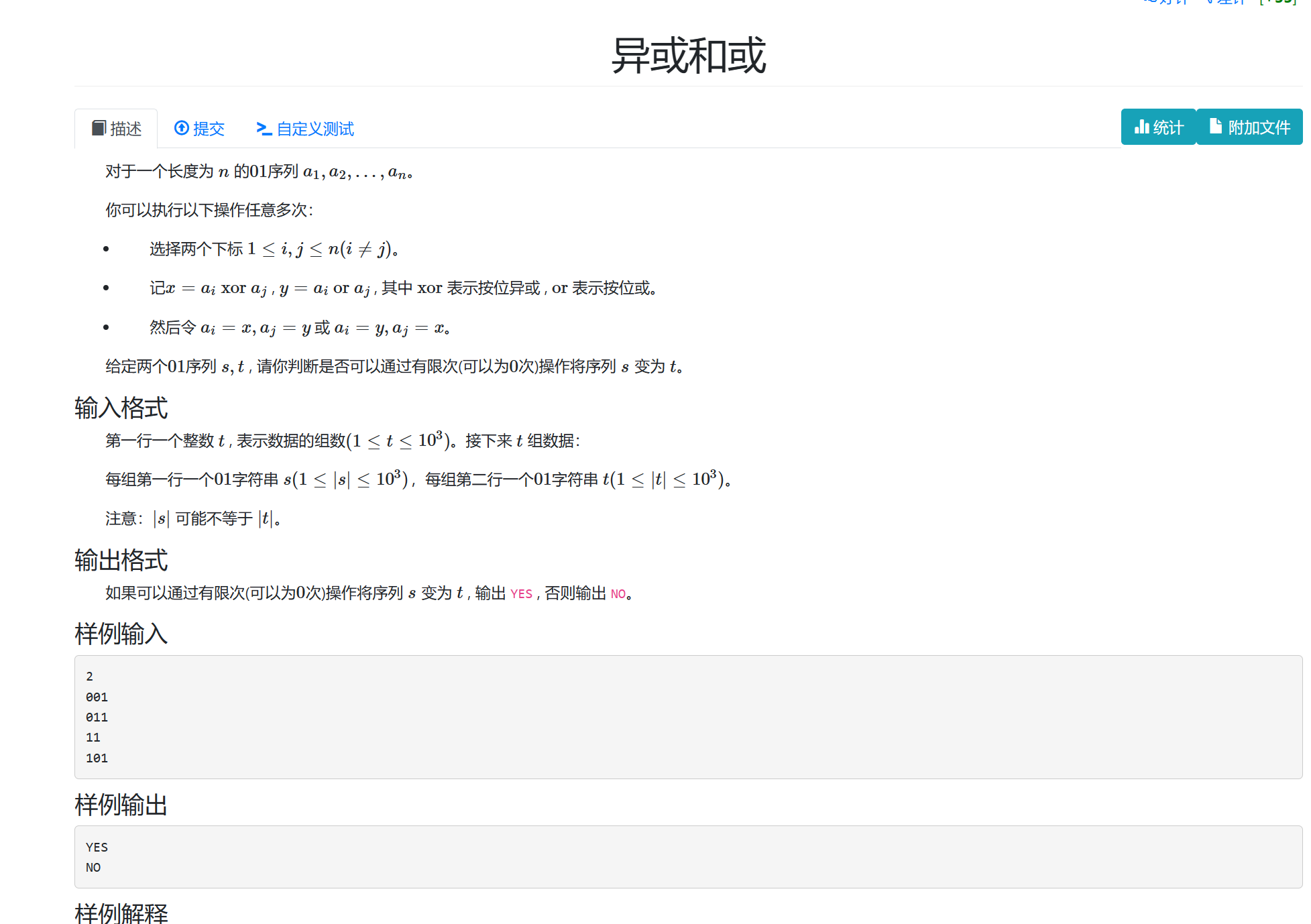
思路：

//0 1 --》1 1;

//0 0 --》0 0

//1 1 —》 0 1

#include<iostream>
#define _CRT_SECURE_NO_WARNINGS 1
#include<string.h>
#include<set>
#include<set>
#include<utility>
#include<queue>
using namespace std;
//0 1 :1 1;
//0 0 : 0 0
//1 1 : 0 1
int main()
{
    int t;
    cin>>t;
    for (int h = 0; h < t; h++)
    {
        string str1, str2;
        cin >> str1 >> str2;
        int len;
        if ((len=str1.length()) != str2.length())
        {
            cout << "NO\n";
            continue;
        }
        if (str1 == str2)
        {
            cout << "YES\n";
            continue;
        }
        bool siu = 0;
        int tmp;
        for (int i = 0; i < len; i++)
            {
                if (str1[i] == '1')
                {
                    siu = 1;
                    tmp = i;
                    break;
                }
            }
        if (str1[tmp] == str2[tmp])
        {
            cout << "YES\n";
            continue;
        }
        bool qq = 0;
        for (int i = 0; i < len; i++)
        {
            if (str2[i] == '1' && i != tmp)
            {
                cout << "YES\n";
                qq = 1;
                break;
            }
        }
        if (qq == 0)cout << "NO\n";

    }
    return 0;
}

T6

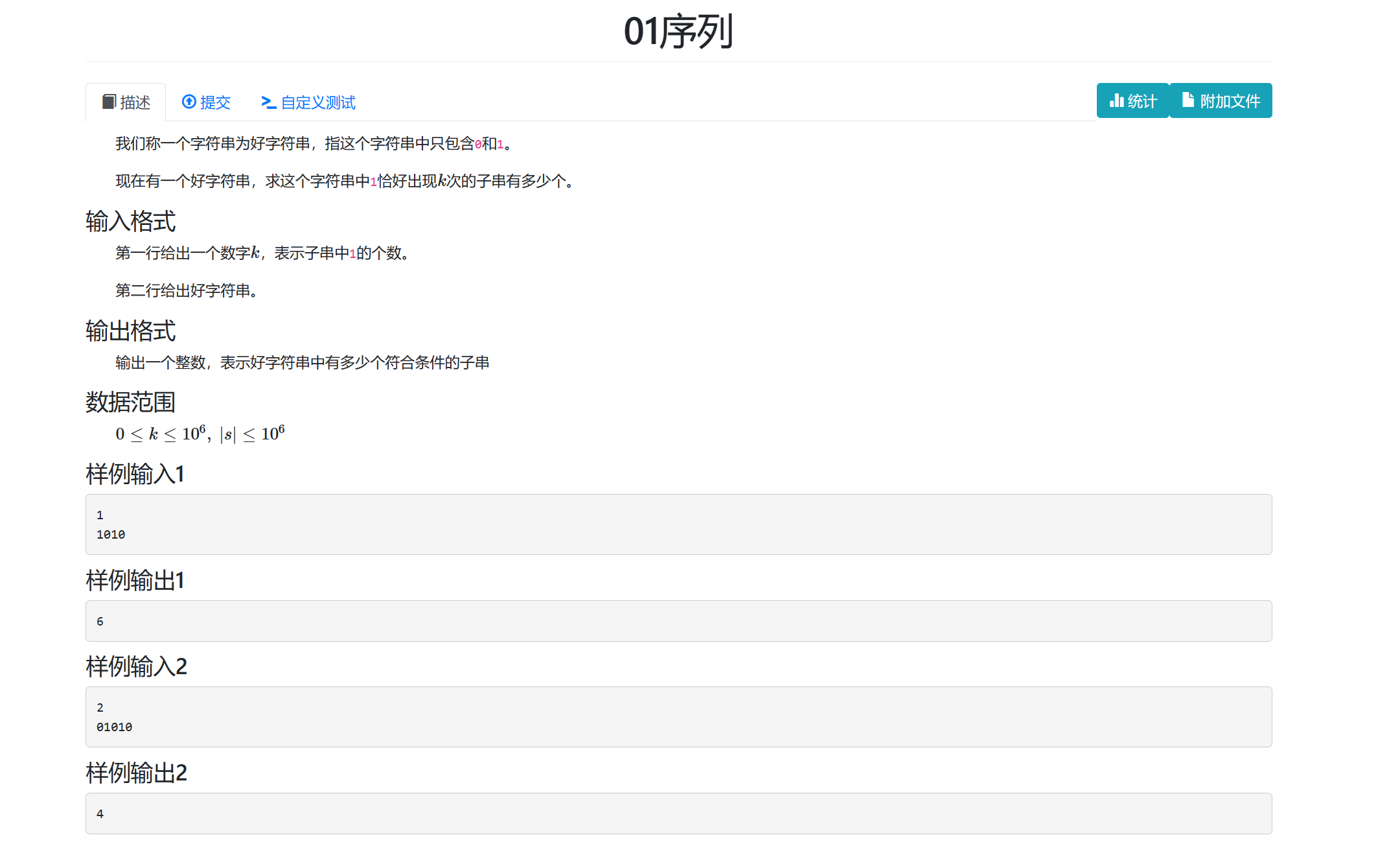
思路：将连续的零的个数存入一个一维数组，这样结果就为数组中下标相差k的两组连续零的个数分别加一后的乘积的累加

#include<iostream>
#define _CRT_SECURE_NO_WARNINGS 1
#include<string.h>
#include<set>
#include<set>
#include<utility>
#include<queue>
using namespace std;

int main()
{
    int k;
    cin >> k;
    int a[1000005]={ 0 };
    string str;
    cin >> str;
    long long len = str.length(),ans=0,res=0;
    int cnt = 0;
    int tot = 0;
    if (k == 0)
    {
        for (long long i = 0; i <= len; i++)
        {
            if (str[i] == '0')ans++;
            else
            {
                res += (ans * (ans + 1)) / 2;
                ans = 0;
            }
        }
        cout << res;
        return 0;
    }
    for (int i = 0; i < len; i++)
    {
        if (str[i] == '0')
        {
            a[cnt]++;
        }
        else cnt++;
    }
    for (int i = k; i <= cnt; i++)
    {
        res += (a[i]+1) * (a[i - k]+1);    
    }
    cout << res;
    return 0;
    
}

T7

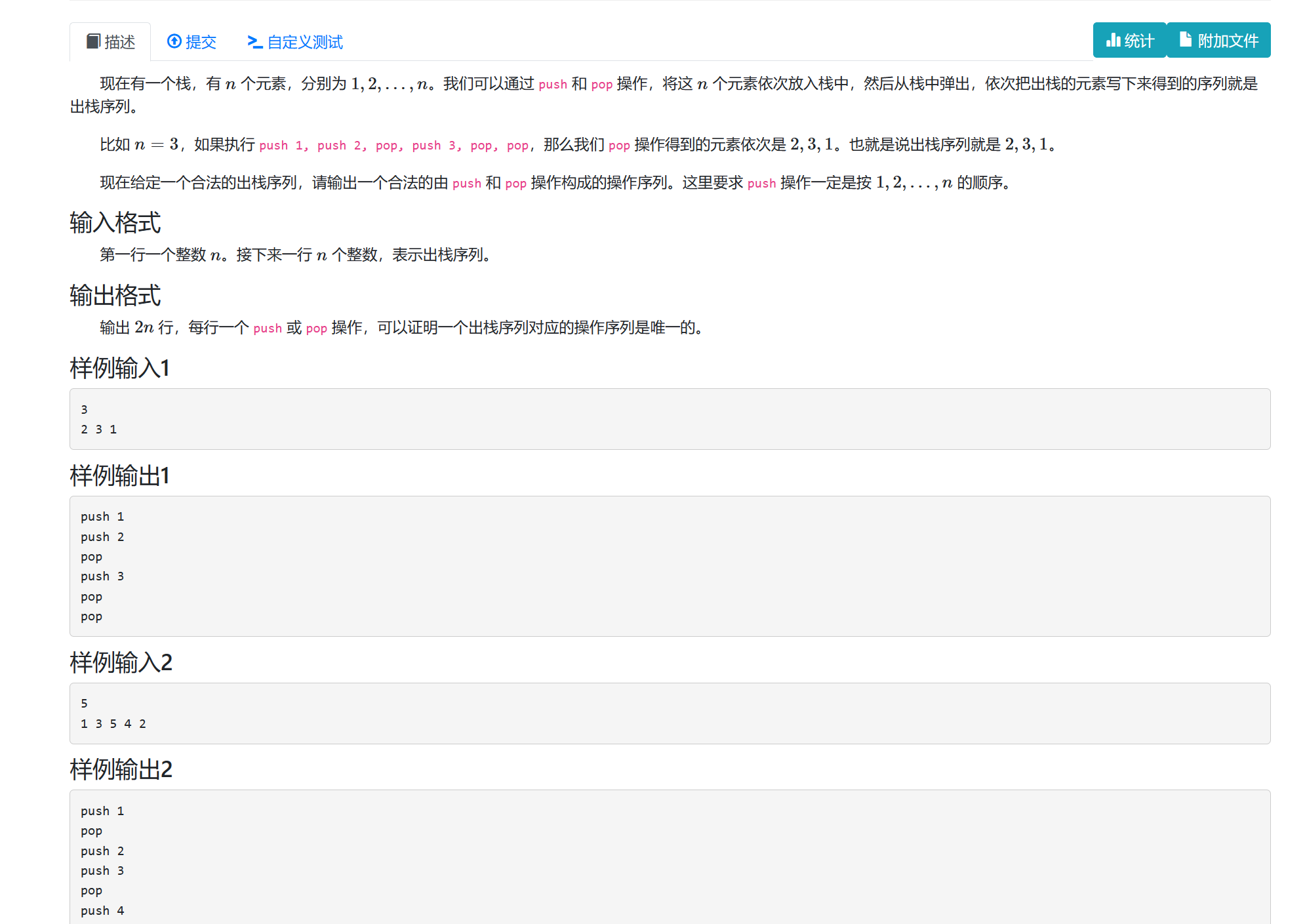
栈中元素单调增，所以如果栈顶元素小于需弹出的元素，则需继续push，若相等，则pop

#include<iostream>
#define _CRT_SECURE_NO_WARNINGS 1
#include<string.h>
#include<set>
#include<set>
#include<utility>
#include<stack>
#include<queue>
using namespace std;
int a[100005];
stack<int> num;
int main()
{
    int n;
    cin >> n;
    for (int i = 1; i <= n; i++)
    {
        scanf("%d", &a[i]);
    }
    num.push(-1);
    int cnt = 0;
    for (int i = 1; i <= n; i++)
    {
        if (num.top() == a[i])
        {
            printf("pop\n");
            num.pop();
            continue;
        }
        int k = i;
        while (num.top() < a[i])
        {
            printf("push %d\n", ++cnt);//cout << "push " << ++cnt << endl;
            num.push(cnt);
        }
        printf("pop\n");//cout << "pop\n";
        num.pop();
    }


    return 0;
}

T8

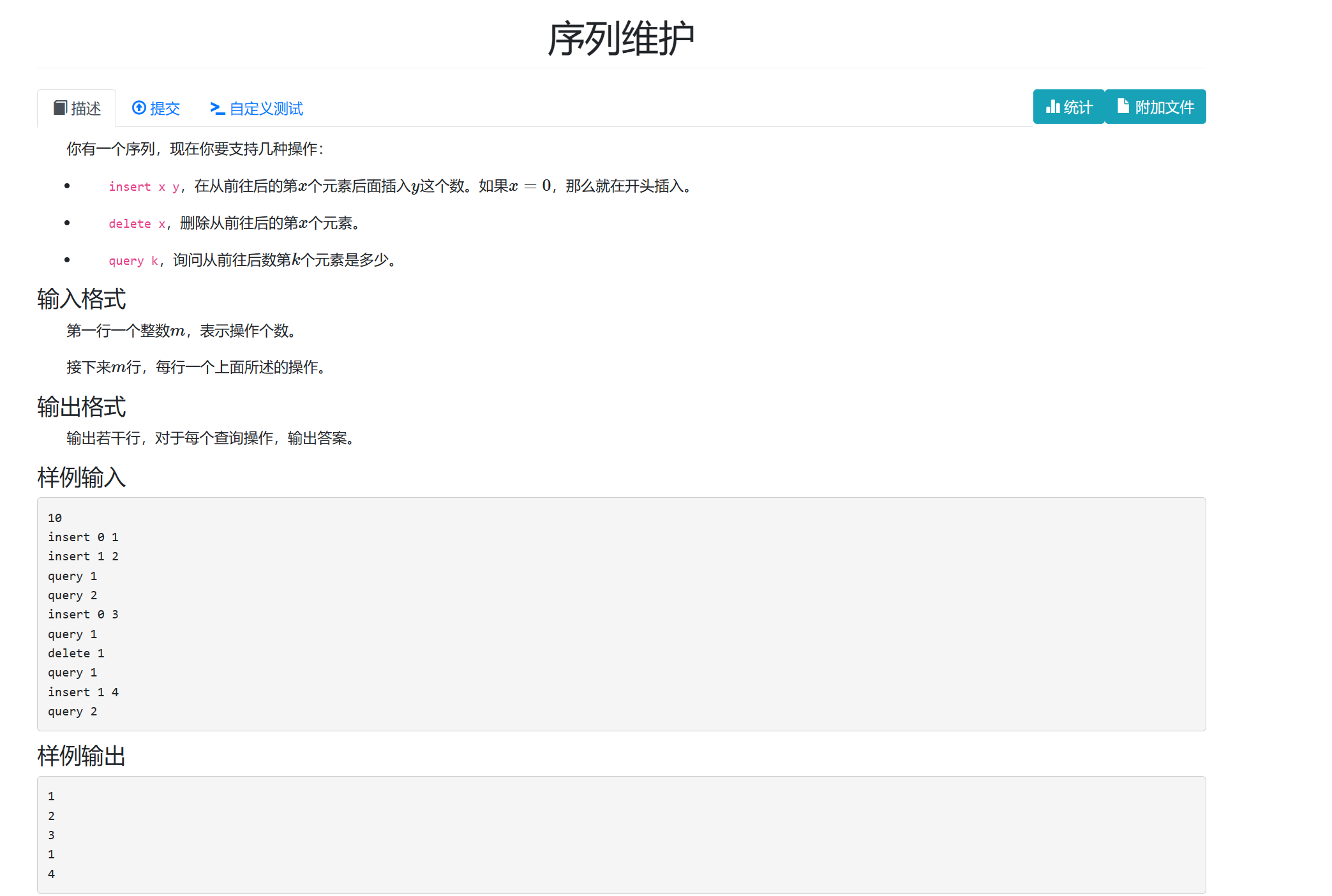
思路：考察vector的使用

#include<iostream>
#define _CRT_SECURE_NO_WARNINGS 1
#include<string.h>
#include<set>
#include<set>
#include<utility>
#include<stack>
#include<queue>
#include<vector>
using namespace std;
int main()
{
    vector<int>c;
    string op;
    int m;
    scanf("%d", &m);
    int x, y, k;
    for (int z = 0; z < m; z++)
    {
        scanf("%s",&op);
        if (op == "insert")
        {
            scanf("%d %d", &x, &y);//cin >> x >> y;
            c.insert(c.begin() + x, y);
        }
        else if (op == "delete")
        {
            scanf("%d", &x);//cin >> x;
            c.erase (c.begin()+x-1);
        }
        else 
        {
            scanf("%d", &k);//cin >> k;
            cout << c[k - 1]<<endl;
        }
    }


    return 0;
}

T9

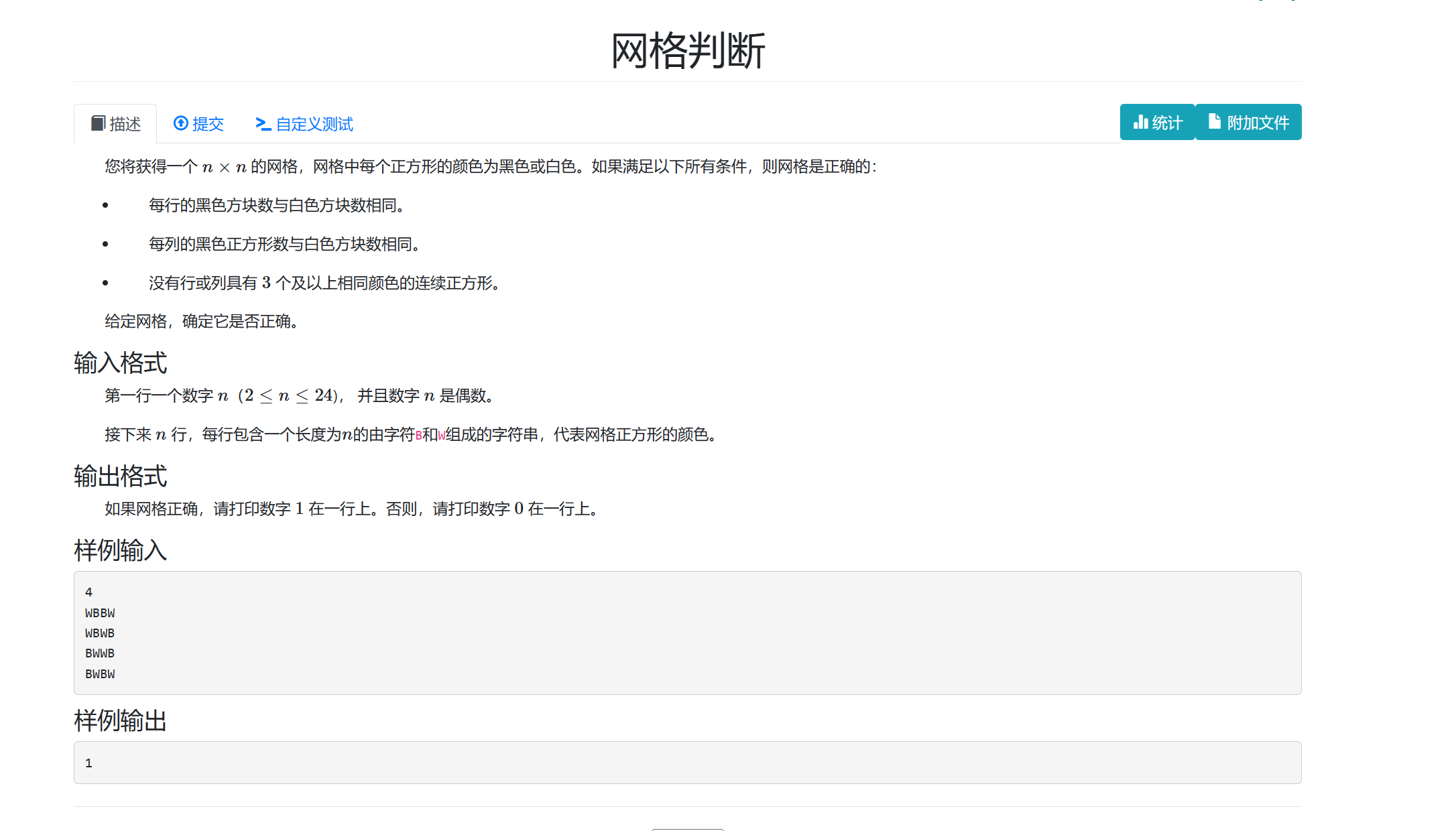
需要记录输入到某个位置时，该行与该列之前的是什么颜色，如果相同，计数器加，如果不同，更新颜色，计数器化一。

#include<iostream>
#define _CRT_SECURE_NO_WARNINGS 1
#include<string.h>
#include<set>
#include<set>
#include<utility>
#include<stack>
#include<queue>
#include<vector>
using namespace std;
int main()
{
    int n;
    cin >> n;
    int hb[27] = { 0 }, hw[27] = { 0 }, lb[27] = { 0 }, lw[27] = { 0 };
    char c[27][27];
    int cnth = 0, cntl[27] = {0};
    char preh, prel[27];
    for (int h = 0; h < n; h++)
    {
        for (int i = 0; i < n; i++)
        {
            cin >> c[h][i];
        }
        prel[h] = 'q';
    }
    for (int h = 0; h < n; h++)
    {
        preh = 'q';
        for (int i = 0; i < n; i++)
        {
            if (c[h][i] == 'W')
            {
                hw[h]++;
                lw[i]++;
            }
            else
            {
                hb[h]++;
                lb[i]++;
            }

            if (c[h][i] == preh)
            {
                cnth++;
            }
            else
            {
                if (cnth >= 3)
                {
                    cout << "0";
                    return 0;
                }
                cnth = 1;
                preh = c[h][i];
            }

            if (c[h][i] == prel[i])
            {
                cntl[i]++;
                if (cntl[i] == 3)
                {
                    cout << "0";
                    return 0;
                }
            }
            else
            {
                cntl[i] = 1;
                prel[i] = c[h][i];
            }

        }
    }
    for (int i = 0; i < n; i++)
    {
        if (hw[i] != hb[i] || lw[i] != lb[i])
        {
            cout << '0';
            return 0;
        }
    }
    cout << '1';
    return 0;
}

T10

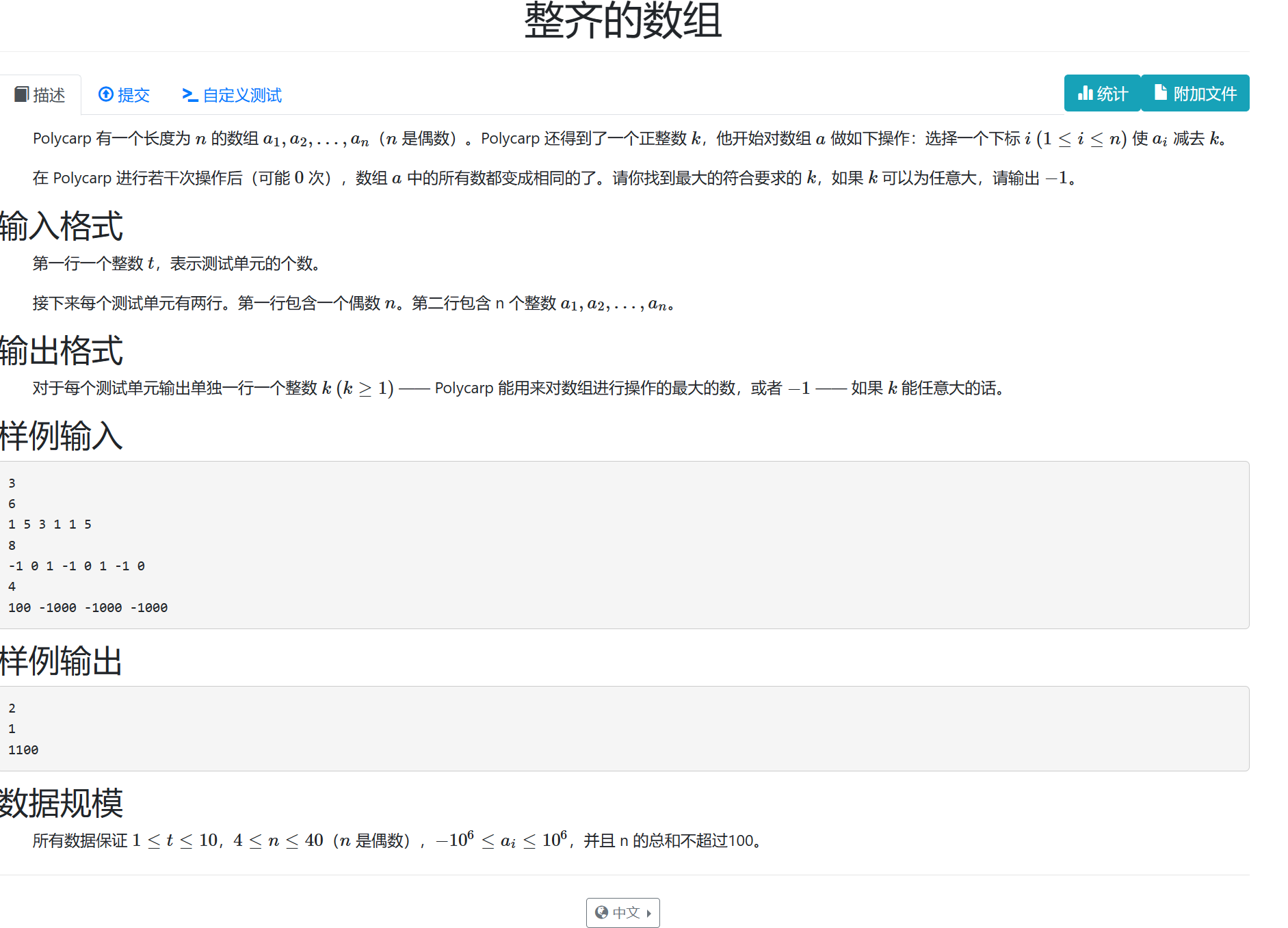
思路：

先用set去重、排序，然后用一维数组取出，定义gcd函数找出两个数的最大公约数，之后用每个数与最小的那个数的差值与之前的最大公约数再求一次最大公约数即可。

#include<iostream>
#define _CRT_SECURE_NO_WARNINGS 1
#include<string.h>
#include<set>
#include<set>
#include<utility>
#include<stack>
#include<queue>
#include<vector>
using namespace std;
int gcd(int x, int y)
{
    if (x < 0)x *= (-1);
    if (y < 0)y *= (-1);
    int tmp;
    if (x < y)
    {
        tmp = x; x = y; y = tmp;
    }
    while (y > 0)
    {
        tmp = x % y;
        x = y;
        y = tmp;
    }
    return x;
}
int main()
{
    int t;
    cin >> t;
    for (int qq = 0; qq < t; qq++)
    {
        set<int> s;
        int tmp, n;
        cin >> n;
        for (int wx = 0; wx < n; wx++)
        {
            cin >> tmp;
            s.insert(tmp);
        }
        if (s.size() == 1)
        {
            cout << "-1";
            continue;
        }
        int num[105],cnt=0;
        for (auto it = s.begin(); it != s.end(); it++)
        {
            num[cnt++] = *it;
        }

        set<int> c;
    
            for (int i = 1; i < cnt; i++)
            {
                num[i] -= num[0];
            }
            for (int i = 2; i < cnt; i++)
            {
                num[i] = gcd(num[i], num[i - 1]);
            }
            cout << num[cnt - 1] << endl;


    }

    return 0;
}

AC-MAN
关注
【LeetCode】【算法】160.相交链表
passer__jw767的博客
11-05 368
Leetcode 160. 相交链表
二分查找习题篇(上)
zoelinkailuo的博客
11-07 948
给定⼀个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。这里，我们把数组的元素分为两部分——小于等于target的部分[left,Bright] and 大于target的部分[Bright+1,right]。这里，我们把数组的元素分为两部分——平方后小于等于x的部分[1,mid] and 平方后大于x的部分[mid-1, x]和一个目标值，在数组中找到目标值，并返回其索引;
GJ Round (2024.10) Round 8~21
lunjiahao的博客
11-06 865
前言： 点此 返回 GJ Round 目录 Round 8 (10.5) A 给定 nnn 个区间，每个区间 [li,ri][l_i,r_i][li​,ri​]，最大化选取区间对数，使得每对区间 [li,ri],[lj,rj][l_i,r_i],[l_j,r_j][li​,ri​],[lj​,rj​] 满足 [li,ri]∩[lj,rj]=∅[l_i,r_i] \cap [l_j,r_j] =\varnothing[li​,ri​]∩[lj​,rj​]=∅ 先按 lil_ili​ 从小到大排序，再按
【刷题】优选算法
林宇恒的博客
11-06 484
如图，我们先算出最左边(1)和最右边(7)围起来的容量，然后，7不动，1继续和7的左边3，8，4...遍历算出容量，你会发现底是不断缩短的，同时高一直都是1，因为高只有两种情况，比它小或和它相等，所以1和7左边的值算出来的容量都是比1和7的容量小的，因为底在不断变小同时高可能不变也可能变小。根据两个实例和鸽巢原理可以发现不断的平方和最终都会形成环，所以我们可以联想到用快慢指针，慢指针走一步，快指针走两步，最终会在环相遇，判断相遇时是否为1。第一个实例是快乐数，因为会变为1且不断是1的循环。
【LeetCode】【算法】416. 分割等和子集
passer__jw767的博客
11-06 312
LeetCode 416. 分割等和子集
69. x 的平方根
学习历程记录和分享
11-06 183
注意：不允许使用任何内置指数函数和算符，例如 pow(x, 0.5) 或者 x ** 0.5。由于返回类型是整数，结果只保留 整数部分 ，小数部分将被 舍去。给你一个非负整数 x ，计算并返回 x 的 算术平方根。
算法通关（4）-- 前缀树
2301_79985750的博客
11-07 996
前缀树（Trie树），也称为字典树，是一种用于的数据结构。它是一种树形结构，能够利用字符串的公共前缀来减少存储空间和查询时间。现在有“acb”,"cba","acc"，"ac"四个字符串，利用这四个字符串构出一颗前缀树。根节点不包含任何字符，是所有字符串的公共前缀；每个节点包含pass信息，代表加节点的时候路过了几次，还有一个end信息表示多少个字符串是以当前字符串结尾的。举个例子：插入完成后得到的树形结构：那么现在问：字符串acb出现了几次。
2024年华为OD机试真题-矩阵扩散-Java-OD统一考试（E卷）
面试高手的博客
11-06 188
时间复杂度为O(m * n)，因为每个点最多会被访问一次，每次访问时会扩展到它的邻居点，所有的扩展过程一共涉及m×n个点。- 当队列为空时，表示矩阵中所有点都已经被扩散，这时输出最大的扩散时间，即为整个矩阵所有点变为1所需的时间。- 使用一个二维数组dist来记录每个点的扩散时间，初始时所有点的时间设为-1，表示未被访问。- 如果邻居点未被访问（时间为-1），则将其扩散为1，并将该点的时间设为当前点的时间+1。- 我们从两个扩散点同时开始扩散，将其周围为0的点转化为1，并逐步向外扩展。
人脸识别技术：从算法到深度学习的全面解析
梵心白莲的博客
11-07 1034
人脸识别技术作为一种重要的生物识别技术，在当今社会中具有举足轻重的地位。它广泛应用于各个领域，如金融领域的实名认证、安保领域的门禁系统、通行领域的火车站和地铁站检票、泛娱乐领域的美颜相机和短视频特效处理、公安和司法领域的逃犯追捕和服刑人员管理、自助服务设备以及考勤和会务等。
贪心算法day3（最长递增序列问题）
2301_80785428的博客
11-08 352
思路：我们只需要设置两个数进行比较就好。设a为nums[0]，b 为一个无穷大的数，只要有比a小的数字就赋值a，比a大的数字就赋值b，如果有比b大的数字说明可以组成一个三元子序列直接返回true。
01背包模板+空间压缩优化
aoe_z的博客
11-06 948
01背包模板+空间压缩优化01背包模板。
xtu oj 数字
最新发布
夜空像是一片紫水潭，星星是些不动的大亮点，夜风是些浅蓝色的流线，云端传来喧嚣的声音。
11-10 692
枚举个位数字就能知道能不能被 10 整除了
置信传播算法复现
程序猿追的博客
11-08 106
例如，许多其他资源分配、调度安排、路径规划等问题在本质上与0 - 1背包问题有相似之处，通过对0 - 1背包问题的研究，可以探索通用的求解策略和近似算法，用于解决更广泛的NP难问题。例如，一家电子产品制造企业有一定数量的芯片、电路板等原材料，以及有限的生产线使用时间，要决定生产哪些型号的电子产品（每个型号产品视为一个物品，其价值为利润，重量为所需资源量），从而在不超过资源限制的情况下获得最大利润。载重约束为因子图中的一个因子节点，每个物品的状态约束为一个子句节点，变量节点与包含该变量的子句节点相连。
利用dem和DOM生成路线算法的实现
llhllq2015的博客
11-08 749
DEMProcessor类：加载DEM数据，并提供 isObstacle 方法，用于检测高度是否超过指定阈值（作为障碍物）。规避DEM中的地物：利用DEM的高度数据识别障碍物，如山体、水域等不可通行区域，并设计路径绕过它们。VectorExporter类：将生成的路径导出为GeoJSON格式，方便后续的GIS分析。判断DOM中的地物：结合DOM数据对地物进行分类和识别，如道路、建筑、植被等。生成连续的线路图：基于路径算法生成起点到终点的连续路径线。主程序：加载DEM，生成路径并导出矢量数据。
100种算法【Python版】第53篇——无损压缩之LZW算法
AnFany
11-06 108
100种算法【Python版】第53篇——无损压缩之LZW算法
力扣排序455题（分发饼干）
HandsomeBoyqxc的博客
11-07 398
代码：
【数据结构和算法】五、贪心算法原理讲解的实战演练
weixin_45736855的博客
11-07 965
贪心算法的原理、思路介绍
【LeetCode】【算法】208. 实现 Trie (前缀树)
passer__jw767的博客
11-06 319
LeetCode 208. 实现 Trie (前缀树)
977.有序数组的平方
qq_69304031的博客
11-07 356
平方后，数组变为 [16,1,0,9,100]排序后，数组变为 [0,1,9,16,100]组成的新数组，要求也按。
打印沙漏的4种解法（直接法编程、艺术化编程）
tn1949的博客
11-09 724
在前几个做法中，我们是一行一行打印字符串来做，但如果我们整体来看，就是一个图案，不把它当成字符组成的，而是一个二维坐标系。针对这道题，我们就是一行行打印字符串，并且发现行与行之间的规律是等差数列。我们只需知道最大行的字符数或总列数，便可以通过循环，分为上下两部分来解决问题解决这道问题。本题要求你写个程序把给定的符号打印成沙漏的形状。这道题，前三种方法完全可以，但艺术化编程就会出现格式化问题，可以自己去试试为什么。首先打印出由给定符号组成的最大的沙漏形状，最后在一行中输出剩下没用掉的符号数。
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值