如果说信息是思想,消息是语言的话,那么信号就是声音。思想通过语言来表达,语言通过声音来传输,这就是信号与信息、消息之间的关系。
信号是通信系统中看得见、摸得着的东西,是通信系统直接处理的对象,因此,了解信号的一些概念和分析方法,是了解通信系统、通信产品的工作原理的基础。
信号的“相貌”特征
信号的定义在数学上可以表示为一个或多个变量的函数。
通信中的信号,基本上是时间的函数。
信号从发生到传输再到被接收,还是不是原来的模样,这是能否成功通信的关键。
强度、频率、相位、能量等是信号的基本特征,也是我们分析信号和系统的基础。下面通过一个简单的信号来了解一下信号的这些特征。
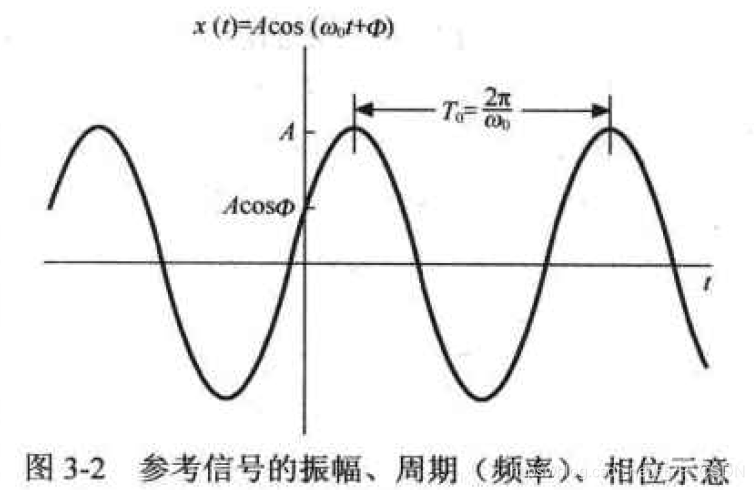
如果钟摆底端带有墨汁,在一张纸上匀速通过,那么钟摆所画下的运动轨迹是正弦信号的波形图。
正弦信号一般是用三角余弦函数来表示的:
x
(
t
)
=
A
cos
(
ω
0
t
+
ϕ
)
x(t)=A\cos(\omega_0t+\phi)
x(t)=Acos(ω0t+ϕ)
其中
A
A
A表示最大振幅,也就是钟摆最大的摆动幅度;
ω
0
\omega_0
ω0为角速度,表示为
ω
0
=
2
π
/
T
\omega_0 = 2\pi/T
ω0=2π/T,
T
T
T是这个信号的周期,两个波峰的间隔即为一个周期。因为周期和频率是反比关系,周期的倒数等于频率
f
0
f_0
f0,所以
ω
0
=
2
π
f
0
\omega_0 = 2\pi f_0
ω0=2πf0,这把
ω
0
\omega_0
ω0与频率等同起来了,见到
ω
0
\omega_0
ω0,要想到这是信号的频率。
(
ω
0
t
+
ϕ
)
(\omega_0t+\phi)
(ω0t+ϕ)称为信号的相位,
ϕ
\phi
ϕ称为信号的初始相位,即在初始时刻的相位。
钟摆所揭示的这种震荡规律在电路也有。无线通信中调制用的载波,就是正弦波,这说明正弦波是可以由电路来产生的,这样的电路也称为正弦波振荡器。
信号的“个性”——频谱
正弦波的作用:
- 作为调制的载波。
- 由于它比较简单,人们对它也很熟悉,因此常被用来作为研究系统的参考信号。
- 在遇到较为复杂的信号时,也可以靠它来化繁为简,将复杂信号分解为正弦信号来表示。
一个复杂的周期信号,可以分解为不同频率的正弦信号的叠加,用下面关系式来表示这种叠加。
x
(
t
)
=
A
0
/
2
+
A
1
cos
(
ω
0
t
)
+
B
1
sin
(
ω
0
t
)
+
A
2
cos
(
2
ω
0
t
)
+
B
2
sin
(
2
ω
0
t
)
+
.
.
.
+
A
k
cos
(
k
ω
0
t
)
+
B
k
sin
(
k
ω
0
t
)
+
.
.
.
x(t) = A_0/2 + A_1\cos(\omega_0 t) + B_1\sin(\omega_0t) + A_2\cos(2\omega_0 t) + B_2\sin(2\omega_0t) + ... + A_k\cos(k\omega_0 t) + B_k\sin(k\omega_0t) + ...
x(t)=A0/2+A1cos(ω0t)+B1sin(ω0t)+A2cos(2ω0t)+B2sin(2ω0t)+...+Akcos(kω0t)+Bksin(kω0t)+...
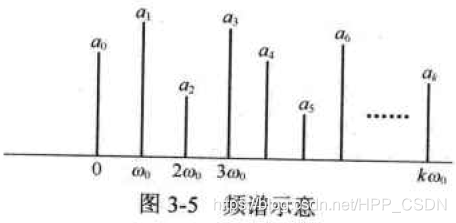
这里边,所有正弦信号分量的频率都是 ω 0 \omega_0 ω0的整数倍,因此将 ω 0 \omega_0 ω0称为基波,将 k ω 0 k\omega_0 kω0称为 k k k次谐波。
因为复指数函数和三角函数密切相关,具有
e
j
ω
t
=
cos
ω
t
+
j
sin
ω
t
e^{j\omega t} = \cos \omega t + j\sin \omega t
ejωt=cosωt+jsinωt 的等式,所以一般又将上式改造成更方便的复指数形式。
x
(
t
)
=
a
0
+
a
1
e
j
ω
0
t
+
a
2
e
j
2
ω
0
t
+
.
.
.
+
a
k
e
j
k
ω
0
t
+
.
.
.
=
∑
k
=
−
∞
+
∞
a
1
e
j
k
ω
0
t
(3-2)
x(t) = a_0 + a_1e^{j\omega_0 t} + a_2e^{j2\omega_0 t} + ... + a_ke^{jk\omega_0 t} + ... = \sum_{k=-\infty}^{+\infty}a_1e^{jk\omega_0 t} \tag{3-2}
x(t)=a0+a1ejω0t+a2ej2ω0t+...+akejkω0t+...=k=−∞∑+∞a1ejkω0t(3-2)
这个关系式也称为周期信号的傅里叶级数,以 ω 0 \omega_0 ω0为基波,谐波频率逐级加大,所以叫级数。其中的 a 0 , a 1 , a 2 , . . . , a k , . . . a_0,a_1,a_2,...,a_k,... a0,a1,a2,...,ak,...是各次谐波的幅度,也称为信号 x ( t ) x(t) x(t)的频谱系数。频谱系数表示各频率分量在总信号中所占的分量。
将频谱系数和频率分量对应起来,画到一张纸上,就可以直观地看出每个频率分量的强度,如图3-5所示,这个图也称为信号的频谱图。
信号是时间的函数,所以信号是连续的还是离散的,要看信号在时间上的取值是连续的还是离散的。
信号函数在时间的连续值上都有定义就称为连续时间信号,而如果仅仅在离散时间点上有定义的话则称为离散时间信号。
通常,在信号的数学描述上,用 ( t ) (t) (t) 表示连续时间信号,用 [ n ] [n] [n] 表示离散时间信号。
从周期信号的傅里叶级数看到,周期信号的频谱是离散的,但周期信号并不一定是离散的。
非周期信号的频谱是连续的。傅里叶认为将周期信号的周期无限扩大就是非周期信号,故非周期信号也可以分解为正弦信号叠加。傅里叶创立了影响深远的傅里叶变换和反变换公式,使信号既可以在时域中分析,还可以在频域中分析。
将周期无限扩大后,傅里叶级数该如何表示?
频率和周期是反比的关系,周期无限扩大,那频率间隔就要无限地缩小,逼近连续了,如图3-8所示。
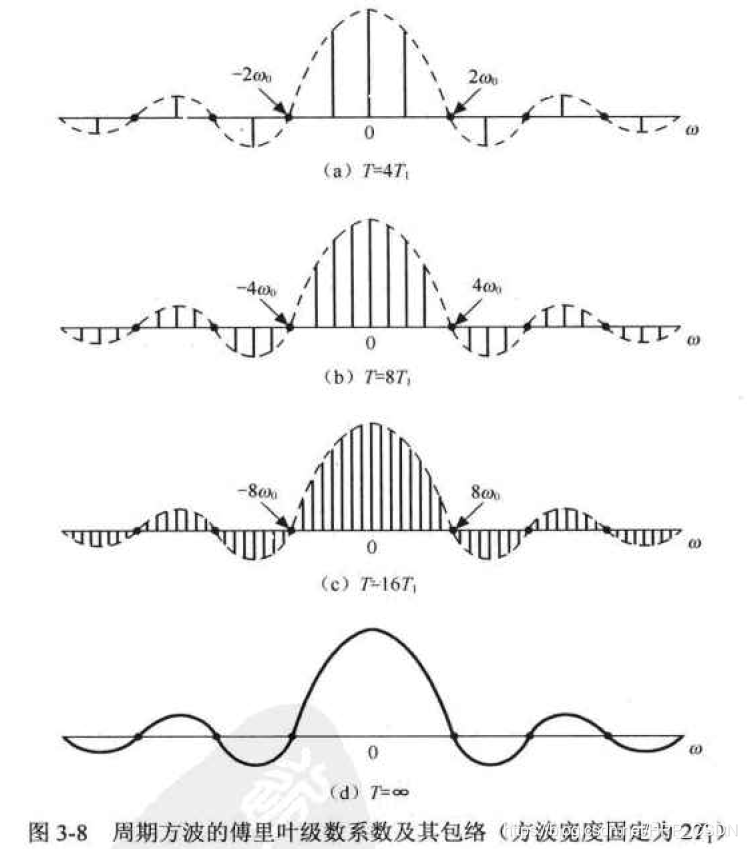
这种逼近连续的叠加,在数学上需要用积分来表示。
积分是一种特殊的叠加,比如说求一个不规则图形的面积,先要分解为规则的图形分别求面积,最后将这些规则图形的面积相加,分得越细,求解越精确。
积分的意义就是把对象分得无限小再求和。分的过程叫微风,加的过程叫积分。
现在把周期信号的傅里叶级数改造为非周期信号的傅里叶级数,把求和符号
∑
\sum
∑用积分符号
∫
d
x
\int dx
∫dx代替,再对变量做相应的修改。
f
(
t
)
=
1
2
π
∫
−
∞
+
∞
F
(
ω
)
e
j
ω
t
d
ω
(3-3)
f(t) = \frac{1}{2\pi} \int_{-\infty}^{+\infty}F(\omega)e^{j\omega t} d\omega \tag{3-3}
f(t)=2π1∫−∞+∞F(ω)ejωtdω(3-3)
此式的 F ( ω ) F(\omega) F(ω)相当于式(3-2)的 a k a_k ak (频谱系数)。实际上, a k a_k ak和 F ( ω ) F(\omega) F(ω)的计算公式也相似。
a
k
=
1
T
∫
T
x
(
t
)
e
−
j
k
ω
0
t
d
t
(3-4)
a_k = \frac{1}{T}\int_T x(t) e^{-jk\omega_0t}dt \tag{3-4}
ak=T1∫Tx(t)e−jkω0tdt(3-4)
F
(
ω
)
=
∫
−
∞
+
∞
e
−
j
ω
t
d
t
(3-5)
F(\omega) = \int_{-\infty}^{+\infty}e^{-j\omega t}dt \tag{3-5}
F(ω)=∫−∞+∞e−jωtdt(3-5)
从信号的时间函数求信号的频谱称为傅里叶变换 (式3-5),从信号的频谱求解信号的时间函数称为傅里叶反变换 (式3-3)。
通过频谱分析信号的幅度与相位以及频率之间的关系也称为频域分析,分析信号的幅度与时间的关系也称为时域分析。
要对一个时间信号进行频域分析,就得先应用傅里叶频谱系数公式 (式3-4) 或傅里叶变换公式求出它的频谱来。
正弦信号、方波信号和周期冲激串是通信系统中常会用到的信号。正弦信号往往作为无线通信的载波出现,方波是大多数数字信号的波形,而冲激串可以作为采样信号,在模拟信号转换为数字信号的过程中扮演着重要的角色。
正弦信号可以用余弦三角函数和正弦三角函数来表示。不同的函数表示不同的频谱。
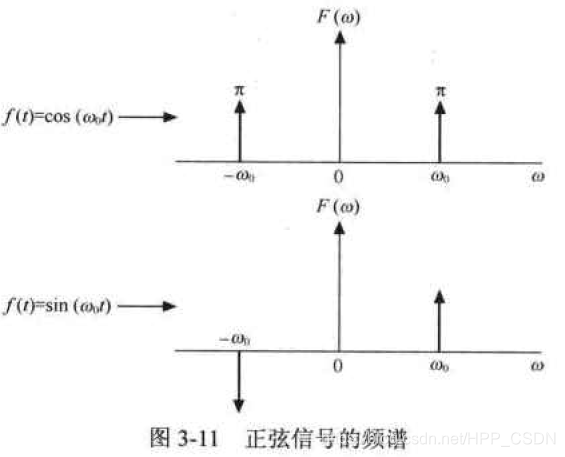
用正弦三角函数表示的信号的频谱与余弦三角函数表示的信号的频谱,有一边是相反的。
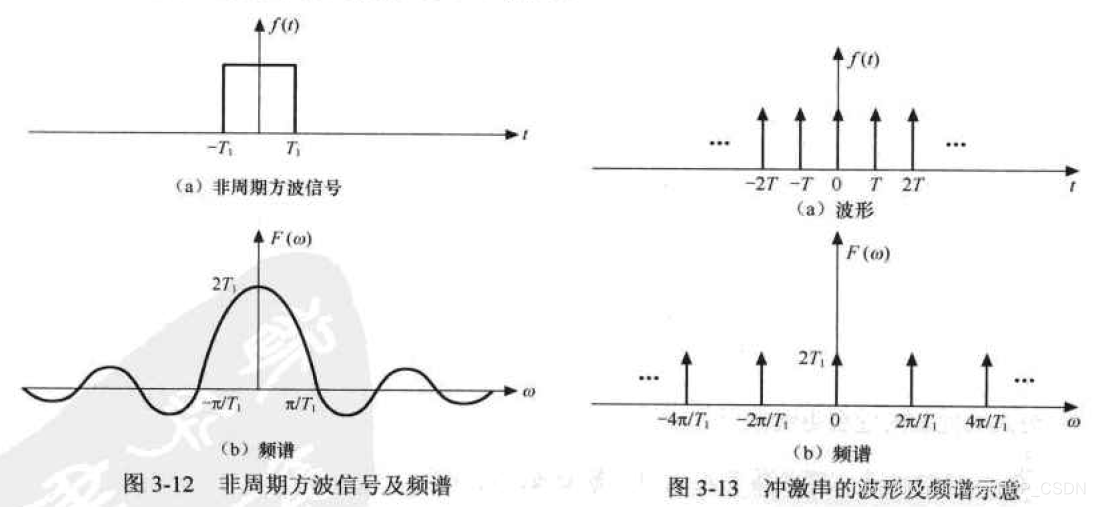
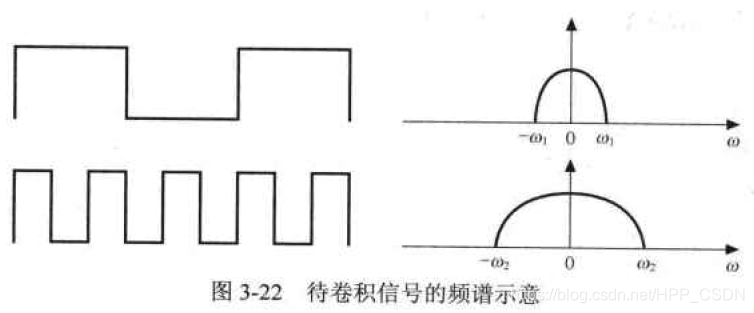
非周期方波的频谱如图3-12所示。冲激串的波形的频谱如图3-13所示。
信号的“游戏”——卷积
如果两个信号相乘,要想得到相乘后的频谱,不能直接将其频谱相乘,也不需先在时域中计算信号的相乘结果,再利用傅里叶变换来求得相乘后的频谱。
时域中相乘的两个信号,在频域中可以通过卷积来求得相乘后的频谱。
卷积是一种运算的方法,来源于信号通过线性系统后的响应。
y
[
n
]
=
∑
k
=
−
∞
+
∞
x
[
k
]
h
[
n
−
k
]
(3-6)
y[n] = \sum_{k=-\infty}^{+\infty} x[k]h[n-k] \tag{3-6}
y[n]=k=−∞∑+∞x[k]h[n−k](3-6)
表达式 3-6 的物理意义是将其中一个信号 h [ n ] h[n] h[n]沿 k k k移位 ( h [ n − k ] h[n-k] h[n−k]),再与另一个信号 x [ n ] x[n] x[n]相乘,然后求和叠加。这个运算就称为信号 x [ n ] x[n] x[n]和信号 h [ n ] h[n] h[n]的卷积,记作: y [ n ] = x [ n ] ∗ h [ n ] y[n]=x[n]*h[n] y[n]=x[n]∗h[n],两个信号中间的 ∗ * ∗表示卷积。
假设
x
[
n
]
x[n]
x[n]和
h
[
n
]
h[n]
h[n]的信号波形如图3-14所示。
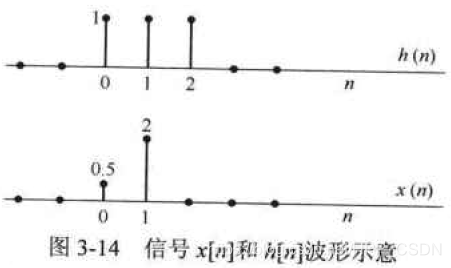
这是两个离散的时间信号。在
x
[
0
]
x[0]
x[0]和
x
[
1
]
x[1]
x[1]以外,
y
[
n
]
y[n]
y[n]都为0。
y
[
n
]
=
∑
k
=
−
∞
+
∞
x
[
k
]
h
[
n
−
k
]
=
x
[
0
]
h
[
n
−
0
]
+
x
[
1
]
h
[
n
−
1
]
=
0.5
h
[
n
−
0
]
+
2
h
[
n
−
1
]
(3-7)
y[n] = \sum_{k=-\infty}^{+\infty} x[k]h[n-k] = x[0]h[n-0] + x[1]h[n-1] = 0.5h[n-0] + 2h[n-1] \tag{3-7}
y[n]=k=−∞∑+∞x[k]h[n−k]=x[0]h[n−0]+x[1]h[n−1]=0.5h[n−0]+2h[n−1](3-7)
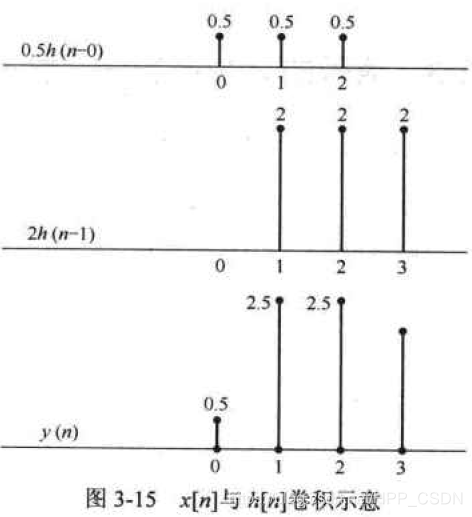
0.5
h
[
n
−
0
]
0.5h[n-0]
0.5h[n−0]相当于将
h
[
n
]
h[n]
h[n]的值全部乘以0.5,再向右移0位。
2
h
[
n
−
1
]
2h[n-1]
2h[n−1]相当于将
h
[
n
]
h[n]
h[n]的值全部乘以2,再向右移1位。最后将它们叠加一起,这就是这两个信号卷积的结果。
对于连续信号的卷积,可以假设它是离散的 (微分),然后用积分求之。
x
(
t
)
∗
h
(
t
)
=
∫
−
∞
∞
x
(
τ
)
h
(
t
−
τ
)
d
τ
(3-8)
x(t)*h(t) = \int_{-\infty}^{\infty}x(\tau)h(t-\tau)d\tau \tag{3-8}
x(t)∗h(t)=∫−∞∞x(τ)h(t−τ)dτ(3-8)
卷积计算的另外一种方法,还是以图3-14所示为例,保持
x
[
n
]
x[n]
x[n]不变,将
h
[
n
]
h[n]
h[n]先反转过来。
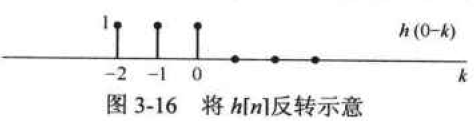
再把反转后的
h
[
n
]
h[n]
h[n]移到
x
[
n
]
x[n]
x[n]的左边。
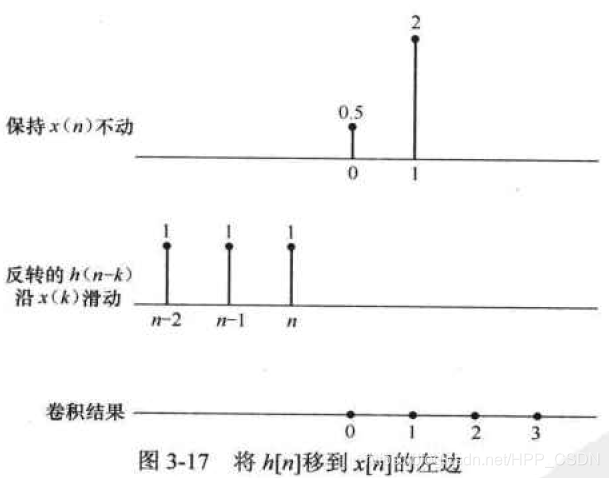
将
h
[
n
−
k
]
h[n-k]
h[n−k]沿
x
[
k
]
x[k]
x[k]向右滑动。当
h
[
n
−
k
]
h[n-k]
h[n−k]和
x
[
k
]
x[k]
x[k]的非零值没有重合时,相乘为0。当有一个重合时,重合值相乘为0.5。
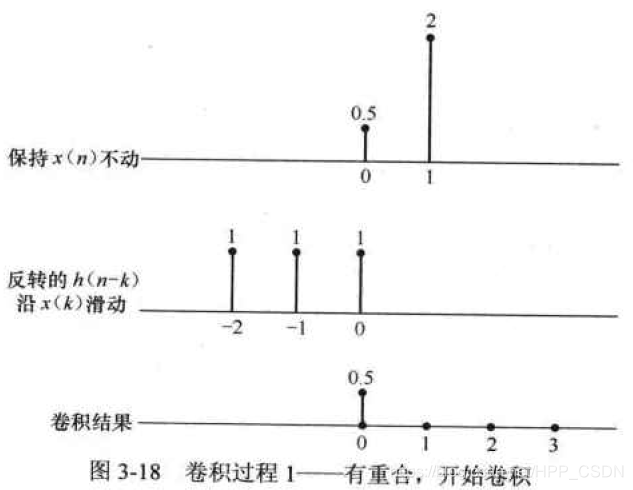
继续右滑,当有两个重合时,两个重合值分别相乘并相加得2.5。
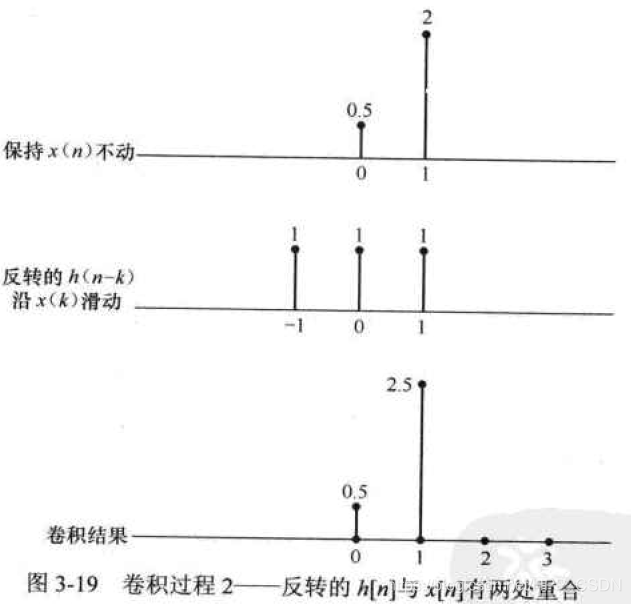
继续右移,有两个重合值,将这两个重合值分别相乘并相加得到2.5。
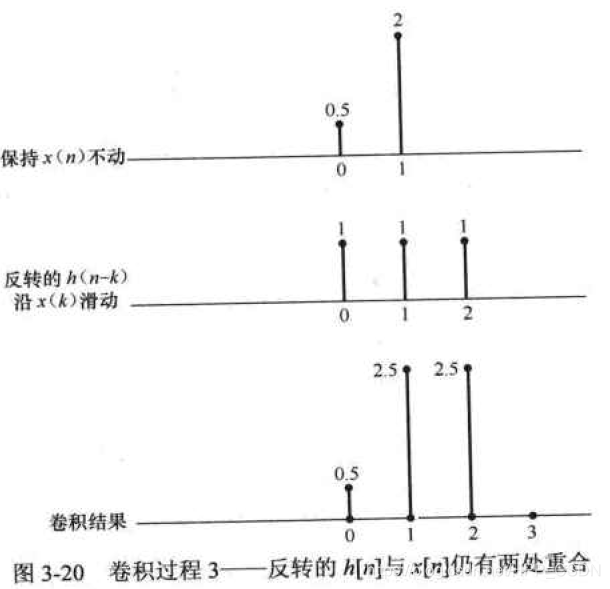
继续右移,有一个重合值,相乘得2,最后将4个值叠加,就是卷积的结果。
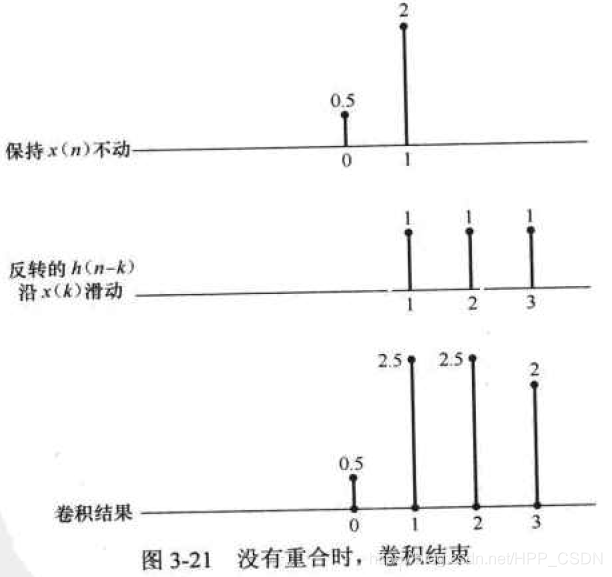
这就是说,卷积运算可以将其中一个波形反转,并移位到另一波形的左侧,首尾相接,然后开始向右滑动,将重叠部分相乘后叠加或积分,直至没有重叠。重合越多,卷积值越大。
现在把这一方法推广到连续频谱的情形。假设有两个数字信号的频谱,一个低速的,频谱窄些,一个是高速的,频谱较宽,如图3-22所示。
现在,将第一个信号的频谱反转,然后挪到另一个频谱的左边,首尾相接,然后再沿
ω
\omega
ω轴向右滑动;当有重叠时,重叠部分相乘相加后将得到一个数值 (改数值等于重叠部分的面积),重叠越多,面积越大,因而数值越大;当完全重合时,数值达到最大;接着重合开始减少,数值减少,最后没有重合,卷积结束,这就得到了两个信号卷积后的频谱。
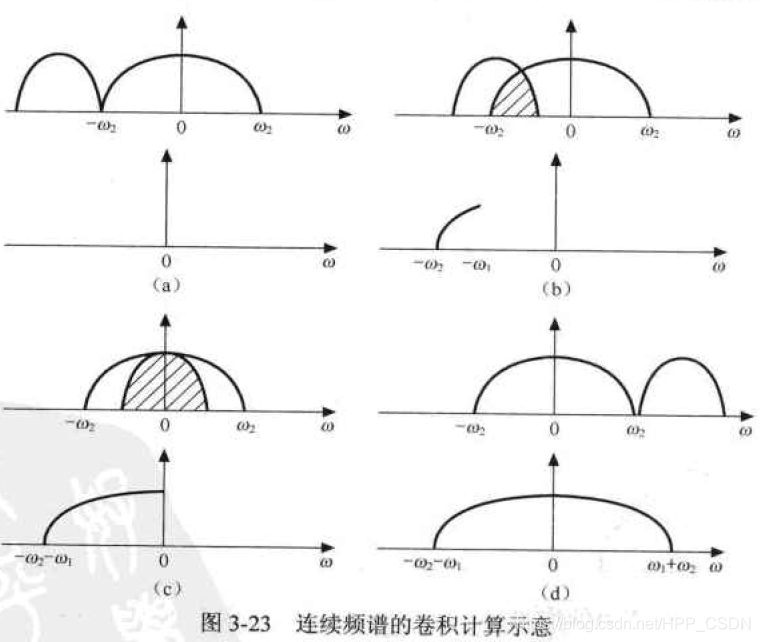
从卷积结果来看,两信号相乘后,对于第一个信号,它的频谱被扩展了。这是扩频通信的基本原理。
知乎:如何通俗易懂地解释卷积?
信号的处理
为什么要调制呢?
这是因为在通信系统中,任何特定的信道都有一个与其相关的频率范围,比如双绞线、同轴电缆、电磁波等,都只能传输一定频率范围内的信号。
而我们要传输的信号,其频率不一定就恰巧在该范围之内。
那就需要将信号频率搬到信道频率范围之内。
这个频谱搬移的过程就称为调制。
调制在电路中是通过乘法器来实现的,如图3-24所示。
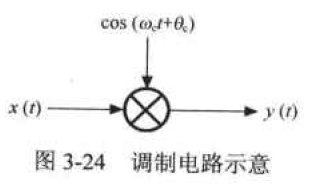
这里,
x
(
t
)
x(t)
x(t)是输入信号,
cos
(
ω
c
t
)
\cos(\omega_c t)
cos(ωct)称为载波,
y
(
t
)
y(t)
y(t)是调制后的信号,
y
(
t
)
=
x
(
t
)
cos
(
ω
c
t
)
y(t)=x(t)\cos(\omega_c t)
y(t)=x(t)cos(ωct)。
时域中相乘,在频域中就是卷积。要判断相乘后信号的频率是否在信道要求的频率范围内,在频域中把它们的频谱卷积一下就清楚了。
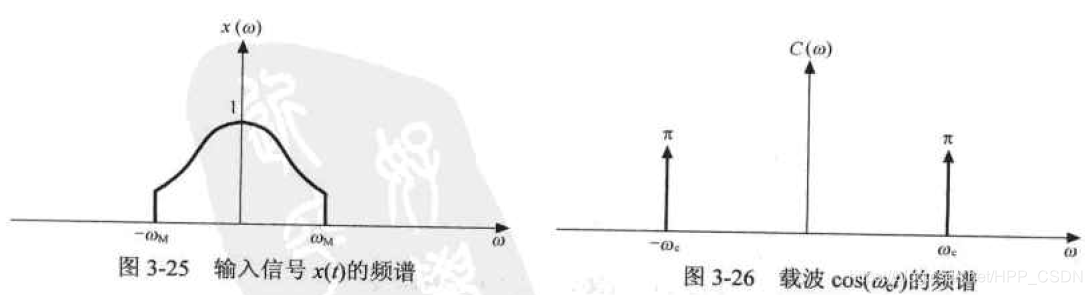
假设
x
(
t
)
x(t)
x(t)的频谱如图3-25所示,载波的频谱如图3-26所示。现在将这两个频谱卷积。卷积后的频谱如图3-27所示。
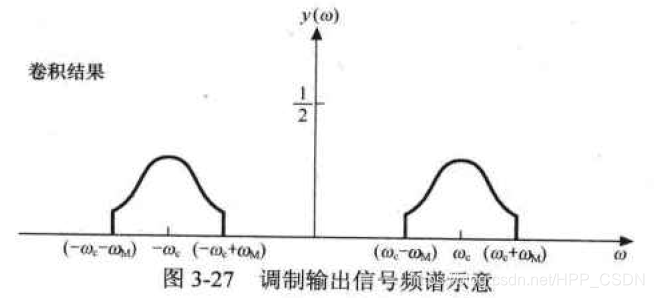
很像把输入信号的频谱搬到了载波频谱上一样,所以也把这个电路称为频谱搬移电路。
在解调时,我们仍然要用这个频谱搬移电路,把这个已调信号的频谱再往载波频谱上搬一次。
解调的电路如图3-28所示。
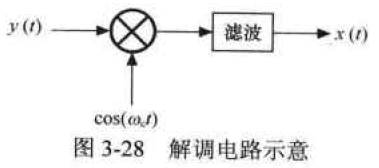
y
(
t
)
y(t)
y(t)调制的输出信号,这一次是作为解调电路的输入信号来和载波相乘的。将输入信号的频谱搬到载波频谱上,卷积后的频谱如图3-29所示。

因为有重叠,虚框这一部分的频谱得到了加强,这个得到加强的频谱和原始信号的频谱是一样的。用滤波器可以把左右两边上的频谱过滤掉,只保留这一个频谱,这样就恢复出原始信号了。
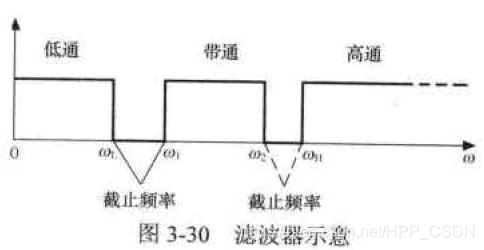
滤波器的作用是允许某一部分频率的信号顺利地通过,而抑制另外一部分频率的信号,实质上是一个选频电路。
通常把信号能够通过的频率范围称为通频带或通带;把信号受到抑制的频率范围称为阻带;通带和阻带之间的分界频率称为截止频率。
根据所通过信号的频段,滤波器可分为低通、高通、带通和带阻滤波器 4 种。
- 低通滤波器允许信号中的低频或直流分量通过,抑制高频分量;
- 高通滤波器允许信号中的高频分量通过,抑制低频或直流分量;
- 带通滤波器允许一定频段的信号通过,抑制低于或高于该频段的信号;
- 带阻滤波器抑制一定频段内的信号,允许该频段以外的信号通过。
在已调信号的频谱中,把载频两边的频谱称为上边带和下边带。
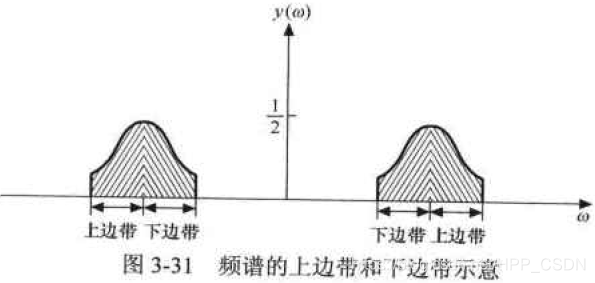
通过解调过程我们发现,其实只需要单独的上边带或下边带,就可以恢复出原始信号。这就是说,在已调信号中,存在多余的频谱,如果去掉这些多余的频谱,仅保留下边带或上边带的话,频带和发射机功率的使用都会更加经济有效。这个在实际的通信电路中被普遍采用。
怎么去掉多出的一个边带呢?看图3-32所示的一个电路。
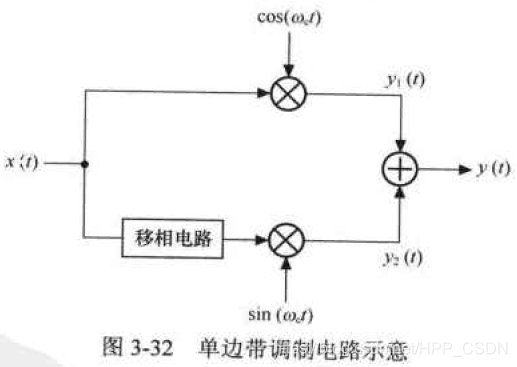
这个电路将输入信号分为两路分别进行调制,其中一路的载波为余弦函数,另一路的载波为正弦函数,调制后再将两路信号叠加,作为调制的输出信号。
其中在正弦载波调制前加了一个“90°移相网络”,其作用是将该路信号频谱的上边带翻转,这样经过调制的频谱搬移后,和余弦支路上的调制频谱就有一个边带的幅值是相反的,这样信号叠加后,这一个边带就被抵消了,只保留了另一个边带。
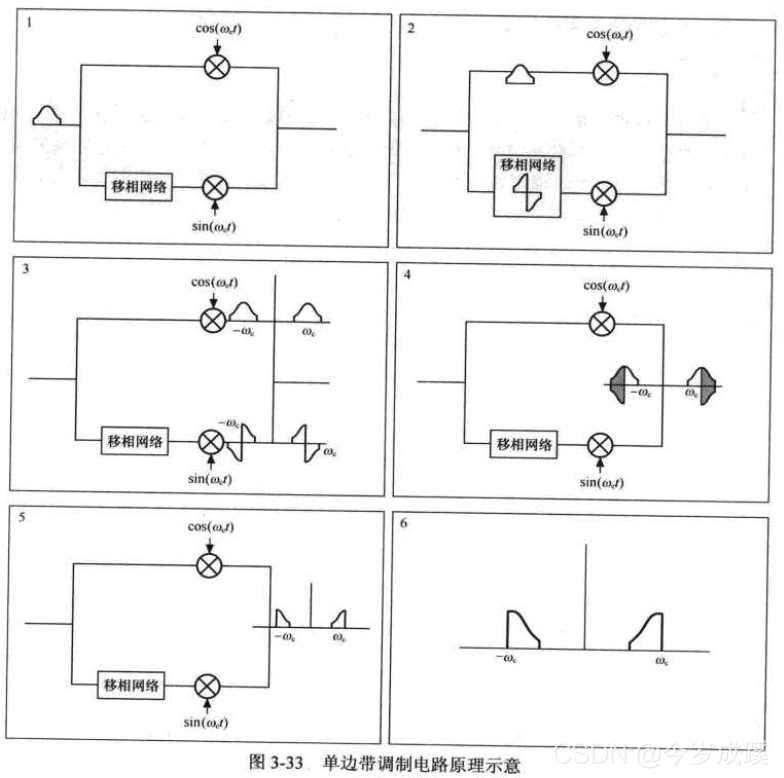
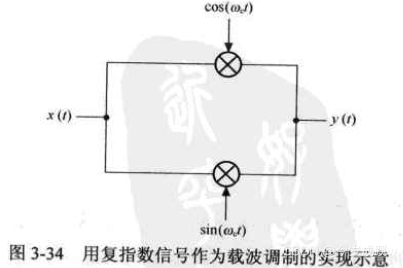
复指数函数与正弦函数密切相关,根据欧拉公式,复指数信号可以用正弦信号来表示:
e
j
ω
t
=
cos
ω
t
+
j
sin
ω
t
e^{j\omega t} = \cos \omega t + j\sin \omega t
ejωt=cosωt+jsinωt。这个单边带调制电路的两个支路,如果忽略移相电路,就正好可以代表复指数信号的实部和虚部,所以图3-34所示的电路也是复指数信号调制的实现方式。
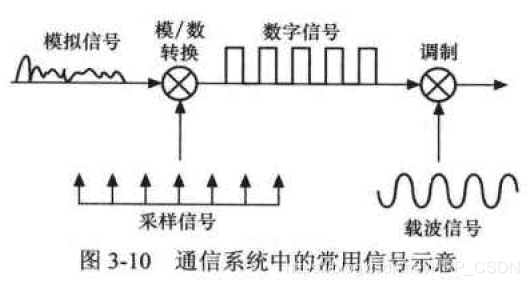
采样是将模拟信号转换为数字信号的基础。由于数字信号是离散时间信号,所以要将模拟信号转换为数字信号,首先需要通过采样,将连续时间信号用等时间间隔点上的样本来表示,而通过这些样本还能还原回原来的连续信号。
采用电路的实现是通过乘法器,将输入信号和采样信号进行相乘。
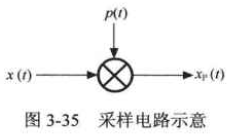
假设
x
(
t
)
x(t)
x(t)是普通的信号,
p
(
t
)
p(t)
p(t)是周期的冲激串,是理想的采样信号。
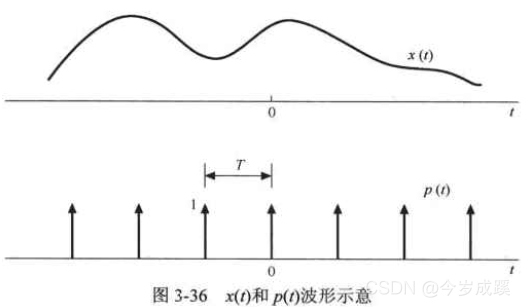
这两个信号相乘时,只在冲激发生的这些点上才有输出值,因为冲激强度为 1,这就相当于在冲激发生点上把信号
x
(
t
)
x(t)
x(t)的样本值采出来了。
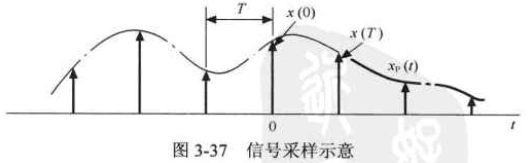
利用这样的一串样本值能不能恢复出被采样的信号呢?
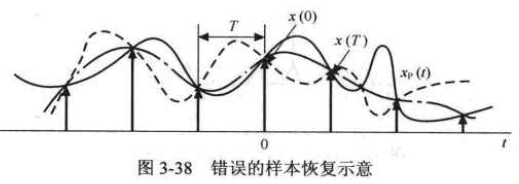
为什么会恢复出错误的波形呢?是采样间隔太大了,应该变得密一点,也就是采样频率要高一点。那要多大才合适呢?到频域中找结论。
假设输入信号的频谱和采样信号的频谱如图3-39所示。
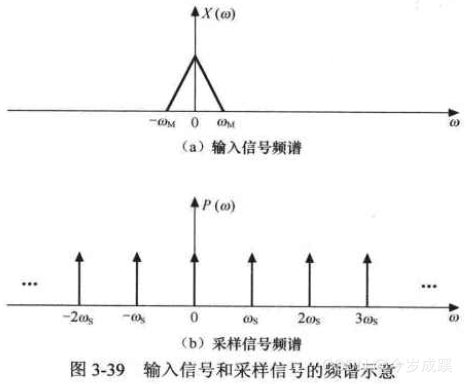
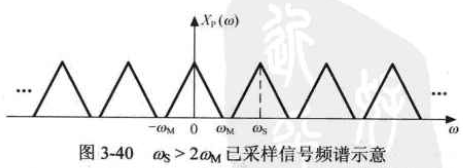
时域中两个信号相乘,频域中是要卷积的。借助调制的卷积经验,直接将输入信号的频谱搬到采样信号的频谱上,就得到卷积后的频谱,即输出信号的频谱。
如果采样频率过小,已采样信号的频谱就会有重叠。
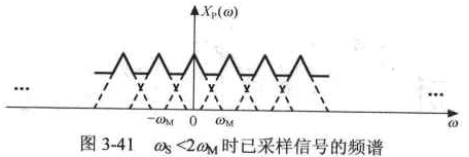
如果要完全恢复出被采样的信号,那么已采样信号的频谱里应存在完整的被采样信号的频谱。
采样频率必须要大于被采样信号的最高频率的两倍。这也是低通信号的采样定理。
信号的能量和功率
主要谈论的电通信。电通信的信号和电有关,电有能量、功率、电压、电流、电阻等。
信号功率通常定义为电流在单位电阻上消耗的功率,单位为瓦 (W)。
P
=
V
2
/
R
=
I
2
R
(W)
(3-9)
P = V^2/R = I^2R \ \text{(W)} \tag{3-9}
P=V2/R=I2R (W)(3-9)
当电阻的阻值为 1
Ω
\Omega
Ω时,这个信号功率也叫归一化功率,归到1
Ω
\Omega
Ω上消耗的功率的意思。归一化功率见式3-10。
P
=
V
2
=
I
2
(W)
(3-10)
P = V^2 = I^2 \text{(W)} \tag{3-10}
P=V2=I2(W)(3-10)
因为电信号的电压或电流是时间函数,幅值随时间而变化,假设用
f
(
t
)
f(t)
f(t)来表示,那么信号的瞬时功率为
f
2
(
t
)
f^2(t)
f2(t)。于是,信号的能量即为瞬时功率在时间上的积分,见式3-11。
E
=
∫
−
∞
∞
f
2
(
t
)
d
t
(3-11)
E = \int_{-\infty}^{\infty} f^2(t) dt \tag{3-11}
E=∫−∞∞f2(t)dt(3-11)
如果这个积分值存在的话,说明信号的能量是有限的,通常把能量有限的信号称为能量信号。一般情况下,持续时间有限的波形,其能量是有限的,所以都是能量信号。
而持续时间无限的波形,其积分值显然会无穷大,实际上没有意义。这时如果将积分值除以同样趋于无穷大的时间
T
T
T,再求极限,则可能求得一个有限的值,通常就把这个值称为信号的平均功率。
S
=
lim
T
→
∞
1
T
∫
−
T
/
2
T
/
2
f
2
(
t
)
d
t
(3-12)
S = \lim_{T\rightarrow\infty} \frac{1}{T}\int_{-T/2}^{T/2} f^2(t) dt \tag{3-12}
S=T→∞limT1∫−T/2T/2f2(t)dt(3-12)
这种能量无限但平均功率有限的信号称为功率信号。通常周期信号都是功率信号。
能量谱密度是指能量信号的能量在频域中的分布。
功率谱密度是功率信号的功率在频域中的分布。
能量谱密度和功率谱密度可以通过巴塞法尔 (Parseval) 定理给出。能量谱密度计算见式3-13。
G
E
(
ω
)
=
∣
F
(
ω
)
∣
2
(3-13)
G_E(\omega) = | F(\omega) |^2 \tag{3-13}
GE(ω)=∣F(ω)∣2(3-13)
G E ( ω ) G_E(\omega) GE(ω)表示能量谱密度, F ( ω ) F(\omega) F(ω)是信号的傅里叶变换,即频谱函数。
功率信号的功率谱密度
P
S
(
ω
)
P_S(\omega)
PS(ω)计算见式3-14。
P
S
(
ω
)
=
∑
n
=
−
∞
∞
∣
C
n
∣
2
(3-14)
P_S(\omega) = \sum_{n=-\infty}^{\infty} |C_n|^2 \tag{3-14}
PS(ω)=n=−∞∑∞∣Cn∣2(3-14)
C n C_n Cn是功率信号的傅里叶级数的复系数,也就是信号的频谱。因为周期信号总是功率信号,而周期信号的频谱是离散的,所以它的功率谱密度也是离散的。
信号的相关特性
信号的自相关函数和信号的能量谱密度或功率谱密度是互为傅里叶变换关系的。
能量信号的自相关函数的定义,见式3-15。
R
(
τ
)
=
∫
−
∞
∞
f
(
t
)
f
(
t
+
τ
)
d
t
(
−
∞
<
τ
<
∞
)
(3-15)
R(\tau) = \int_{-\infty}^{\infty} f(t)f(t+\tau)dt \quad (-\infty < \tau < \infty) \tag{3-15}
R(τ)=∫−∞∞f(t)f(t+τ)dt(−∞<τ<∞)(3-15)
功率信号的自相关函数的定义,见式3-16。
R
(
τ
)
=
lim
T
→
∞
1
T
∫
−
T
/
2
T
/
2
f
(
t
)
f
(
t
+
τ
)
d
t
(
−
∞
<
τ
<
∞
)
(3-16)
R(\tau) = \lim_{T\rightarrow\infty} \frac{1}{T} \int_{-T/2}^{T/2} f(t)f(t+\tau)dt \quad (-\infty < \tau < \infty) \tag{3-16}
R(τ)=T→∞limT1∫−T/2T/2f(t)f(t+τ)dt(−∞<τ<∞)(3-16)
前面说过的卷积运算的等式如式3-17所示。
f
1
(
t
)
∗
f
2
(
t
)
=
∫
−
∞
∞
f
1
(
τ
)
f
2
(
t
−
τ
)
d
τ
(3-17)
f_1(t)*f_2(t) = \int_{-\infty}^{\infty} f_1(\tau)f_2(t-\tau)d\tau \tag{3-17}
f1(t)∗f2(t)=∫−∞∞f1(τ)f2(t−τ)dτ(3-17)
将自相关函数中的积分变量变换一下。先令
τ
=
t
,
t
=
x
\tau = t, t=x
τ=t,t=x,代入式3-15得式3-18。
R
(
t
)
=
∫
−
∞
∞
f
(
x
)
f
(
x
+
t
)
d
x
(3-18)
R(t) = \int_{-\infty}^{\infty}f(x)f(x+t)dx \tag{3-18}
R(t)=∫−∞∞f(x)f(x+t)dx(3-18)
再令
x
=
−
τ
x=-\tau
x=−τ,则
R
(
t
)
R(t)
R(t)可用式3-19表示。
R
(
t
)
=
∫
−
∞
∞
f
(
−
τ
)
f
(
t
−
τ
)
d
τ
=
f
(
−
t
)
∗
f
(
t
)
(3-19)
R(t) = \int_{-\infty}^{\infty} f(-\tau)f(t-\tau)d\tau = f(-t)*f(t) \tag{3-19}
R(t)=∫−∞∞f(−τ)f(t−τ)dτ=f(−t)∗f(t)(3-19)
这和卷积运算很接近了,特别是当 f ( t ) f(t) f(t)为偶函数时,就和卷积运算完全一样了。这就是说,自相关函数是可以通过卷积运算来计算的。
在卷积运算时,“滑动”过程中两个信号重合越多,卷积越大。这说明,所谓的相关,可以理解为信号之间的重合或相似的程度。相关值越大,重合程度就越大。重合点越多,相似程度越高。
自相关函数反映了一个信号与其延迟了 τ \tau τ秒后的信号间相关的程度。这个相关的程度,只和时间差 τ \tau τ有关。
互相关描述两个信号间相互关联的程度。定义和自相关相似,将延迟的信号换为另一个信号的延迟,见式3-20。
R
12
(
τ
)
=
∫
∞
∞
f
1
(
t
)
f
2
(
t
+
τ
)
d
t
(
−
∞
<
τ
<
∞
)
(3-20)
R_{12}(\tau) = \int_{\infty}^{\infty}f_1(t)f_2(t+\tau)dt \quad (-\infty < \tau < \infty) \tag{3-20}
R12(τ)=∫∞∞f1(t)f2(t+τ)dt(−∞<τ<∞)(3-20)
互相关函数反映了一个信号与延迟了 τ \tau τ秒后的另一个信号间相关的程度。只和时间差 τ \tau τ有关。
自相关函数和功率谱密度在理解随机信号时会比较有用。
频域特性也就是频率特性,主要包括信号的频谱、能量谱密度和功率谱密度,很重要的,与信号的占用频带宽度、信号的抗噪声能力等有密切的关系。
时域特性就是自相关函数和互相关函数。
习题
-
正弦信号 f ( t ) = 3 cos ( 12 π t + 30 ) f(t) = 3\cos(12\pi t+30) f(t)=3cos(12πt+30)的幅度是多少V,频率是多少Hz,相位是多少弧度?
解:最大幅度 A = 3 A = 3 A=3。
频率 f = ω 0 / ( 2 π ) = 6 f = \omega_0 / (2\pi) = 6 f=ω0/(2π)=6。
信号的相位是 ( 12 π t + 30 ) (12\pi t+30) (12πt+30),初始相位是 30 弧度。 -
假设有信号 f ( t ) f(t) f(t)的傅里叶级数为: f ( t ) = 1 + 1 / 2 e j 2 t + 1 / 2 e − j 2 t + 1 / 4 e j 4 t + 1 / 4 e − j 4 t f(t) = 1 + 1/2e^{j2t} + 1/2e^{-j2t} + 1/4e^{j4t} + 1/4e^{-j4t} f(t)=1+1/2ej2t+1/2e−j2t+1/4ej4t+1/4e−j4t,试指出该信号的基波频率,并画出该信号的频谱图。
解:基波 ω 0 = 2 \omega_0 = 2 ω0=2。
频谱图如图2所示。
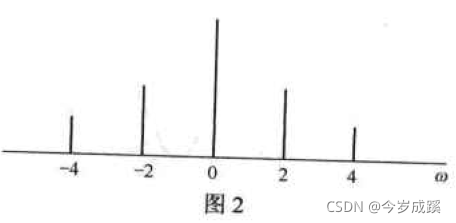
-
已知 f ( t ) f(t) f(t)为非周期信号,请说明求 f ( t ) f(t) f(t)频谱的思路。
解:周期信号的周期无限扩大就是非周期信号了。频率和周期是反比的关系,周期无限扩大,频率间隔就要无限地缩小,逼近连续了。
可以使用傅里叶变换 (式3-5) 从信号的时间函数 f ( t ) f(t) f(t)求信号的频谱 F ( ω ) F(\omega) F(ω)。 -
已知信号 x [ n ] x[n] x[n]和 h [ n ] h[n] h[n]的频谱如图3-42所示,请求出 x [ n ] ∗ h [ n ] x[n]*h[n] x[n]∗h[n]的频谱。
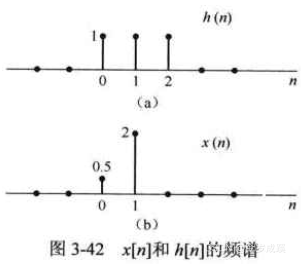
解: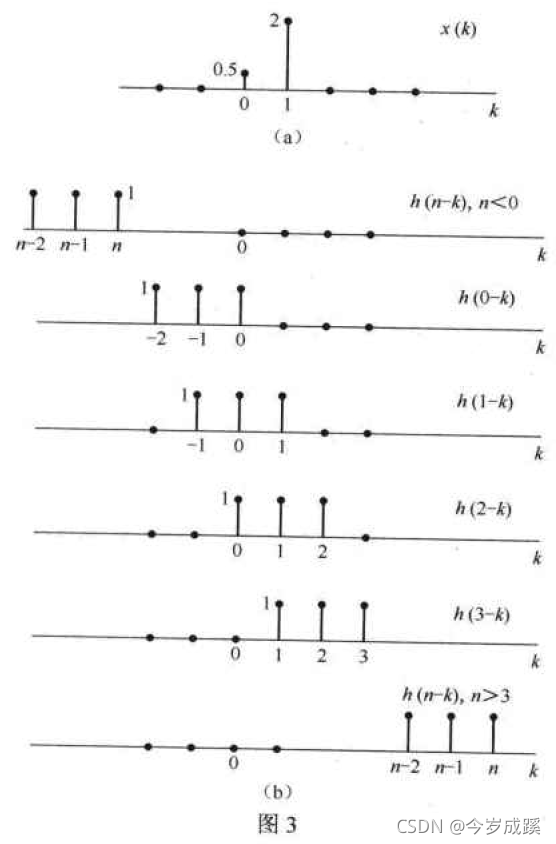
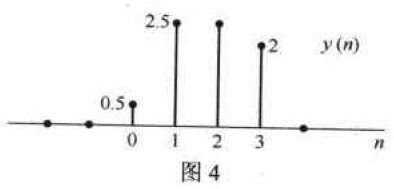
-
请写出与图3-43所示的频谱对应的信号的时间函数,并画出相应的波形。
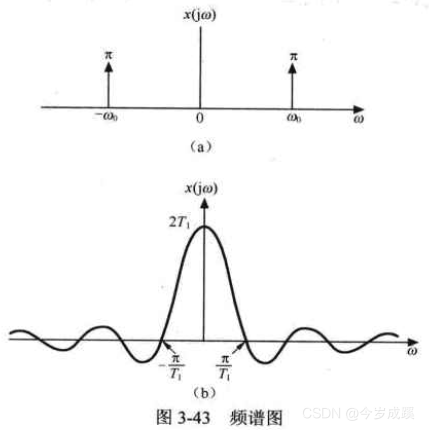
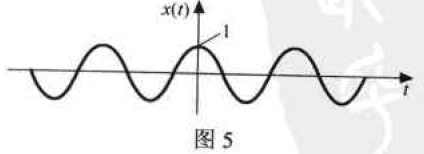
解:通过傅里叶反变换 (式3-3) 从信号的频谱求解信号的时间函数。
(a) x ( t ) = cos ω 0 t x(t) = \cos \omega_0t x(t)=cosω0t,如图5所示。
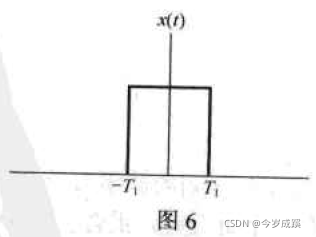
(b) x ( t ) = { 1 , ∣ t ∣ < T 1 0 , ∣ t ∣ > T 1 x(t) = \begin{cases}1, \ |t|<T_1 \\0, \ |t|>T_1 \end{cases} x(t)={1, ∣t∣<T10, ∣t∣>T1,如图6所示。
-
请解释能量谱密度和功率谱密度,并简述它们与自相关函数的关系。
解:能量谱密度是指能量信号的能量在频域中的分布,功率谱密度是指功率信号的功率在频域中的分布。
信号的自相关函数和信号的能量谱密度或功率谱密度是互为傅里叶变换的关系,也就是说,通过信号的自相关函数,可以求得信号的能量谱密度或功率谱密度,而通过能量谱密度或功率谱密度,也可以求得信号的自相关函数。






















 532
532











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








