目录
定义在【0，π】的函数展开为正弦或余弦级数，进行延拓，断点和端点在【-π，π】上讨论
第一节 常数项级数的概念和性质
常数项级数：无穷个数的和
那么一定发散
题目练习
类型一 判断级数的收敛性（含调和级数）
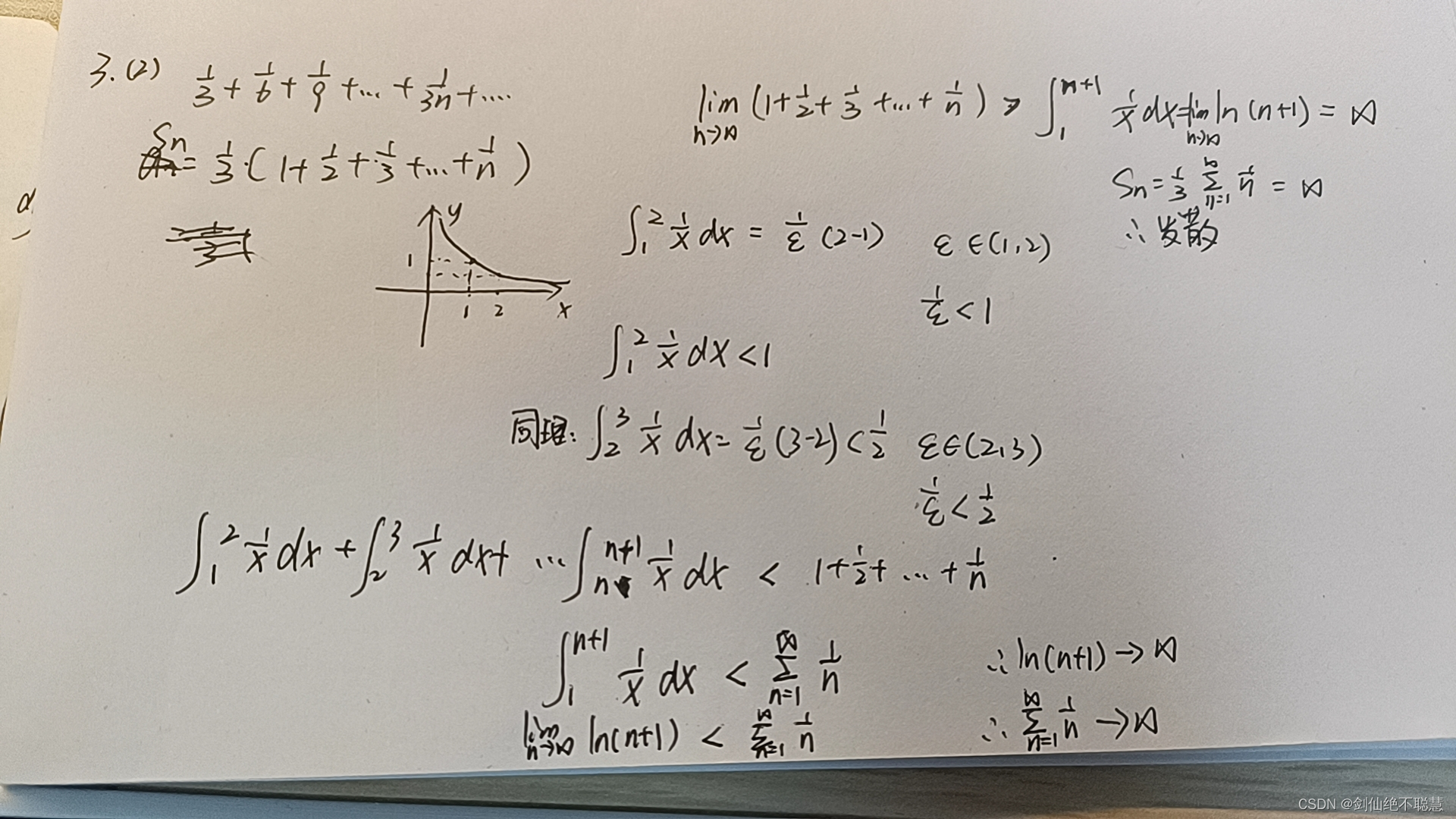
第二节 常数项级数的审敛法
正项级数及其审敛法
比较法和比较法的极限形式一般和p级数，等比数列相比较
当遇到三大巨头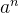
、
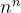、n!首先用比值法和根值法
交错级数及其审敛法
绝对收敛和条件收敛
题目练习
类型一 比较法和比较法的极限形式
类型二 比值法和根值法
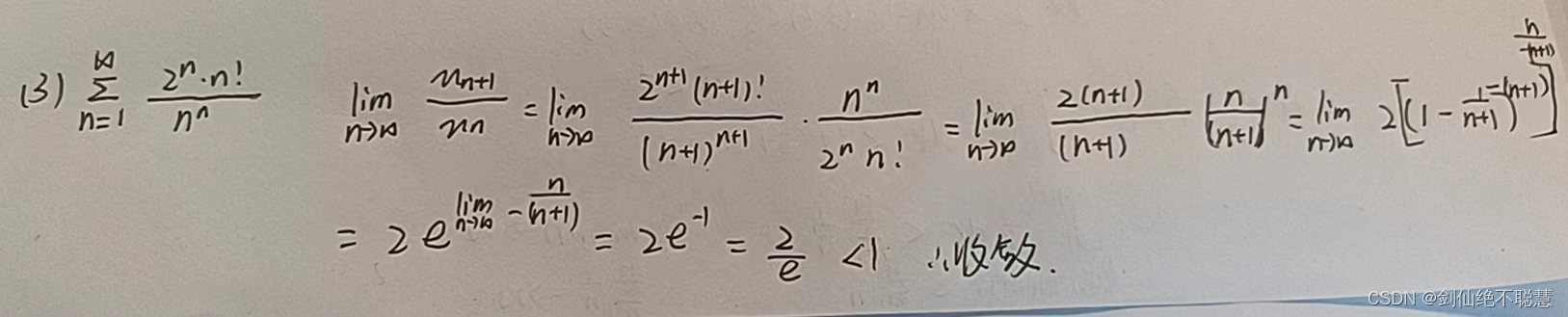
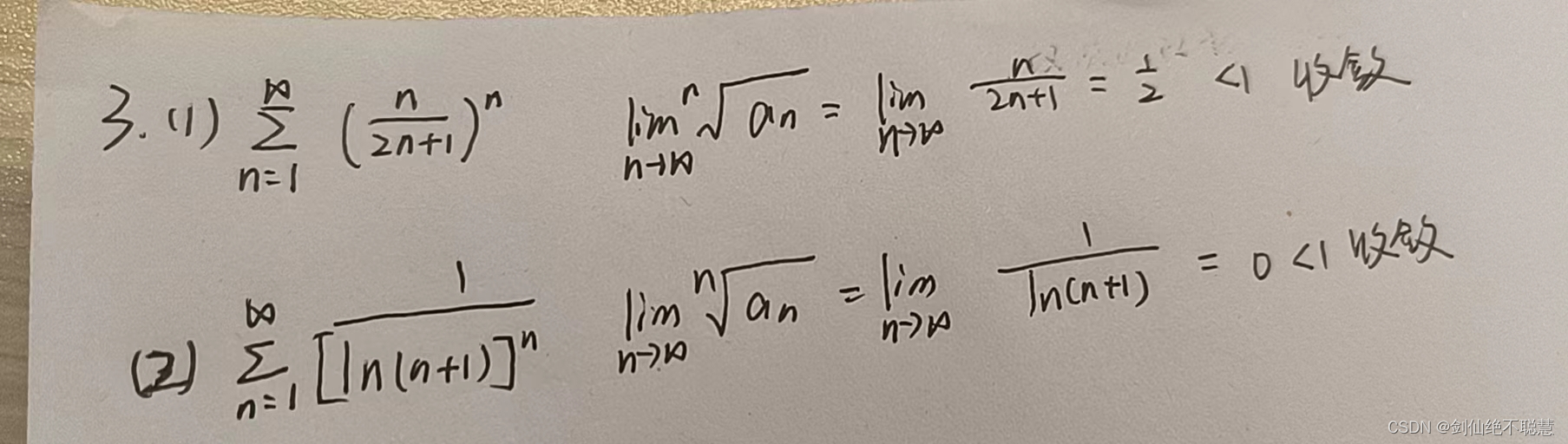
类型三 交错级数是绝对收敛还是条件收敛
第三节 幂级数
幂级数及其收敛性
阿贝尔定理
注意此处为,如果为
或者为
则需要另行讨论（题目练习中会涉及）
收敛半径，收敛区间，收敛域的区别
收敛半径为R
收敛区间为开区间（-R,R）
收敛域需要对边界x=+-R进行讨论
幂级数的性质
题目练习
类型一 求幂级数的收敛区间
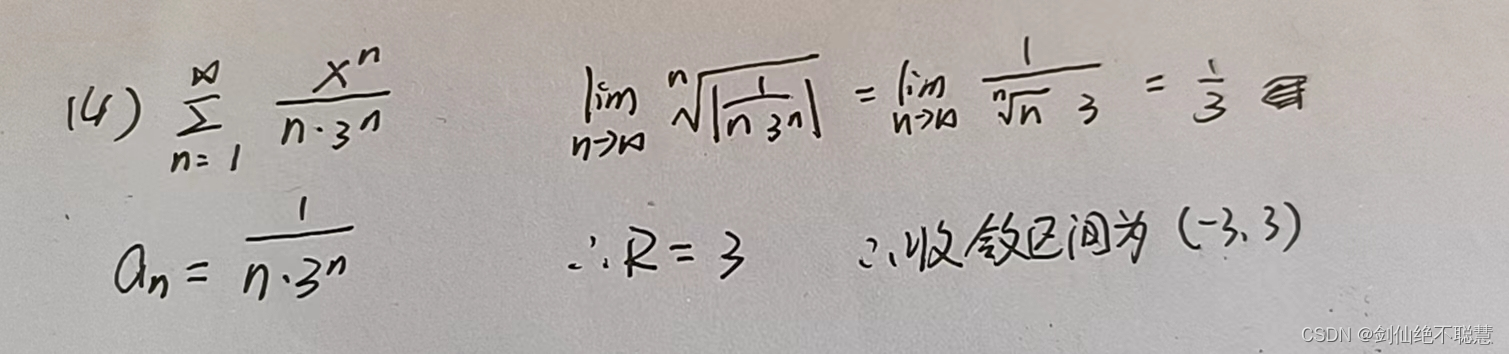
类型二 求含缺项的幂级数的收敛区间
收敛区间是收敛点的集合，则当ρ<1则收敛，找到最大的点，即可确定收敛区域
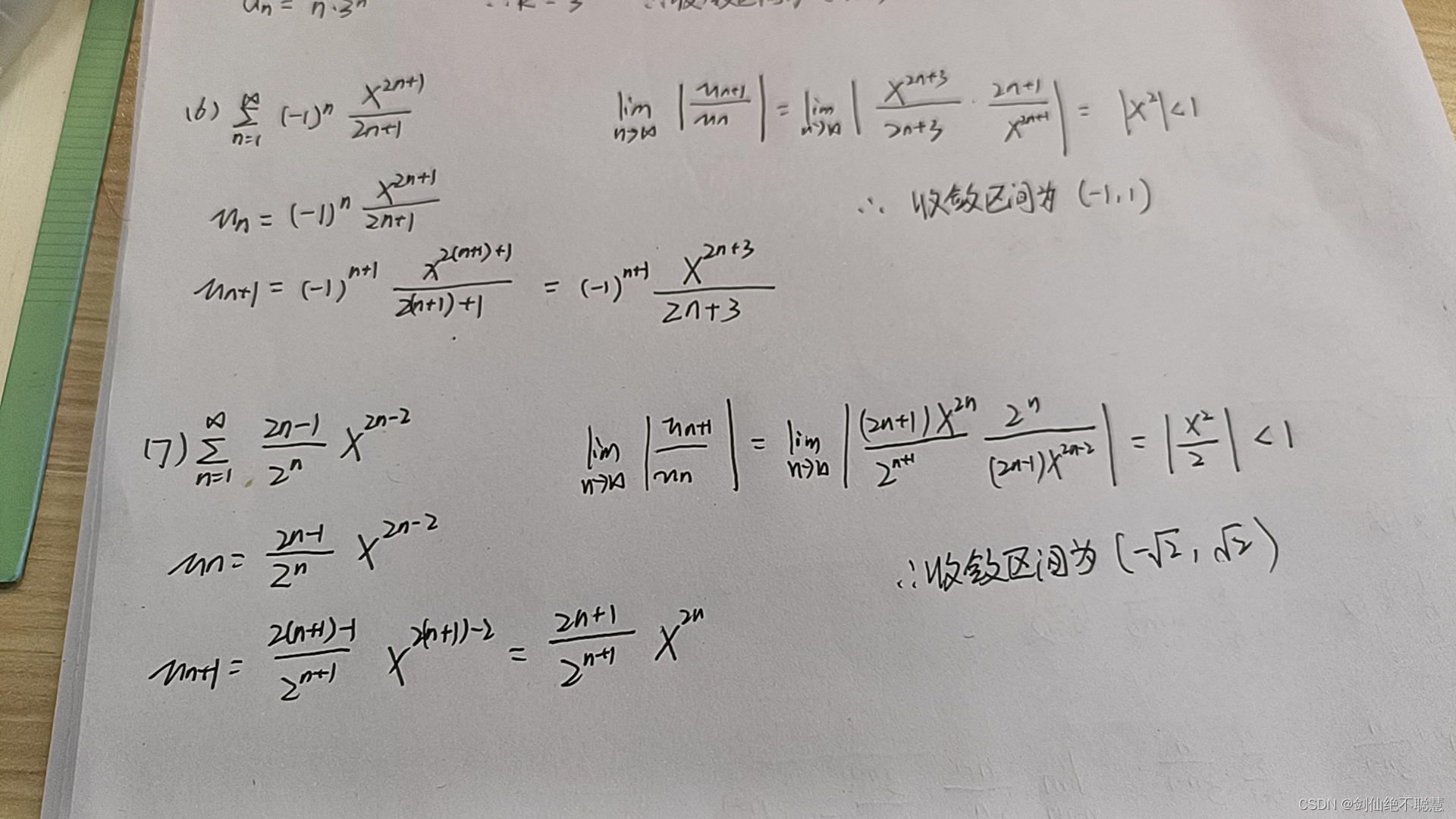
类型三 求幂级数收敛域
类型四 利用逐项求导或逐项积分求和函数
关键公式
以及
第四节 函数展开成幂级数
题目练习
类型一 将函数展开成x的幂级数
分式
积分
类型二 将函数展开成（x+n）的幂级数
三角函数
非三角函数
第五节傅里叶级数
函数展开成傅里叶级数
对间断点和端点需要讨论
f(x)为奇函数或者偶函数
定义在【0，π】的函数展开为正弦或余弦级数，进行延拓，断点和端点在【-π，π】上讨论
题目练习
类型一 对周期为2π的函数展开为傅里叶级数
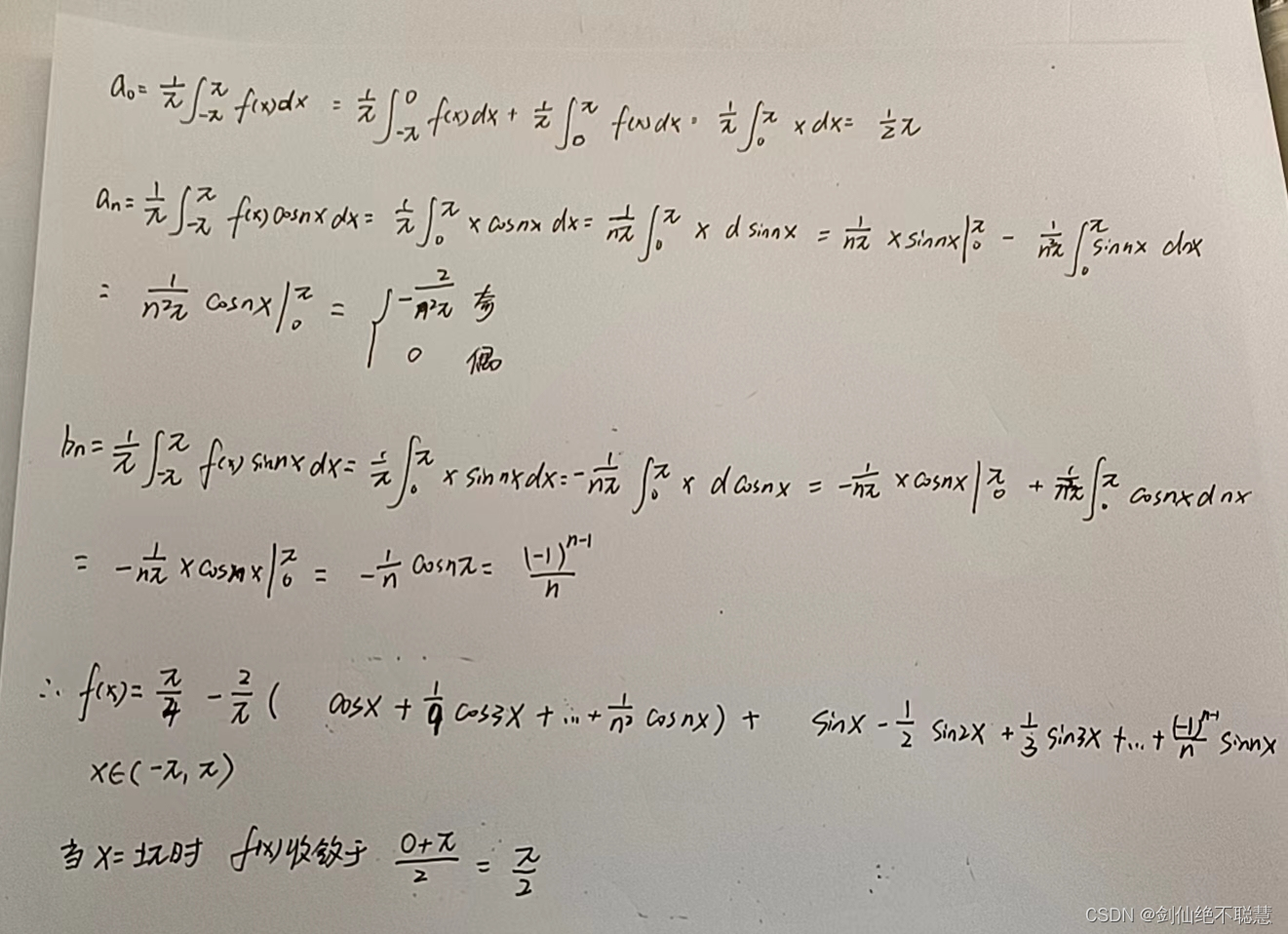
类型二 对f(x)为奇函数或者偶函数展开为傅里叶级数
类型三 对定义在【0，π】的函数展开为正弦级数和余弦级数
第六节 一般周期函数的傅里叶级数
周期为2l的函数展开为傅里叶级数
在任意有限区间上函数的傅里叶级数展开
题目练习
类型一 周期为2l
类型二 在l上展开为周期为2l的余弦或正弦级数
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
