分类:概率生成模型
Classification: Probabilistic Generative Model
回归做分类?NO!
——用Regreesion强制做Classification
——NO!!!!
以二分类举例的情况下,如果回归的数值越接近于1,则我们认为是正类;否则为负类。
在这样的训练集上进行回归,某种程度上是能够拟合出一个较好的分界,使得上述成立。
但是,也有可能是,属于某个正类的回归预测值非常非常大,这样的情况下,它会error地得到另一个分界
因为回归定义分界的好坏是(Loss Function),是点到线的距离差的平方和(某种Loss Function)
而这种定义对分类来说,是不适用的

而且,这种情况下,相当于默认了某种Class的关系
比如,在多分类问题里:
——我们将Class 1 means the target is 1; Class 2 means the target 2;Class 3 means the target 3;…
在这种情况下,我们有可能会认为第二类与第三类比较近,第四类和第三类比较远,但实际上,我们的类上并不存在这样的关系。
做法
-
Function(Model)
输入x后,若f(x)>0 则输出类型1;否则输出类型2
-
Loss Function
L ( f ) = ∑ n δ ( f ( x n ) ≠ y ^ n ) L(f)=\sum_n\delta(f(x^n)\neq \hat{y}^n) L(f)=n∑δ(f(xn)=y^n)
我们希望它预测错误的次数越少越好 -
Find the best function:
- Example:Perceptron,SVM

生成模型
利用条件概率——贝叶斯公式进行分类
假设给我一个x,那么这个x属于Class 1的几率就为
P
(
C
1
∣
x
)
=
P
(
C
1
∗
x
)
P
(
x
)
=
P
(
x
∣
C
1
)
P
(
C
1
)
P
(
x
∣
C
1
)
P
(
C
1
)
+
P
(
x
∣
C
2
)
P
(
C
2
)
P(C_1|x)=\frac{P(C_1*x)}{P(x)}=\frac{P(x|C_1)P(C_1)}{P(x|C_1)P(C_1)+P(x|C_2)P(C_2)}
P(C1∣x)=P(x)P(C1∗x)=P(x∣C1)P(C1)+P(x∣C2)P(C2)P(x∣C1)P(C1)
属于哪个类的概率越大,则x属于这个类
——如何得到 P ( x ∣ C 1 ) P(x|C_1) P(x∣C1)
高斯分布
假设说,我们没有见过这个x,那么在训练集上,这个 P ( x ∣ C 1 ) P(x|C_1) P(x∣C1)的概率就是显而易见为0——这是不正确的!
因为这个x其实是——特征向量(A feature vector)
我们可以理解为——我们的训练集是,从一个Gaussian的分布里(也可能是别的分布),采样出来的点,我们通过研究采样的点,来找到Gaussian的分布
——高斯分布(即正态分布)——也可能是别的密度分布函数
——本质上,我们输入一个vector(特征向量),那么在分布里,我们就能找到,采样到这个向量的可能性(即分布中常提到的密度分布)
- 输入:vector x
- 输出:Sampling x的可能性
这个分布函数的形状,取决于mean μ \mu μ 和 covariance matrix Σ \Sigma Σ
——即取决于均数和协方差矩阵
——注意,这里的均数 μ \mu μ也是一个vector
f μ , Σ ( x ) = 1 ( 2 π ) D / 2 1 ∣ Σ ∣ 1 / 2 e x p ( − 1 2 ( x − μ ) T Σ − 1 ( x − μ ) ) f_{\mu,\Sigma}(x)=\frac{1}{(2\pi)^{D/2}}\frac{1}{|\Sigma|^{1/2}}exp(-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu)) fμ,Σ(x)=(2π)D/21∣Σ∣1/21exp(−21(x−μ)TΣ−1(x−μ))

如何找到 μ \mu μ 和 Σ \Sigma Σ
Maximum Likelihood
比如你有79个点,那么就这个分布采样出这79个点的概率是最大的
——Likelihood Function
L ( μ , Σ ) = f μ , Σ ( x 1 ) f ( x 2 ) . . . f ( x 79 ) L(\mu,\Sigma)=f_{\mu,\Sigma}(x_1)f(x_2)...f(x_{79}) L(μ,Σ)=fμ,Σ(x1)f(x2)...f(x79)
我们希望找到
μ
∗
,
Σ
∗
\mu^{*},\Sigma^*
μ∗,Σ∗, 使得
a
r
g
max
μ
,
Σ
L
(
μ
,
Σ
)
arg\max_{\mu,\Sigma}L(\mu,\Sigma)
argmaxμ,ΣL(μ,Σ)
μ
∗
=
1
79
∑
n
=
1
79
x
n
Σ
∗
=
1
79
∑
n
=
1
79
(
x
n
−
μ
∗
)
(
x
n
−
μ
∗
)
T
\mu^*=\frac{1}{79}\sum_{n=1}^{79}x^n\\ \Sigma^*=\frac{1}{79}\sum_{n=1}^{79}(x^n-\mu^*)(x^n-\mu^*)^T
μ∗=791n=1∑79xnΣ∗=791n=1∑79(xn−μ∗)(xn−μ∗)T

Why Called 生成模型
我们可以计算出每个x出现的概率,我们就知道每一个x的分布,我们就可以用这个分布来产生x,采样x
P
(
x
)
=
P
(
x
∣
C
1
)
P
(
C
1
)
+
P
(
x
∣
C
2
)
P
(
C
2
)
P(x)=P(x|C_1)P(C_1)+P(x|C_2)P(C_2)
P(x)=P(x∣C1)P(C1)+P(x∣C2)P(C2)
——全概率公式
修改模型
不同的类其实可以共用一个协方差矩阵
——因为协方差矩阵和特征size的平方成正比
因此协方差矩阵的增长非常快,如果不同的类给予不同的协方差矩阵
那么Model的参数过多,参数太多则Variance就大,那么就容易overfitting
How to Calculate
Find
μ
1
,
μ
2
,
Σ
\mu^1,\mu^2,\Sigma
μ1,μ2,Σ maximizing the likelihood
L
(
μ
1
,
μ
2
,
Σ
)
L(\mu^1,\mu^2,\Sigma)
L(μ1,μ2,Σ)
L
(
μ
1
,
μ
2
,
Σ
)
=
f
μ
1
,
Σ
(
x
1
)
f
μ
1
,
Σ
(
x
2
)
.
.
.
f
μ
1
,
Σ
(
x
79
)
∗
f
μ
2
,
Σ
(
x
80
)
.
.
.
f
μ
2
,
Σ
(
x
140
)
L(\mu^1,\mu^2,\Sigma)=f_{\mu^1,\Sigma}(x^1)f_{\mu^1,\Sigma}(x^2)...f_{\mu^1,\Sigma}(x^{79})*f_{\mu^2,\Sigma}(x^{80})...f_{\mu^2,\Sigma}(x^{140})
L(μ1,μ2,Σ)=fμ1,Σ(x1)fμ1,Σ(x2)...fμ1,Σ(x79)∗fμ2,Σ(x80)...fμ2,Σ(x140)
μ 1 , μ 2 = 1 79 ∑ n = 1 79 x n \mu^1,\mu^2=\frac{1}{79}\sum_{n=1}^{79}x^n\\ μ1,μ2=791n=1∑79xn
Σ = 79 140 Σ 1 + 61 140 Σ 2 \Sigma=\frac{79}{140}\Sigma^1+\frac{61}{140}\Sigma^2 Σ=14079Σ1+14061Σ2

——选用所有特征之后的结果

朴素贝叶斯做法

不同模型的选择
——你永远可以选择你喜欢的
你选择参数少的——Bias大,Variance小
你选择参数多的——Bias小,Variance大
——对于二值特征,你不会假设它为高斯分布,因为没有办法使得它合理
而是假设其为伯努利分布
——假设所有的特征都是独立同分布的很切合实际
那么朴素贝叶斯就会表现得非常好
后验概率
P ( C 1 ∣ x ) = P ( C 1 ∗ x ) P ( x ) = P ( x ∣ C 1 ) P ( C 1 ) P ( x ∣ C 1 ) P ( C 1 ) + P ( x ∣ C 2 ) P ( C 2 ) = 1 1 + P ( x ∣ C 2 ) P ( C 2 ) P ( x ∣ C 1 ) P ( C 1 ) = 1 1 + e x p ( − z ) = σ ( z ) P(C_1|x)=\frac{P(C_1*x)}{P(x)}=\frac{P(x|C_1)P(C_1)}{P(x|C_1)P(C_1)+P(x|C_2)P(C_2)}\\ =\frac{1}{1+\frac{P(x|C_2)P(C_2)}{P(x|C_1)P(C_1)}}=\frac{1}{1+exp(-z)}=\sigma(z) P(C1∣x)=P(x)P(C1∗x)=P(x∣C1)P(C1)+P(x∣C2)P(C2)P(x∣C1)P(C1)=1+P(x∣C1)P(C1)P(x∣C2)P(C2)1=1+exp(−z)1=σ(z)
其中 z = l n P ( x ∣ C 1 ) P ( C 1 ) P ( x ∣ C 2 ) P ( C 2 ) 其中z=ln\frac{P(x|C_1)P(C_1)}{P(x|C_2)P(C_2)} 其中z=lnP(x∣C2)P(C2)P(x∣C1)P(C1)
1 1 + e x p ( − z ) 称之为 S i g m o i d f u n c t i o n \frac{1}{1+exp(-z)}称之为Sigmoid\,\,\,function 1+exp(−z)1称之为Sigmoidfunction
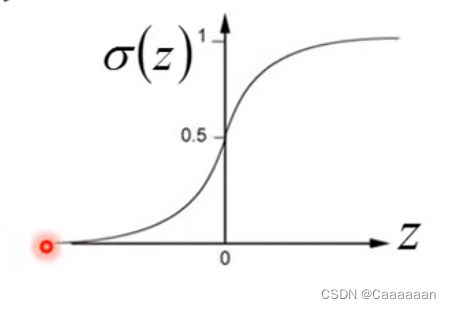

P ( C 1 ∣ x ) = σ ( w ∗ x + b ) P(C_1|x)=\sigma(w*x+b) P(C1∣x)=σ(w∗x+b)
而你会发现,你在生成模型这里,我们需要从训练集中估计出N1,N2, μ 1 \mu^1 μ1 , μ 2 \mu^2 μ2, Σ \Sigma Σ ,然后去拥有 w 和 b
那么我们为什么不直接找到w 和 b呢?
——w是一个vector
——敬请期待下一章
——逻辑斯特回归























 4301
4301











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










