超超超超超简单推导CNN反向传播——低调学习CNN(1)

1.写在前面

相信诸位老铁，点开我这篇博客，都是想看看卷积层的反向传播和池化层的反向传播是怎么求导的，但是点开其他博客都是一大段的公式，望而止步，我之前也是介个样子。

在本次博客，我先带大家感觉一下求导的过程，严格来说，本次的CNN并非正宗的CNN，但是却可以帮助我们了解求导的过程！大家一定要看懂这一步，再看下一步，必要的时候拿出纸和笔好好算算！！

笔者在前向传播的时候，会顺便将一些导数求出，以备之后使用。

2.卷积过程

注:

• $A_{m\times n}$矩阵与$B_{x\times y}$矩阵(做步长$stride=1的$)$valid$卷积操作($m\ge x且n\ge y$)
  所得元素维度为$(m-x+1)\times (n-y+1)$
• 当卷积操作的步长为$stride$时，卷积的输出矩阵为$(\frac{m-x}{strid{e}_x}+1)\times (\frac{n-y}{strid{e}_y}+1)$，当其中不能整除时，说明该步长不适合卷积操作
• 如果我们还有$zeroPadding$，则需要加上$Padding$数字，一般来说输出矩阵为$(\frac{m-x+2p_x}{strid{e}_x}+1)\times (\frac{n-y+2p_y}{strid{e}_y}+1)$
• 严格的来说，是$([\frac{m-x+2p_x}{strid{e}_x}]+1)\times ([\frac{n-y+2p_y}{strid{e}_y}]+1)$
• 同时卷积核也叫做感受野($receptivefield$)

相信这个操作，大家都熟悉的一批，我不赘述了(为了不用别人的图，这么个小破gif花了好久哈哈)

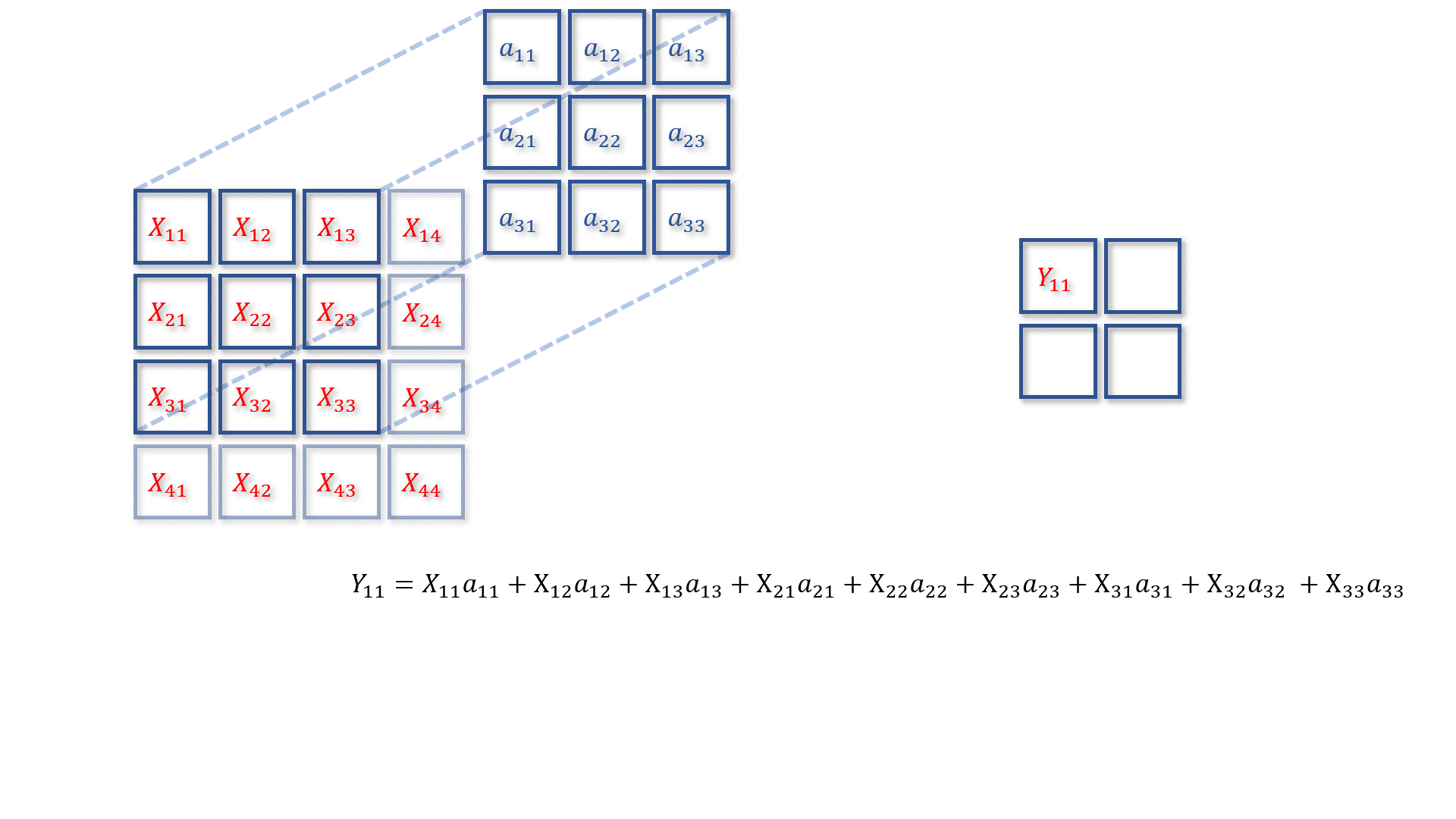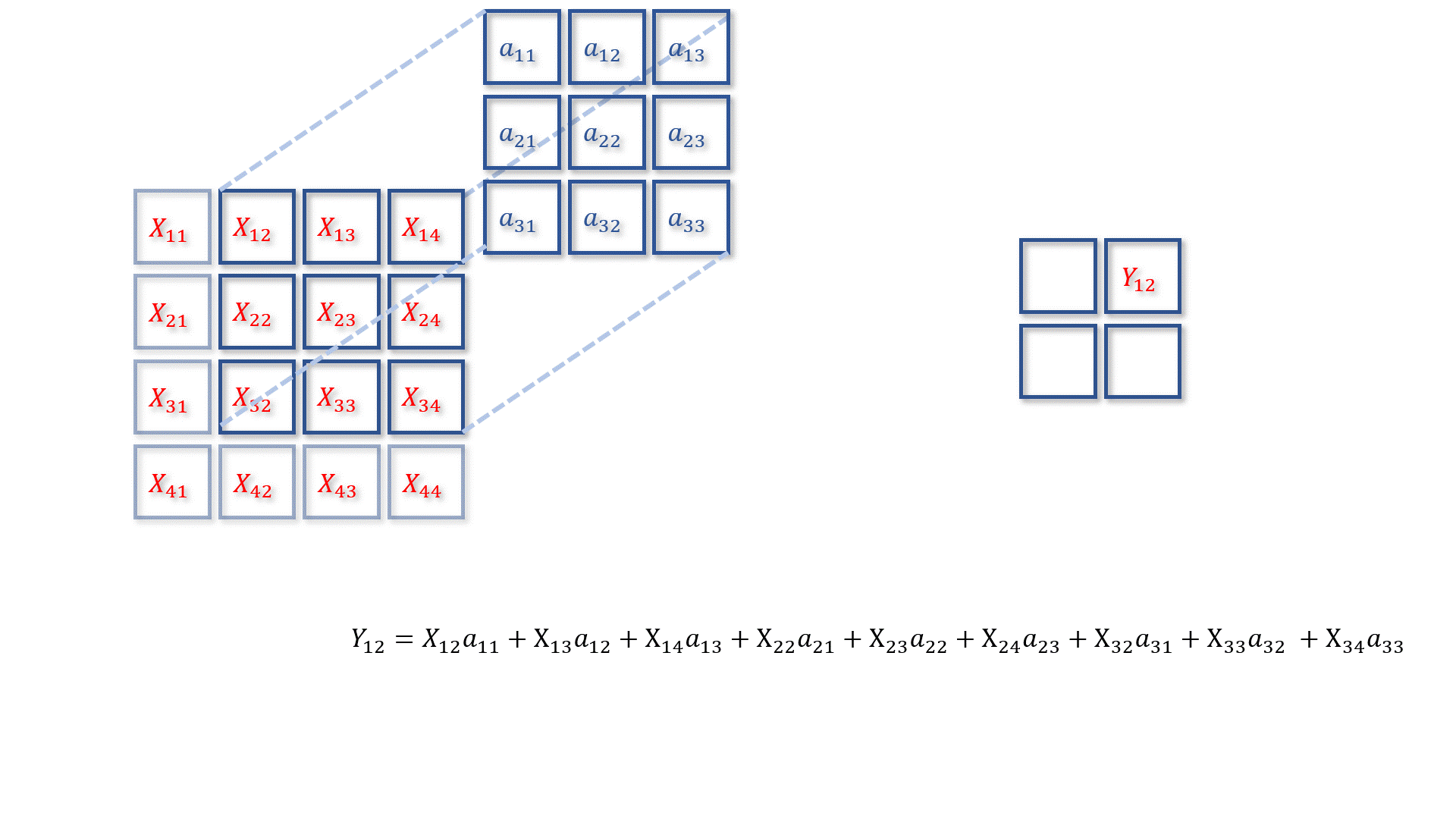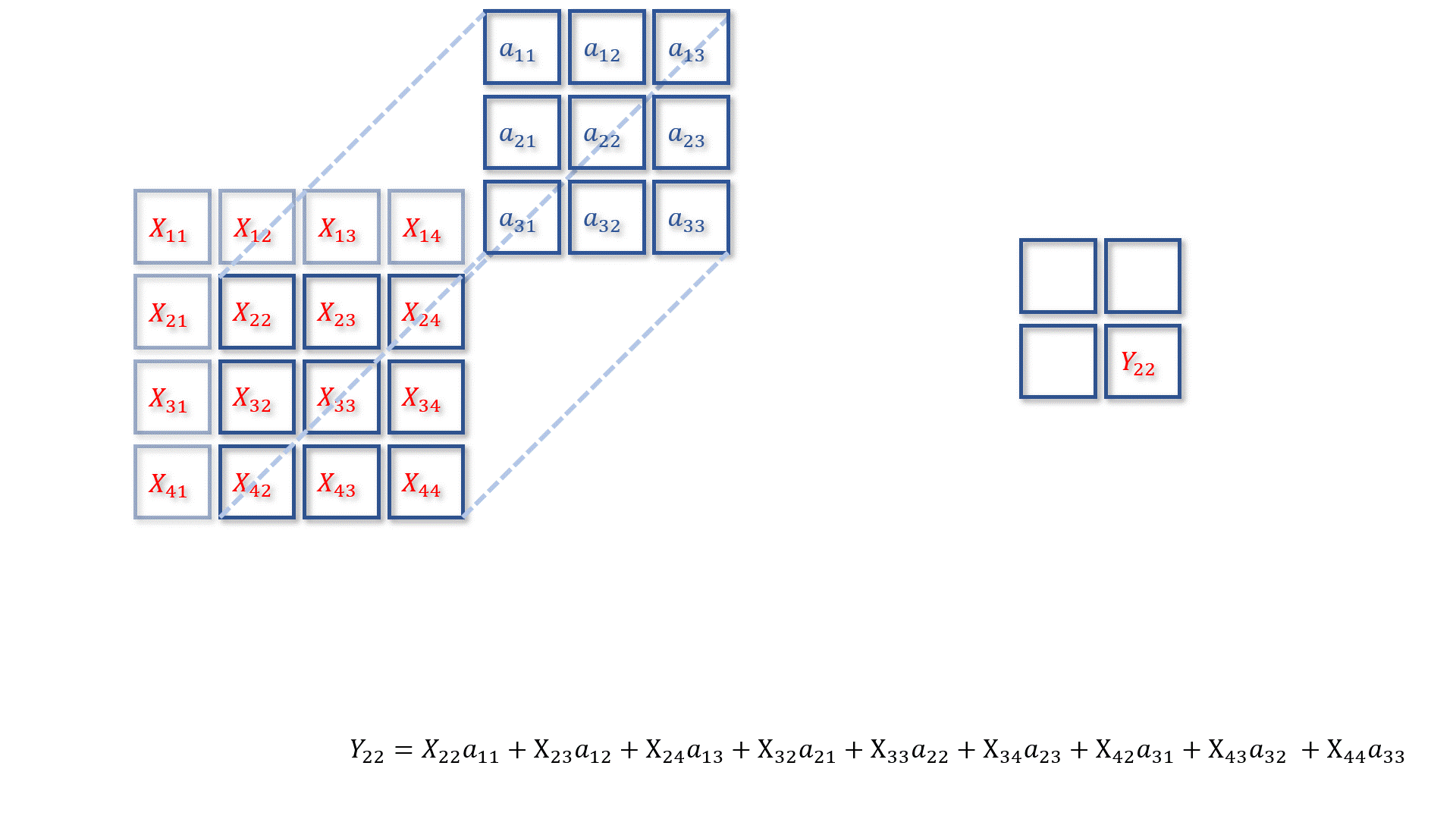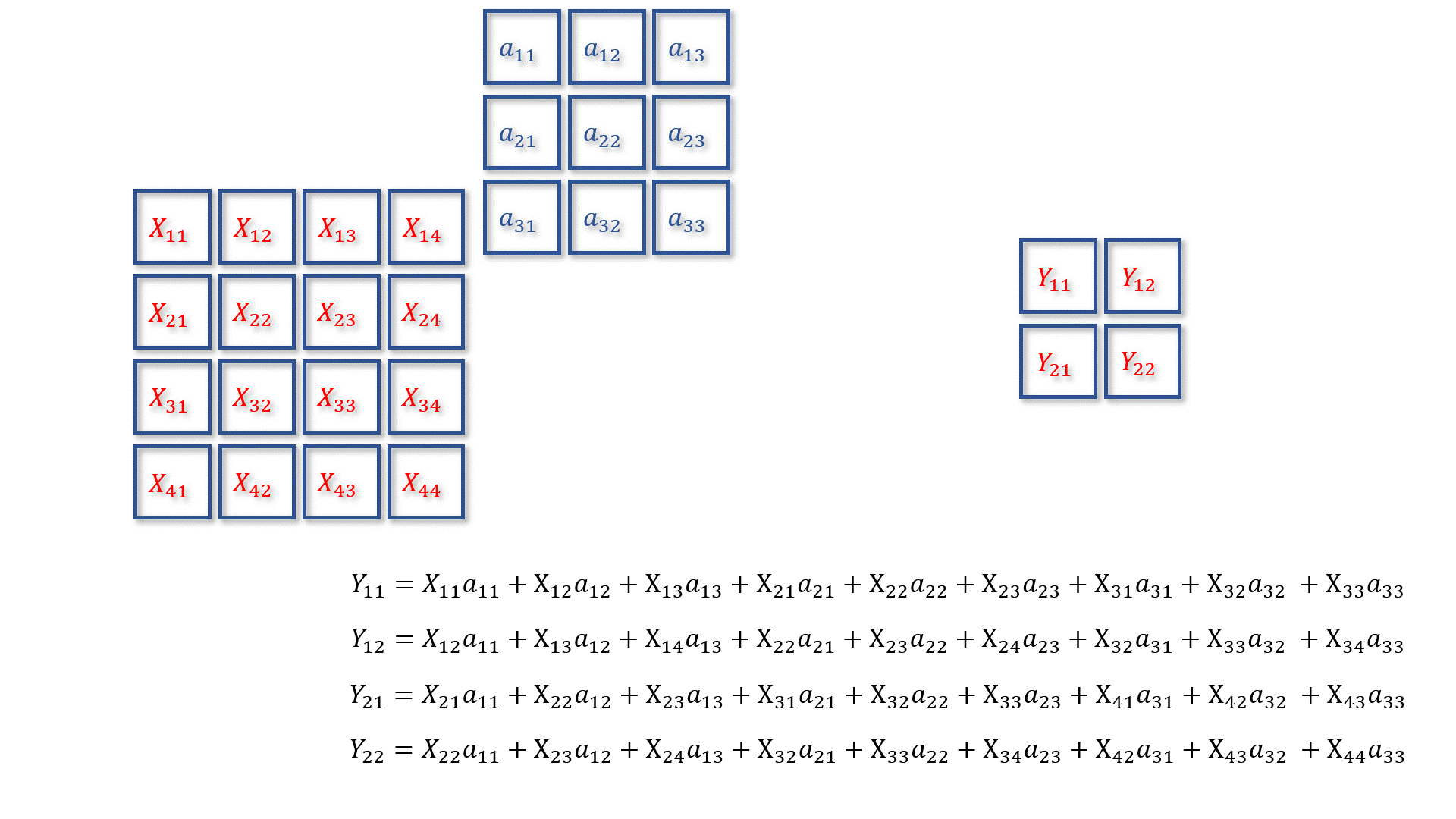
卷积核$A$对$X$进行卷积操作，得到矩阵$Y$：

在这里我们先让$Y_{11}$、$Y_{12}$、$Y_{13}$和$Y_{14}$分别对$A$矩阵中的$a_{11}$和$a_{12}$元素求偏导，得到以下结果：

其实，$Y_{11}$、$Y_{12}$、$Y_{13}$和$Y_{14}$对矩阵$A$中的其他元素求偏导，也会得到类似的结果，老铁们先不要急，一会告诉大家规律。

3.池化操作($Pooling$或$downsample$降采样)

再得到矩阵$Y$后，我们对其进行池化(Pooling)操作，不失一般性，可以看做$B$矩阵对矩阵$Y$做卷积操作，得到矩阵$Z$，可以将其视为单元素矩阵$Z$，也可以将其视为一个数$Z$，不过这里不影响：
实际上，池化操作，可以视为没有参数

令$Z$分别对矩阵$Y$元素$Y_{11}$、$Y_{12}$、$Y_{13}$和$Y_{14}$求偏导，有图右下角式子:

4.求出误差

我们得出了预测值$Z$，原有真实值为$R$，采用均方误差$E=\frac{1}{2}(Z-R{)}^2$
令误差$E$对$Z$求导数:
$$\frac{\partial E}{\partial Z}=Z-R$$
有:
$$\frac{\partial E}{\partial a_{11}}=(Z-R)\frac{\partial Z}{\partial a_{11}}$$

5.反向传播求偏导

此时，我们令$Z$对矩阵$A$中元素$a_{11}$和$a_{12}$求导，同时带入我们之前求的偏导数:


$Z$对$A$中其他元素求偏导结果类似(大家最好动手算一算，这波不亏的)：

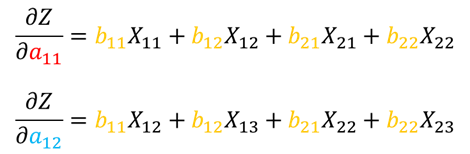
可以看出，不论是$Z$对$A$中哪一项元素求偏导，都会有$b_{11}、b_{12}、b_{21}和b_{22}$，那我们现在关心一下，偏导中矩阵$X$的元素：

你现在可以大胆的猜测一下，$\frac{\partial Z}{\partial a_{13}}$等于什么？

没错，就是矩阵$X$右上角的4个元素和矩阵$B$的四个元素相乘再相加。

不妨再大胆的猜一下，矩阵$Z$对矩阵$A$求偏导等于什么？

等于，矩阵$X$与矩阵$B$做$valid$卷积操作，刚好是$3\times 3=9$个元素

即：$\frac{\partial Z}{\partial A}=X\ast B$

所以：$\frac{\partial E}{\partial A}=(Z-R)\times X\ast B$

OK! 咱们求导工作到此结束！是不是感觉很清楚呢？？😝

---

注：严格来说，本次博客所有的$卷积操作$，都应该叫做$相关操作$！
若之后有时间，我再写写二者的区别和联系