读这篇上古年代的文章
Compressing Convolutional Neural Networks in the Frequency Domain
先将参数映射到频域,然后建立参数共享机制
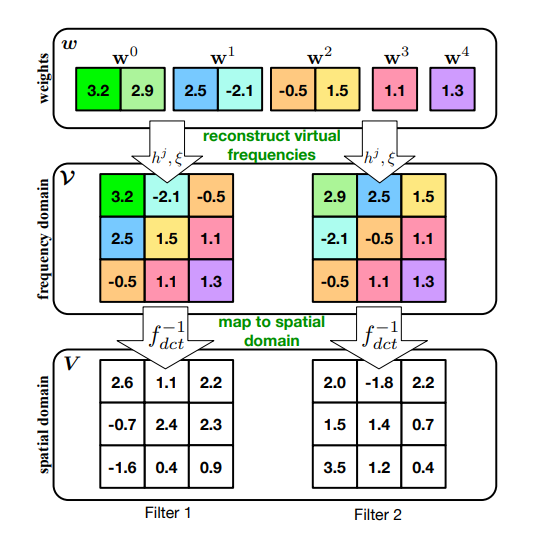
文中用到了DCT, 这里来回忆一下
1. 一维离散傅里叶变换
X ( k ) = D F T [ x ( n ) ] = ∑ n = 0 N − 1 x ( n ) e − j 2 π k n N X(k) = DFT \left [ x \left (n \right ) \right ] =\sum^{N-1}_{n=0} x(n) e ^ { -j \frac{2\pi kn}{N} } X(k)=DFT[x(n)]=n=0∑N−1x(n)e−jN2πkn
x ( n ) x(n) x(n) 为时域离散信号, N N N为时域离散信号的点数
将幂指数部分使用欧拉公式展开
X ( k ) = ∑ n = 0 N − 1 x ( n ) ( c o s ( 2 π k n N ) − j s i n ( 2 π k n N ) ) X(k) = \sum_{n=0}^{N-1} x(n) \left( cos \left ( \frac{2\pi k n}{N} \right ) -j sin \left ( \frac{2\pi k n}{N} \right ) \right ) X(k)=n=0∑N−1x(n)(cos(N2πkn)−jsin(N2πkn))
X ( k ) = ∑ n = 0 N − 1 x ( n ) c o s ( 2 π k n N ) − j ∑ n = 0 N − 1 x ( n ) s i n ( 2 π k n N ) X(k) = \sum_{n=0}^{N-1} x(n) cos \left ( \frac{2\pi k n}{N} \right ) -j \sum_{n=0}^{N-1} x(n) sin \left ( \frac{2\pi k n}{N} \right ) X(k)=n=0∑N−1x(n)cos(N2πkn)−jn=0∑N−1x(n)sin(N2πkn)
实部是偶函数,虚部是奇函数,变量是
k
k
k,
n
n
n和
x
(
n
)
x(n)
x(n)为常量
R
e
a
l
(
X
(
k
)
)
=
∑
n
=
0
N
−
1
x
(
n
)
c
o
s
(
2
π
k
n
N
)
Real \left( X(k) \right ) = \sum_{n=0}^{N-1} x(n) cos \left ( \frac{2\pi k n}{N} \right )
Real(X(k))=n=0∑N−1x(n)cos(N2πkn)
I m a g ( X ( k ) ) = − ∑ n = 0 N − 1 x ( n ) s i n ( 2 π k n N ) Imag \left( X(k) \right ) = -\sum_{n=0}^{N-1} x(n) sin \left ( \frac{2\pi k n}{N} \right ) Imag(X(k))=−n=0∑N−1x(n)sin(N2πkn)
假设原信号
x
(
n
)
x(n)
x(n)是一个全是实数的偶函数信号
I
m
a
g
(
X
(
k
)
)
=
0
Imag \left( X(k) \right ) = 0
Imag(X(k))=0
则
X
(
k
)
=
∑
n
=
0
N
−
1
x
(
n
)
c
o
s
(
2
π
k
n
N
)
X(k) = \sum_{n=0}^{N-1} x(n) cos \left ( \frac{2\pi k n}{N} \right )
X(k)=n=0∑N−1x(n)cos(N2πkn)
(以上便是DCT变换的核心思想)
DCT实际上就是限定了输入信号的DFT变换,最常用的DCT变换:
F ( u ) = c ( u ) ∑ x = 0 N − 1 f ( x ) c o s ( ( x + 0.5 ) π N u ) F(u) = c(u) \sum_{x=0}^{N-1}f(x) cos \left( \frac{(x+0.5)\pi}{N} u \right) F(u)=c(u)x=0∑N−1f(x)cos(N(x+0.5)πu)
c ( u ) = { 1 N , u = 0 2 N , u ≠ 0 c(u) = \left\{\begin{matrix} \sqrt{\frac{1}{N}}, & u=0\\ \sqrt{\frac{2}{N}}, & u\neq 0 \end{matrix}\right. c(u)=⎩ ⎨ ⎧N1,N2,u=0u=0
- DFT是对信号进行周期拓展,DCT是对信号进行先镜像然后再周期拓展,这样做的好处在于拓展的信号间实现了平滑的过渡。
- 而直接周期拓展会出现跳变,这种跳变在频域对应着高频的分量
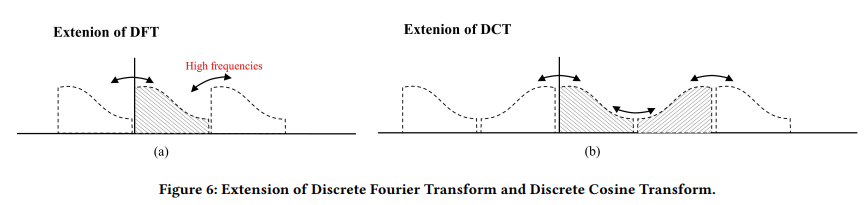
图片摘自:
FECAM: Frequency Enhanced Channel Attention Mechanism for Time Series Forecasting
2. 公式证明
DCT要求原始变换信号是一个实偶函数,但实际应用中并没有那么多实偶函数,于是需要从离散信号构造出实偶函数:
- 设一个实数离散信号 x [ 0 ] , x [ 1 ] , x [ 2 ] , . . . , x [ N − 1 ] {x[0], x[1], x[2], ..., x[N-1]} x[0],x[1],x[2],...,x[N−1]
- 将长度扩大到 2 N 2N 2N倍,定义新信号 x ′ [ m ] x'[m] x′[m]
x ′ [ m ] = x [ m ] ( 0 ≤ m ≤ N − 1 ) x ′ [ m ] = x [ − m − 1 ] ( − N ≤ m ≤ − 1 ) \begin{aligned} x'[m] &= x[m] & (0 \le m \le N-1) \\ x'[m] &= x[-m-1] & (-N \le m \le -1) \end{aligned} x′[m]x′[m]=x[m]=x[−m−1](0≤m≤N−1)(−N≤m≤−1)
X ( k ) = ∑ m = − N N − 1 x ′ [ m ] e − j 2 π m k 2 N X(k) = \sum_{m=-N}^{N-1} x'[m] e ^ { \frac{ -j2\pi m k }{\bf{2N}} } X(k)=m=−N∑N−1x′[m]e2N−j2πmk
4 1 5 2 2 5 1 5 <----- value
-4 -3 -2 -1 0 1 2 3 <----- index
当前关于 m = − 1 2 m=-\frac{1}{2} m=−21 对称,所以向右平移
X ( k ) = ∑ m = − N + 1 2 N − 1 2 x ′ [ m − 1 2 ] e − j 2 π m k 2 N = ∑ m = − N + 1 2 N − 1 2 x ′ [ m − 1 2 ] c o s ( 2 π m k 2 N ) = 2 ∑ m = 1 2 N − 1 2 x ′ [ m − 1 2 ] c o s ( 2 π m k 2 N ) \begin{aligned} X(k) &= \sum_{m=-N+\frac{1}{2}}^{N-\frac{1}{2}} x'[m-\frac{1}{2}] e ^ { \frac{ -j2\pi m k }{\bf{2N}} } \\ &= \sum_{m=-N+\frac{1}{2}}^{N-\frac{1}{2}} x'[m-\frac{1}{2}] cos \left ( \frac{ 2\pi m k }{2N} \right ) \\ &= 2 \sum_{m=\frac{1}{2}}^{N-\frac{1}{2}} x'[m-\frac{1}{2}] cos \left ( \frac{ 2\pi m k }{2N} \right ) \end{aligned} X(k)=m=−N+21∑N−21x′[m−21]e2N−j2πmk=m=−N+21∑N−21x′[m−21]cos(2N2πmk)=2m=21∑N−21x′[m−21]cos(2N2πmk)
令 n = m − 1 2 n=m-\frac{1}{2} n=m−21,有
X ( k ) = 2 ∑ m = 1 2 N − 1 2 x ′ [ m − 1 2 ] c o s ( 2 π m k 2 N ) = 2 ∑ m = 0 N − 1 x ′ [ n ] c o s ( π ( n + 1 2 ) k N ) \begin{aligned} X(k) &= 2 \sum_{m=\frac{1}{2}}^{N-\frac{1}{2}} x'[m-\frac{1}{2}] cos \left ( \frac{ 2\pi m k }{2N} \right ) \\ &= 2 \sum_{m=0}^{N-1} x'[n] cos \left ( \frac{ \pi (n+\frac{1}{2}) k }{N} \right ) \\ \end{aligned} X(k)=2m=21∑N−21x′[m−21]cos(2N2πmk)=2m=0∑N−1x′[n]cos(Nπ(n+21)k)




















 8945
8945











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








