机器学习、深度学习必备数学基础之线性代数篇

最新推荐文章于 2022-12-05 16:14:38 发布

偷偷玩两下

最新推荐文章于 2022-12-05 16:14:38 发布

阅读量636

点赞数 1

分类专栏： Python 机器学习深度学习文章标签：数学基础

本文链接：https://blog.csdn.net/HeyShHeyou/article/details/103770318

版权

Python 同时被 3 个专栏收录

17 篇文章 2 订阅

订阅专栏

机器学习

4 篇文章 0 订阅

订阅专栏

深度学习

1 篇文章 0 订阅

订阅专栏

一. 标量

标量仅用于表达值的大小，也称作零阶张量。一般小写变量名标识，例：符号 x ∈ R 表示标量 x 属于实数值数组 R。

Python 中内置了少数几种标量类型，如 int，float，complex，bytes，Unicode。而在 Python 库 NumPy 中，有 24 种新的基本数据类型来描述不同类型的标量。

判断标量：

import numpy as np
print(np.isscalar(3.3))	        # True
print(np.isscalar([3.3]))	# False

二. 向量

向量是由多个单个数字组成的有序数组，也称作一阶张量。向量是向量空间中的片段。向量空间则可以被认为是在特定长度（或维度）中所有可能存在的向量集合。我们通常说的现实世界中的三维空间，在数学里可以用向量空间表达为 $R^{3}$ 。

为了清晰明确地标示向量中的必要成分，向量中的第 i 个标量元素被记做 x[i] 。

在深度学习中，向量通常表示特征向量，它的原始成分则表示特定特征的相关程度。

向量的常见表达式一般如下：

$X=\begin{bmatrix} x_{1}\\ x_{2}\\ x_{3}\\ ...\\ x_{n}\\ \end{bmatrix}$

基本的向量操作：

x=[1,2,3]
y=[4,5,6]
print(type(x))  # <class 'list'>
print(x+y)      # [1, 2, 3, 4, 5, 6]

z=np.add(x,y)
print(z)        # [5 7 9]
print(type(z))  # <class 'numpy.ndarray'>

mul=np.cross(x,y)
print(mul)      # [-3  6 -3]

注：np.cross() 方法为计算两个向量的外积，也叫做叉乘。在 numpy 的源码中，关于叉乘的介绍如下：

The cross product of `a` and `b` in :math:`R^3` is a vector perpendicular to both `a` and `b`. If `a` and `b` are arrays of vectors, the vectors are defined by the last axis of `a` and `b` by default, and these axes
can have dimensions 2 or 3. Where the dimension of either `a` or `b` is 2, the third component of the input vector is assumed to be zero and the cross product calculated accordingly. In cases where both input vectors
have dimension 2, the z-component of the cross product is returned.

概括地说，两个向量的外积，又叫叉乘、叉积向量积，其运算结果是一个向量而不是一个标量。并且两个向量的外积与这两个向量组成的坐标平面垂直。（向量的点积与叉积在学生时代的线性代数中曾学过，看到公式才能回想起来...）

假设向量 a，b 如下：

则 a 与 b 的叉乘结果为：

其中：

三. 矩阵

矩阵是由数字构成的矩形阵列，也称作二阶张量。若 m 和 n 为正整数（ m，n ∈ N ），则 m × n 的矩阵中包含 m * n 个元素，由m 行和 n 列构成。例如 m × n 矩阵可写做：

$X=\begin{bmatrix} x_{11} & x_{12} & ... & x_{1n} \\ x_{21} & x_{22} & ... & x_{2n} \\ x_{31} & x_{32} & ... & x_{3n} \\ ... & ... & ... & ... \\ x_{m1} & x_{m2} & ... & x_{mn} \end{bmatrix}$

矩阵在实际应用非常重要！例如有 m 个用户，每个用户有 n 个特征，对应的就是 m*n 的矩阵，例如在推荐系统中，基于用户或商品的协同过滤算法，构造一个矩阵，每一行代表一个用户，每一列代表一部电影，用户与电影对应的矩阵元素则是用户对该电影的评分。详细参考：协同过滤算法----电影推荐系统

通常以上矩阵的表达式简写如下：

$X= \left [ x_{ij} \right ]_{mn}$

在 Python 中一般使用 numpy 库创建与操作 n 维的数组，基本操作如下：

创建矩阵、矩阵之间加法、矩阵之间乘法、矩阵与标量的加法、矩阵与标量的乘法、矩阵转置。

## 1. 创建矩阵
x = np.matrix([[1,2],[2,3],[3,4]])
print(x)
# [[1 2]
#  [2 3]
#  [3 4]]

print(x.shape)    #(3, 2)   # 矩阵维度，3行2列


## 2. 矩阵之间加法
y = np.matrix([[1, 2], [3, 4]])
sum = y.sum()
print(sum)  # 10    # 计算矩阵中所有元素之和，返回标量

sum2 = np.add([1, 2, 3], [4, 5, 6])
print(sum2)  # [5 7 9]  # 两个矩阵对应位置相加，返回矩阵


## 3. 矩阵之间的乘法
y1 = np.matrix([[1, 2], [3, 4]])
y2 = np.matrix([[5, 6], [7, 8]])
print(np.dot(y1, y2))
# [[19 22]
#  [43 50]]

print(y1 * y2)  # 对于数组 np.array()：对应元素相乘；对于矩阵 np.matrix()：计算矩阵乘积
# 数组：
# [[ 5 12]
#  [21 32]]
# 矩阵：
# [[19 22]
#  [43 50]]

print(np.multiply(y1, y2))  # 对应元素相乘
# [[ 5 12]
#  [21 32]]


## 4. 矩阵与标量的加法
sum3 = np.matrix([[1, 2], [3, 4]])
print(sum3 + 1)    # 对应位置相加
# [[2 3]
#  [4 5]]


## 5. 矩阵与标量的乘法
sum4 = np.matrix([[1, 2], [3, 4]])
print(sum4 * 2)    # 对应位置相乘
# [[2 4]
#  [6 8]]


## 6. 矩阵转置
a = np.array([[1,2],[3,4]])
print(a)
# [[1 2]
#  [3 4]]

print(a.transpose())
# [[1 3]
#  [2 4]]

矩阵相乘图解

当 m x n 的矩阵 A 与 n x p 的矩阵 B 相乘，得到 m x p 的矩阵 C，对应乘法如图：

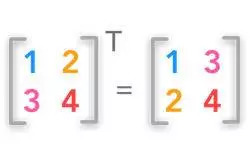
矩阵的转置图解

矩阵的转置可以使一个行向量变成一个列向量，或反方向操作亦成立作亦成立。可以通俗的理解成沿着对角线对折交换。

四、张量

在几何代数中，张量的定义是基于向量和矩阵的推广，通常用来表示广泛的数据类型。上面也提到，标量是零阶张量，矢量是一阶张量，矩阵是二阶张量。

举个例子，对于任意一张图片，都可以用三阶张量表示，其中对应的三个维度分别是图片的高度、宽度和色彩数据。用张量表示图片，对应如下：

其中，表的横轴表示图片的宽度，从0至319个像素点。表的纵轴表示图片的高度，这里只截取从0至4个像素点。表格中每个方格代表一个像素点，比如第一行第一列的表格数据为[1.0,1.0,1.0]，代表 RGB 三原色在图片的这个像素点中的取值，也即R=1.0，G=1.0，B=1.0。

对于常见的公用数据集类型总结如下：
0维：一个标量   width   零阶张量
1维：一个向量   [width] 一阶张量
2维：一个矩阵   [width, height] 二阶张量
3维：一张图片 [width, height, color_data] 三阶张量，三个维度分别是图片的高度、宽度和色彩数据
4维：一段视频   [width, height, color_data, frames] 四阶张量，四个维度分别是图片的高度、宽度、色彩数据、帧数

注：张量的阶级对应其维数。维度的扩张可以用下图表示。

张量是深度学习中一个非常基础并且重要的概念，它不仅是深度学习框架中的一个核心部分，并且在后续的运算和优化算法中几乎都是基于张量操作的。

五、范数

范数(norm)是数学中的一种基本概念。它常常被用来度量某个向量空间（或矩阵）中的每个向量的长度或大小。在线性代数、泛函分析及相关的数学领域，范数是一个函数，是矢量空间内的所有矢量赋予非零的正长度或大小。

复习下初等数学的知识，一个向量的长度定义为向量中每个元素平方和的平方根，比如向量 p = (3,4) 的模长是5，其中，模长5就是向量 p 的一种 L2 范数，除此之外，向量的范数还包括 L0 范数、L1 范数、L2 范数和 L∞ 范数，所有的这些范数统筹为 LP 范数，下面逐一介绍。

1. LP 范数：

LP 范数不是一个范数，而是一组范数的集合，这一点与闵可夫斯基距离的定义一样。

若向量 X = (x1, x2, …, xn)，则 LP 范数定义如下：

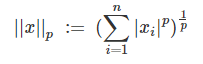
当 p=0 时，LP 范数转换为 L0 范数；

当 p=1 时，LP 范数转换为 L1 范数，也称作曼哈顿距离，它在R2空间中的单位圆是正方形；

当 p=2 时，LP 范数转换为 L2 范数，它在R2空间中的单位圆是圆形；

当 p=∞ 时，LP 范数转换为 L∞ 范数，它是R2空间中的单位圆也是一个正方形。

关于 Lp 范数的几何解释可以用单位圆来说明。单位圆是无穷个向量终点组成的集合，这些向量必须满足 Lp 范数为1且起点为原点。对于任何p范数，它是一个超椭圆（具有全等轴）。下面图为p取不同数值，Lp 范数对应的单位圆。

2. L0 范数：

当 p = 0 时，则向量 X 的 L0 范数定义为向量 X 中所有非零元素的个数。

例如，当向量 X = (0, 1, 2)，向量中有1个元素为0，2个非零元素 (1和2)，则向量 X 对应 L0 范数为 2。

由于 L0 范数表示向量中非零元素的个数，这个属性非常适用于机器学习中的稀疏编码。在特征选择中，通过最小化 L0 范数来寻找最少和最优的稀疏特征项。

但是，L0 范数的最小化问题是 NP 难问题（L0 范数很难优化求解）。而 L1 范数是 L0 范数的最优凸近似，它比 L0 范数要更容易求解。因此，优化过程将会被转换为更高维的范数（例如 L1 范数或 L2 范数）问题。

3. L1 范数：

当 p=1 时，LP 范数转换为 L1 范数，此时也称作曼哈顿距离。

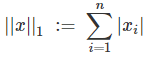
例如，若向量 X = (0, 1, 2)，则 X 对应 L1 范数为 |0| + |1| + |2| = 1 + 2 = 3。

简单的说，L1 范数就是向量中各个元素绝对值之和，也被称作 “Lasso regularization”（稀疏规则算子）。

在机器学习特征选择中，稀疏规则化能够实现特征的自动选择。

一般来说，输入向量X的大部分元素（也就是特征）都是和最终的输出Y没有关系或者不提供任何信息的，在最小化目标函数的时候考虑这些额外的特征，虽然可以获得更小的训练误差，但在预测新的样本时，这些没用的信息反而会被考虑，从而干扰了对正确Y的预测。

稀疏规则化算子的引入就是为了完成特征自动选择，它会学习地去掉这些没有信息的特征，也就是把这些特征对应的权重置为 0，从而有利于特征选择。

L0 范数与 L1 范数都可以实现稀疏，而 L1 范数比 L0 具有更好的优化求解特性而被广泛使用。 L0 范数本身是特征选择的最直接的方案，但因其很难优化求解，因此实际应用中使用 L1 来得到 L0 的最优凸近似。

总结：L1 范数和 L0 范数可以实现稀疏，L1 因为拥有比 L0 更好的优化求解特性而被广泛应用。

注：尽管最小化目标向量的 L1 范数求解比最小化目标向量的 L0 范数容易，可通过最优化算法得到对应的可行解。但是 L1 范数的导数不易求，所以许多机器学习问题中遇到 L1 范数最小化问题会转为 L2 范数最小化问题。

4. L2 范数：

当 p=2 时，LP 范数转换为 L2 范数，这应该是范数系列中最常用的范数，此时也称作欧氏距离。

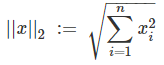
例如，若向量 X = (2, 3, 6)，则 X 对应 L2 范数为

$||X||_{2} = \sqrt{2^{2}+3^{2}+6^{2}} = \sqrt{4+9+36} = \sqrt{49} = 7$

L2 范数的本质是指向量各元素的平方和然后求平方根。如果我们让 L2 范数的规则项最小，可以使得每个元素都很小，都接近于0，但与 L1 范数不同，它不会让它等于0，而是接近于0。而越小的参数说明模型越简单（因为限制了参数很小，实际上就限制了多项式某些分量的占比很小、影响很小，这样就相当于减少了参数的个数），越简单的模型则越不容易产生过拟合现象。所以，在机器学习中，L2 范数被广泛的应用在解决过拟问题。

总结：通过 L2 范数限制模型空间的复杂程度，从而在一定程度上避免过拟合。

优点：

1. 防止过拟合，提升模型的泛化能力。

2. 优化求解变得稳定和快速。

5. L∞ 范数

当 p=∞ 时，LP 范数转换为 L∞ 范数。

若向量 X = (0, 1, 2)，则 X 对应 L∞ 范数为 max(0, 1, 2) = 2。

六、特征分解

特征分解是线性代数中非常重要的概念，主要是把特征矩阵分解为一组特征向量和特征值表示矩阵之积的方法。需要注意只有对可对角化矩阵才可以进行特征分解！

先来看下基本的数学定义。如果说 N 维非零向量 v 是 N×N 的矩阵 A 的特征向量，当且仅当下式成立：

Av = λv

其中 λ 是标量，称为 v 对应的特征值，也称为特征值 λ 对应的特征向量。

此时，矩阵 A 可以被分解为以下形式：

其中 Q 是 N×N 矩阵，且其第 i 列为 A 的特征向量。 Λ 是对角矩阵，其对角线上的元素为对应的特征值，也即 Λ ii=λi。

这里需要注意只有可对角化矩阵才可以作特征分解。比如 $\begin{bmatrix} 1 &1 \\ 0 & 1 \end{bmatrix}$ 不能被对角化，也就不能特征分解。

对于特征分解公式本身来说，可理解为向量 v 在几何空间中经过矩阵 A 的变换后得到向量 λv。所以，向量 v 经过矩阵 A 变换后，本身的方向没有发生变化，只是伸缩了 λ 倍。

特征值分解主要是为了获取矩阵的特征值与特征向量，其中特征值表示该特征的重要程度，而特征向量表示该特征的内容，可以将每一个特征向量理解为一个线性的子空间。不过，特征值分解也有很多的局限，比如说变换的矩阵必须是方阵（可对角化矩阵）。

另外，虽然对于任意一个对角化矩阵 A，都可以对其进行特征分解，但是结果可能不唯一。例如，当多个特征向量拥有相同的特征值，那么由这些特征向量产生的生成子空间中，任意一组正交向量都是该特征值对应的特征向量。因此，我们可以等价的从这些特征向量中构成 Q 作为替代。按照惯例，我们通常按降序排列 Λ 中的元素。在该约定下，特征分解唯一当且仅当所有的特征值都是唯一的。

七、奇异值分解 SVD

在特征分解时说道，矩阵的特征分解是有前提条件的，那就是只有对可对角化的矩阵才可以进行特征分解。但实际中很多矩阵并不是可对角化的矩阵，甚至很多矩阵都不是方阵（即矩阵的行列数目不相等）。例如，M 个用户，每个用户具有 N 维的特征，得到的矩阵就是 M * N 矩阵。

此时，可以将特征分解在任意矩阵上进行推广，得到了一种叫作 “矩阵的奇异值分解” 的方法，简称 SVD。通过奇异分解，我们可以简化运算，得到一些类似特征分解的信息。

奇异值分解的具体做法是将一个普通矩阵分解为奇异向量和奇异值。例如矩阵 A 可以分解成三个矩阵的乘积：

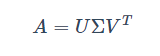
假设 A 是一个 M * N 矩阵，那么 U 是一个 M * M 矩阵，Σ 是一个 M * N 矩阵，V 是一个 N * N 矩阵。

其中，每个矩阵都拥有特殊的结构：U 和 V 都是正交矩阵，Σ 是对角矩阵（不一定是方阵）。对角矩阵 Σ 对角线上的元素被称为矩阵 A 的奇异值。矩阵 U 的列向量被称为左奇异向量，矩阵 V 的列向量被称右奇异向量。

几何含义：对于任何的一个矩阵，我们要找到一组两两正交单位向量序列，使得矩阵作用在此向量序列上后得到新的向量序列保持两两正交。

奇异值分解最有用的一个性质可能是拓展矩阵求逆到非方矩阵上。另外，SVD 可用于推荐系统中的协同过滤算法。

参考链接

https://www.cnblogs.com/abella/p/10142935.html

https://www.cnblogs.com/lzhu/p/10405091.html

http://www.cnbruce.com/blog/showlog.asp?log_id=1423

https://blog.csdn.net/zouxy09/article/details/24971995/

https://www.cnblogs.com/Kalafinaian/p/11143995.html

https://blog.csdn.net/m0_37673307/article/details/82317696

偷偷玩两下

关注

1
点赞
踩
5

收藏

觉得还不错? 一键收藏
0
评论
机器学习、深度学习必备数学基础之线性代数篇

一. 标量标量仅用于表达值的大小，也称作零阶张量。一般小写变量名标识，例：符号 x ∈ R表示标量 x 属于实数值数组 R。Python 中内置了少数几种标量类型，如 int，float，complex，bytes，Unicode。而在 Python 库 NumPy 中，有 24 种新的基本数据类型来描述不同类型的标量。判断标量：import numpy as npprint...
复制链接

扫一扫