Paper Notes: Graph Attention Networks

Graph Attention Networks

• LINK: https://arxiv.org/abs/1710.10903

• CLASSIFICATION: SPATIAL-BASED GCN

• YEAR: Submitted on 30 Oct 2017 (v1), last revised 4 Feb 2018 (this version, v3)

• FROM: ICLR 2018

• WHAT PROBLEM TO SOLVE: To overcome the limitations of GCNs.

• SOLUTION: By stacking layers in which nodes are able to attend over their neighborhoods’ features, we enable (implicitly) specifying different weights to different nodes in a neighborhood, without requiring any kind of costly matrix operation (such as inversion) or depending on knowing the graph structure upfront.

• CORE POINT:

  • Serveral interestring properties of attention architecture

    1. The operation is efficient, since it is parallelizable across node-neighbor pairs.
    2. It can be applied to graph nodes having different degrees by specifying arbitrary weights to the neighbors.
    3. The model is directly applicable to inductive learning problems, including tasks where the model has to generalize to completely unseen graphs.

  • Graph Attentional layer

    1. a shared linear transformation, parametrized by a weight matrix, $W\in R^{F\prime \times F}$ , is applied to every node. We then perform self-attention on the nodes—a shared attentional mechanism $a:R^{F\prime }\times R^{F\prime }\to R$ computes attention coefficients. That indicate the importance of node j’s features to node i. The attention mechanism a is a single-layer feedforward neural network.

       

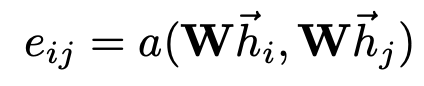
    2. We inject the graph structure into the mechanism by performing masked attention—we only compute eij for nodes $j\in N_i$, where Ni is some neighborhood of node i in the graph. In all our experiments, these will be exactly the first-order neighbors of i (including i). To make coefficients easily comparable across different nodes, we normalize them across all choices of j using the softmax function:

       

    3. Parametrized by a weight vector$\vec{a}\in R^{2F\prime }$ , and applying the LeakyReLU nonlinearity (with negative input slope α = 0.2).

       

    4. To stabilize the learning process of self-attention, we have found extending our mechanism to employ multi-head attention to be beneficial.

       

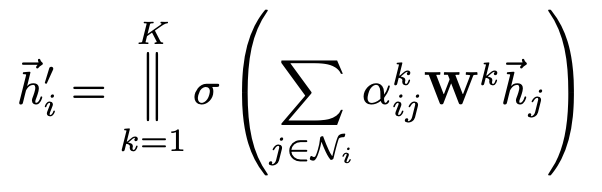
    5. Specially, if we perform multi-head attention on the final (prediction) layer of the network, concatenation is no longer sensible—instead, we employ averaging, and delay applying the final nonlinearity (usually a softmax or logistic sigmoid for classification problems) until then:

       

       

  • Comparisons to related work

    • Computationally, it is highly efficient: the operation of the self-attentional layer can be parallelized across all edges, and the computation of output features can be parallelized across all nodes.
    • As opposed to GCNs, our model allows for (implicitly) assigning different importances to nodes of a same neighborhood, enabling a leap in model capacity. Furthermore, analyzing the learned attentional weights may lead to benefits in interpretability.
    • The attention mechanism is applied in a shared manner to all edges in the graph, and therefore it does not depend on upfront access to the global graph structure or (features of) all of its nodes (a limitation of many prior techniques).
      • The graph is not required to be undirected.
      • It makes our technique directly applicable to inductive learning.
    • GraphSAGE samples a fixed-size neighborhood of each node, in order to keep its computational footprint consistent; this does not allow it access to the entirety of the neighborhood while performing inference.
    • In comparison to previ- ously considered MoNet instances, our model uses node features for similarity computations, rather than the node’s structural properties (which would assume knowing the graph structure upfront).

  • Datasets

    

  • Experimental setup

    • Transductive learning
      • Two-layer GAT model.
      • The first layer consists of K = 8 attention heads computing F ′ = 8 features each (for a total of 64 features), followed by an exponential linear unit (ELU) nonlinearity.
      • The second layer is used for classification: a single attention head that computes C features (where C is the number of classes), followed by a softmax activation.
      • L2 regularization with λ = 0.0005.
      • Dropout with p = 0.6 is applied to both layers’ inputs, as well as to the normalized attention coefficients (critically, this means that at each training iteration, each node is exposed to a stochastically sampled neighborhood).
    • Inductive learning
      • Three-layer GAT model.
      • Both of the first two layers consist of K = 4 attention heads computing F ′ = 256 features (for a total of 1024 features), followed by an ELU nonlinearity.
      • The final layer is used for (multi-label) classification: K = 6 attention heads computing 121 features each, that are averaged and followed by a logistic sigmoid activation.
      • No need to apply L2 regularization or dropout.
      • Employed skip connections across the intermediate attentional layer.

    Both models are initialized using Glorot initialization and trained to minimize cross-entropy on the training nodes using the Adam SGD optimizer with an initial learning rate of 0.01 for Pubmed, and 0.005 for all other datasets. In both cases we use an early stopping strategy on both the cross-entropy loss and accuracy (transductive) or micro-F1(inductive) score on the validation nodes, with a patience of 100 epochs .

  • Results

    

    

  • Interestring research direction

    Taking advantage of the attention mechanism to perform a thorough analysis on the model interpretability.

• EXISTING PROBLEMS: Overcoming the practical problems described in subsection 2.2 to be able to handle larger batch sizes.

• IMPROVEMENT IDEAS: 1. Sampling nodes base on the sorted result of attention weights maybe better. 2. Extending the method to perform graph classification instead of node classification would also be relevant from the application perspective. 3. Extending the model to incorporate edge features (possibly indicating relationship among nodes) would allow us to tackle a larger variety of problems.