算法：理解单源最短路径——Dijkstra

单源最短路径

指一个顶点到其余各个顶点的最短距离，

算法思路分析

下面以下图为例分析，算法的步骤。

根据上面的单向图，将其转化为邻接矩阵如下所示

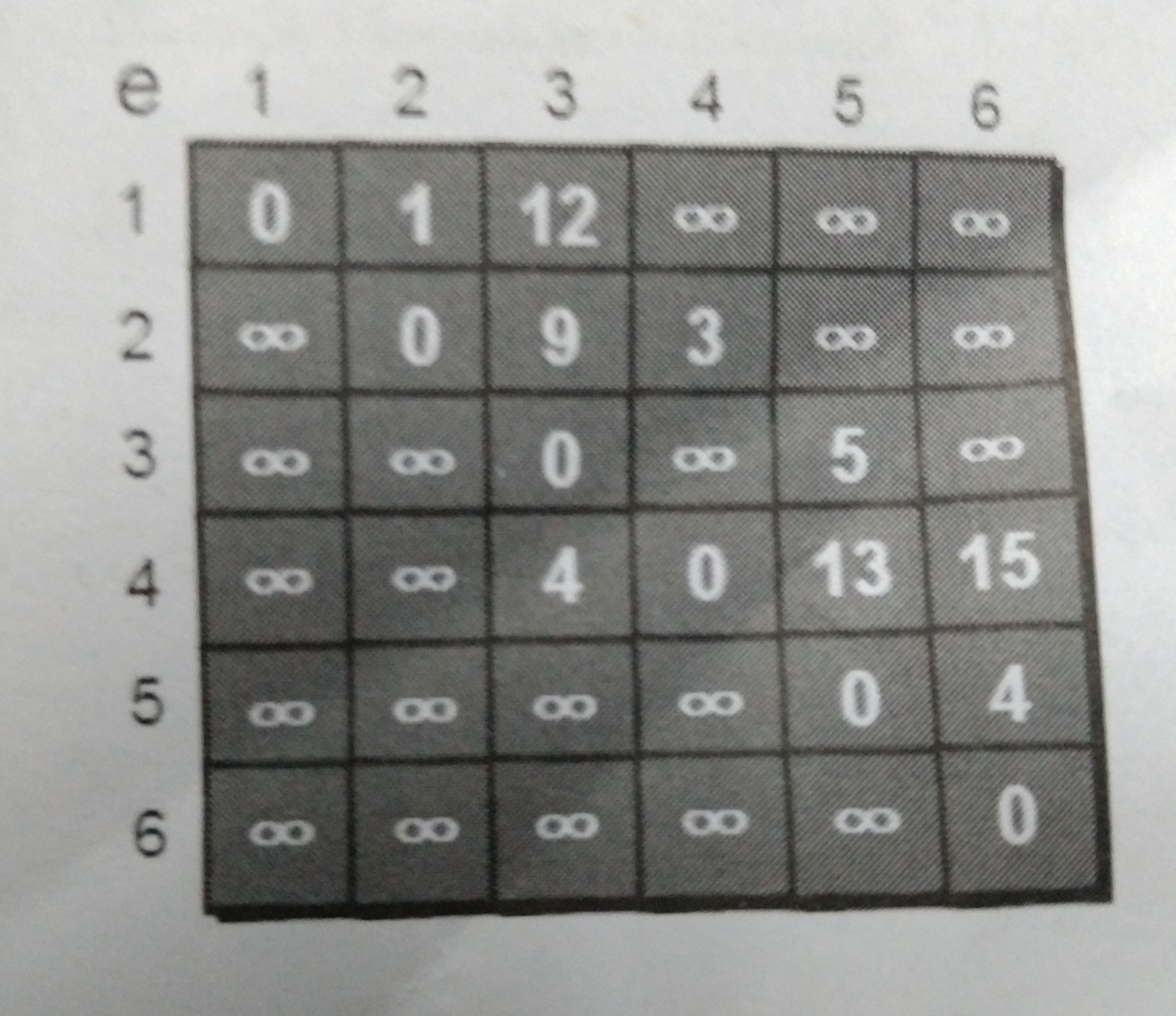
dijkstra算法基于贪心思想，要求单源点的最短路径，从未走过的边中取一条最短的。
将设要求源点1 到其他顶点的最短路径，用一个数组dis[6]来保存到各个顶点的距离,初始化为

dis[6]={0,1,12,1000,1000，1000}//1000表示极大

那么取一条最短的边[1]->[2]其距离为1，这条边就是1->2的最短距离，和floyd算法中通过中间点来找更短路径不同，因为1->2已经是最短的变了，通过中间点只会增加距离。

因此，dis[2]=1,就确定下来不需要再更新了，那么从1->2->2的临边，可以找到 1->2的临边（图中顶点3,4） 的更短路径，这里就需要做判断了。

比较dis[3] 和dis[2]+edge[2][3]，得到小者

更新完dis[3],dis[4]之后，

dis[6]={0,1,10,4,1000,1000}

以上过程叫做”松弛“，通过边松弛顶点1到其余个点的距离。

顶点2松弛过程完成之后，就可以再找顶点1的下一个最短的距离点了，那就是顶点4。

依次循环执行，直到顶点1到其他全部顶点的松弛过程都进行完。

最终结果

dis[6]={0,1,8,4,13,17}

这就是顶点1到其余各顶点的最短距离

算法归纳

1. 将顶点分为两部分，集合P和Q，P是每次取最短路径的顶点，最开始只有源点，Q是还没有作为最短路径顶点松弛的点。使用book[]数组来标记顶点是在P（book[]=1）还是Q。
2. 初始化源点到其他点的距离，dis[i]=graph[0][i]
3. 在集合Q中取一个距离源点1最近的顶点k将其book[]标记为1,通过k来获取源点到k的所有临点的更短路径
4. 重复3，直到集合Q为空，也就是book[]都为0了。

5. 算法实现

根据以上分析，java代码如下

package aha_algorithm;

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;

public class Dijkstra {

	static int[][] graph;
	static int book[];
	static int distance[];
	static int vertexNum, edgeNum;

	/**
	 * @param args
	 */
	public static void main(String[] args) {
		initGraph();
		dijkstra();
		for (int i = 0; i < distance.length; i++) {
			System.out.print(distance[i]+"  ");
		}
	}

	static void initGraph() {
		BufferedReader input = new BufferedReader(new InputStreamReader(System.in));

		try {
			String[] inLine = input.readLine().split(" ");

			vertexNum = Integer.valueOf(inLine[0]);
			edgeNum = Integer.valueOf(inLine[1]);

			graph = new int[vertexNum][vertexNum];
			book = new int[vertexNum];
			// 初始化矩阵
			for (int i = 0; i < vertexNum; i++) {
				for (int j = 0; j < vertexNum; j++) {
					if (i == j)
						graph[i][j] = 0;
					else
						graph[i][j] = 1000;
				}
			}
			// 获取边信息
			for (int i = 0; i < edgeNum; i++) {
				String[] edge = input.readLine().split(" ");
				graph[Integer.valueOf(edge[0])][Integer.valueOf(edge[1])] = Integer.valueOf(edge[2]);
			}

			// 初始化book
			for (int i = 0; i < vertexNum; i++) {
				book[i] = 0;
			}
			// 初始化distance，距离数组
			distance = new int[vertexNum];
			for (int i = 0; i < vertexNum; i++) {
				distance[i] = graph[0][i];
			}

			book[0]=1;//注意初始化源点
			
		} catch (IOException e) {
			e.printStackTrace();
		}

	}

	static void dijkstra() {
		for (int i = 0; i < vertexNum; i++) {// 遍历Q集合中所有顶点,这里的循环次数

			int minDistanceSource2J = Integer.MAX_VALUE;
			int minJ = 0 ;
			for (int j = 0; j < vertexNum; j++) {// 找到距离源点1的最短距离的顶点,查找算法
				if (book[j] == 0 && distance[j] < minDistanceSource2J) {
					minDistanceSource2J = distance[j];
					minJ = j;
				}
			}
			
			book[minJ]=1;
			
			//更新minJ的相邻点到原点的最短距离
			for (int j = 0; j <vertexNum ; j++) {
				if(graph[minJ][j]<1000){
					if(distance[j] > distance[minJ]+graph[minJ][j]){
						distance[j] = distance[minJ]+graph[minJ][j];
					}
				}
			}
			
		}
	}
	
	static void printGraph() {
		for (int i = 0; i < vertexNum; i++) {
			for (int j = 0; j < vertexNum; j++) {
				System.out.print(graph[i][j] + " ");
			}
			System.out.println();
		}
	}
	
}

用例和结果

输入：
6 9
0 1 1
0 2 12
1 2 9
1 3 3
2 4 5
3 2 4
3 4 13
3 5 15
4 5 4
结果：
0  1  8  4  13  17  

复杂度分析

基于邻接矩阵的时间复杂为O(n^2)

基于邻接表的稀疏矩阵复杂度为（M+N）logN.

使用堆可以优化查找源点到最短距离顶点的时间。即步骤3

dijkstra算法不能用于有负权边的图，因为有负权边就会修改已经在book中的顶点的最短距离，使得结果不正确。

该算法在判断是否要更新distance数组时与floyd算法做法类似，可以参考多源最短路径–floyd算法