【强化学习实战-06】Policy based RL保姆级教程：以Cart Pole为例

作者：刘兴禄，清华大学博士在读

本笔记整理自 (作者: Shusen Wang):
https://www.bilibili.com/video/BV1rv41167yx?from=search&seid=18272266068137655483&spm_id_from=333.337.0.0

强化学习的Policy based RL和Value based RL

强化学习中的两大类Policy based RL和Value based RL，分别是学习(或者)近似不同的函数。但是最终目的都是能够指导agent做动作。

要指导agent做动作，有下面两种方法：

1. 能够知道在状态s下，做每个动作a的期望总价值，就可以根据价值，做价值最大的动作。用数学的语言表达，就是学习动作-价值函数$Q(s,a)$，得到最优动作价值函数$$Q^{\ast }(s,a)$$，然后我们根据下面的表达式做动作即可。给定状态$s_t$，下一时刻的动作可以按照下面的标准选出：$$a_{t+1}=\text{arg}\underset{a\in \mathcal{A}}{\max }{Q}^{\ast }(s_t,a)$$。
2. 能够知道在状态s下，下一步做每个动作a的概率，就可以根据概率进行随机抽样，得到下一步的动作。用数学的语言表达，就是学习策略函数$\pi (a|s)$，得到最优策略函数$${\pi }^{\ast }(a|s)$$(也就是given 状态$s$，下一步做出动作$a$的最好的概率分布)，然后我们根据下面的表达式做动作即可。给定状态$s_t$，下一时刻的动作可以按照下面的标准选出 (注意$A_{t+1}$是随机变量)：
   $$A_{t+1}\sim {\pi }^{\ast }(\cdot |s_t)$$。选择的方法就是随机抽样，也就是，下一步具体要做的动作$a_{t+1}$是按照下面的方法选出：
   $$a_{t+1}\leftarrow \text{random choice }[{\pi }^{\ast }(\cdot |s_t)]$$

其中，第一种叫做Value based RL，第二种叫做Policy based RL。具体来讲就是

1. Value based RL: 以$Q^{\ast }(s,a)$指导agent做动作，给定状态$s_t$，下一步的动作为$a_{t+1}=\text{arg}{\max }_{a\in \mathcal{A}}{Q}^{\ast }(s_t,a)$。
2. Policy based RL: 以${\pi }^{\ast }(a|s)$指导agent做动作，利用随机抽样获得下一步要做的动作。给定状态$s_t$，下一步的动作为$a_{t+1}\leftarrow \text{random choice }[{\pi }^{\ast }(\cdot |s_t)]$。

这两种算法分别是如何实现的呢？

1. Value based RL:

• 用神经网络$Q(s,a;\theta )$去近似最优动作价值函数$Q^{\ast }(s,a)$，用TD-learning, SARSA等算法去训练$Q(s,a;\theta )$。之前的推文已经介绍了DQN, Double DQN, Dueling Double DQN，都是这种类型。

2. Policy based RL:

• 用神经网络$\pi (a|s;\theta )$去近似最优策略函数${\pi }^{\ast }(a|s)$，这里训练有几种方法：
• (1). 用Policy Gradient算法去训练单个策略网络$\pi (a|s;\theta )$，价值可以用REINFORCE来近似，不用神经网络。
• (2). 用基本的Actor-Critic算法去同时训练策略网络$\pi (a|s;\theta )$和价值网络$Q(s,a;\mathbf{w})$，其中策略网络$\pi (a|s;\theta )$用Policy Gradient算法更新，价值网络$Q(s,a;\mathbf{w})$用TD-learning等算法更新。
• (3). 用改进后的Actor-Critic算法，也就是 Advantage Actor-Critic (A2C)，或者 Asynchronous Advantage Actor Critic (A3C) 去同时训练策略网络$\pi (a|s;\theta )$和价值网络$Q(s,a;\mathbf{w})$，其中策略网络$\pi (a|s;\theta )$用Policy Gradient算法更新，价值网络$Q(s,a;\mathbf{w})$的构建参照Dueling Network，引入Advantage function(stream)，然后用TD-learning等算法更新$Q(s,a;\mathbf{w})$。

Policy based RL

Policy based RL就是用神经网络$\pi (s,a;\theta )$去近似最优策略函数${\pi }^{\ast }(a|s)$。这里，$\pi (s,a;\theta )$也叫策略网络。

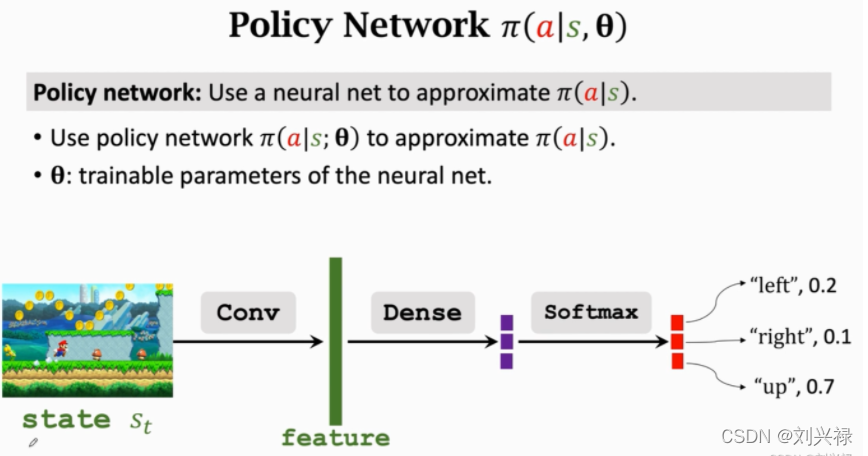
策略网络$\pi (s,a;\theta )$是一个概率分布，满足
$$\sum _{a\in \mathcal{A}}\pi (a|s;\theta )=1$$

价值函数：value function

首先我们需要再次回顾相关概念。

• 折扣回报(Discounted return): 也就是从$t$时刻到结束的累计总回报。$$\begin{array}{rl}{U}_t& =R_t+\gamma \cdot R_{t+1}+{\gamma }^2\cdot R_{t+2}+{\gamma }^3\cdot R_{t+3}+\cdots \\ & =\sum _{k=1}^{+\infty }{\gamma }^k{R}_{t+k}\end{array}$$

注意，大写字母都是随机变量。每一步的reward，也就是$R_t,R_{t+1},R_{t+2},\cdots$，全部是随机变量，因为我们并不知道真实、准确的reward function，只能是自己凭借经验去设置一个自己觉得合理的reward function。或者说，等待环境返回一个reward的观测值： $r_t$。

• 动作-价值函数（Action-value function）：$Q_{\pi }(s_t,a_t)$，表示在策略$\pi$下，状态为$s_t$时采取动作$a_t$，获得的总折扣回报$U_t$的期望。也就是$$Q_{\pi }(s_t,a_t)=\mathbb{E}[U_t|S_t=s_t,A_t=a_t]$$

另外，在Policy based reinforcement learning中，我们是学习状态价值函数$V_{\pi }(s)$，且$V_{\pi }(s)$等于
$$\begin{array}{rl}{V}_{\pi }(s_t)& ={\mathbb{E}}_A[Q_{\pi }(s_t,A)]\\ & =\sum _a\pi (a_t|s_t)\cdot Q_{\pi }(s_t,a_t)\approx \sum _a\pi (a_t|s_t;\theta )\cdot q(s_t,a_t;\mathbf{w})\end{array}$$
最后，我们会同时得到:

• 策略网络(policy network),也就是 Actor $\pi (a|s;\theta )$，和
• 价值网络(value network),也就是Critic $q(s,a;\mathbf{w})$。注意这个价值网络$q(s,a;\mathbf{w})$是不依赖于策略$\pi$的，因为它就是一个唯一的神经网络而已，$\pi$变化，神经网络$q(s,a;\mathbf{w})$不会变化。

虽然最后会同时得到策略网络(policy network)$\pi (a|s;\theta )$和价值网络(value network)$q(s,a;\mathbf{w})$，但是最后我们只是用策略网络(policy network)$\pi (a|s;\theta )$去做动作(相当于去求解问题)。

因此，我们引出状态-价值函数$V_{\pi }(s_t)$

• 状态-价值函数（State-value function）：$V_{\pi }(s_t)$，表示在策略$\pi$下，状态为$s_t$时会获得的总折扣回报$U_t$的期望。也就是
  $$\begin{array}{rl}{V}_{\pi }(s_t)& ={\mathbb{E}}_A[Q_{\pi }(s_t,A)]\\ & ={\mathbb{E}}_{a\sim \pi (s_t)}[Q_{\pi }(s_t,a)]\\ & =\sum _a\pi (a_t|s_t)\cdot Q_{\pi }(s_t,a_t)\end{array}$$

基于价值函数，我们因此最优价值函数的概念。

• 最优动作-价值函数（Optimal action-value function）：$Q^{\ast }(s,a)$，表示在所有可能的策略$\pi$下，状态为$s_t$时采取动作$a_t$，获得的总折扣回报$U_t$的期望的最大值。也就是$$Q^{\ast }(s_t,a_t)=\underset{\pi }{\max }{Q}_{\pi }(s,a)$$
  最优动作-价值函数（Optimal action-value function）可以直接指导Agent做动作。

• 最优状态-价值函数（Optimal state-value function）：$V^{\ast }(s)$，表示在所有可能的策略$\pi$下，状态为$s_t$时会获得的总折扣回报$U_t$的期望的最大值。也就是$$V^{\ast }(s)=\underset{\pi }{\max }{V}_{\pi }(s)$$
  最优状态-价值函数（Optimal state-value function）不可以直接指导Agent做动作，但是伴随其训练出的策略网络$\pi (a|s)$可以指导Agent做动作。

Policy based RL: 详细理论介绍

上面已经介绍到，将动作价值函数$Q_{\pi }(s,A)$中的动作$A$用积分消掉，就变成了状态价值函数，也就是
$$\begin{array}{rl}{V}_{\pi }(s_t)& ={\mathbb{E}}_A[Q_{\pi }(s_t,A)]\\ & ={\mathbb{E}}_{a\sim \pi (s_t)}[Q_{\pi }(s_t,a)]\\ & =\sum _{a\in \mathcal{A}}\pi (a_t|s_t)\cdot Q_{\pi }(s_t,a_t)\end{array}$$
比如，$s_t=\text{current frame}$，下一步动作的策略为$\pi (a|s_t=\text{left})=[\text{left=}0.1,\text{right=}0.2,\text{up=}0.7]$
则此时$V(s_t=\text{current frame})$的计算如下
$$\begin{array}{r}V(s_t=\text{current frame})=0.1\cdot Q(s_t,\text{left})+0.2\cdot Q(s_t,\text{right})+0.7\cdot Q(s_t,\text{up})\end{array}$$

• 这里：$V_{\pi }(s_t)$，给定策略$\pi$，如果$V_{\pi }(s_t)$小，说明策略函数$\pi$不好，胜算小。反之，如果$V_{\pi }(s_t)$大，说明策略函数$\pi$非常好，胜算大。我们就是要追求使得$V_{\pi }(s_t)$大的策略函数$\pi$。

我们可以看到，由于$V_{\pi }(s_t)$可以等价的写成$V_{\pi }(s_t)={\sum }_a\pi (a_t|s_t)\cdot Q_{\pi }(s_t,a_t)$，这个里面就正好包含了策略函数$\pi (a_t|s_t)$。那么，如果我们能直接近似得到$\pi (a_t|s_t)$，那就可以控制agent做动作了。那么如何做呢？

可以这么做：

1. 用一个神经网络$\pi (a|s_t;\theta )$去近似策略函数$\pi (a|s_t)$
2. 然后，这个神经网络可以辅助我们进一步去近似状态价值函数$V(s_t)$，也就是状态价值函数$V(s_t)$也可以用同一个神经网络近似，表示为$V(s_t;\theta )$ （注意$V(s_t;\theta )$和$\pi (a|s_t;\theta )$中的$\theta$指的是同一个神经网络。）
   $$V(s_t;\theta )=\sum _{a\in \mathcal{A}}\pi (a_t|s_t;\theta )\cdot Q_{\pi }(s_t,a_t)$$

这样，我们就用一个神经网络$\theta$，用$V(s_t;\theta )$来近似出了状态价值函数$V(s_t)$。同时，我们也可以得到策略网络$\pi (a|s_t;\theta )$，只需要基于策略网络$\pi (a|s_t;\theta )$指导agent做动作即可。

这里需要注意逻辑：由于$V_{\pi }(s_t)$本身是没办法指导agent做动作的。因此只得到$V_{\pi }(s_t)$还不够。我们需要将$V_{\pi }(s_t)$展开，也就是展开称为$V_{\pi }(s_t)={\sum }_a\pi (a_t|s_t)\cdot Q_{\pi }(s_t,a_t)$，我们通过用策略网络$\pi (a|s_t;\theta )$去近似$\pi (a|s_t)$，从而反推，近似出来$V_{\pi }(s_t)$，而$V_{\pi }(s_t)$是越大越好，我们就可以最后通过训练得到最好的$V_{\pi }(s_t)$，从而可以同时得到$V_{\pi }(s_t;\theta )$和$\pi (a|s_t;\theta )$，最后用$\pi (a|s_t;\theta )$指导agent做动作即可。整个过程价值网络$V_{\pi }(s_t;\theta )$只是为了给策略网络$\pi (a|s_t;\theta )$提供改进的方向，否则$\pi (a|s_t;\theta )$自己是无法得知改进方向的。

基于此，我们的目标，就是使得价值网络$V_{\pi }(s_t;\theta )$最大，也就是
$$\max V_{\pi }(s_t;\theta )\to \max \sum _{a\in \mathcal{A}}\pi (a_t|s_t;\theta )\cdot Q_{\pi }(s_t,a_t)$$

如何达到上面的目标呢，这就需要今天要讲的，策略梯度算法 (Policy Gradient)。

Policy Gradient 算法介绍

先说一个注意事项：
It is quite tricky to derive the policy gradient equation.，也就是要推导策略梯度方程是相当棘手的。

Policy Gradient的目的，就是要最大化状态价值函数。也就是要实现
$$\max V_{\pi }(s_t;\theta )\text{or }\max \sum _{a\in \mathcal{A}}\pi (a_t|s_t;\theta )\cdot Q_{\pi }(s_t,a_t)$$
由于我们实际上是用policy network $\pi (a_t|s_t;\theta )$自下而上的构造出$V_{\pi }(s_t;\theta )$去近似状态价值函数$V_{\pi }(s_t)$。因此，其实参数就只有policy network $\pi (a_t|s_t;\theta )$中的$\theta$，因此我们科技将其定义为$J(\theta )$。且
$$J(\theta )={\mathbb{E}}_S[V(S;\theta )]$$
我们对$S$进行积分，将$S$消掉。因此，我们的目标其实就是最大化$J(\theta )$，也就是
$$\max J(\theta )$$
也就是我们要学习最好的$\theta$使其最大化$J(\theta )$。

我们采用的方法就是Policy Gradient。

Policy Gradient的方法就是：在观测到状态$s$的时候，我们求出目标函数$V(s;\theta )$的梯度，然后用梯度上升去更新$\theta$使其最大化$V(s;\theta )$。

参考文献

• Sutton R S, McAllester D, Singh S, et al. Policy gradient methods for reinforcement learning with function approximation[J]. Advances in neural information processing systems, 1999, 12.

策略梯度Policy Gradient的关键是，如何求出策略梯度$$\frac{\partial V(s;\theta )}{\partial \theta }$$

如何求出策略梯度呢？下面我们来推导策略梯度Policy Gradient的形式。

Policy Gradient 的推导

我们开始推导
$$\begin{array}{rl}\frac{\partial V(s;\theta )}{\partial \theta }& =\frac{\partial {\sum }_{a\in \mathcal{A}}\pi (a_t|s_t;\theta )\cdot Q_{\pi }(s_t,a_t)}{\partial \theta }\text{和的导数等于导数的和，可以将偏导移进去}\\ & =\frac{{\sum }_{a\in \mathcal{A}}\partial \pi (a_t|s_t;\theta )\cdot Q_{\pi }(s_t,a_t)}{\partial \theta }\\ & =\sum _{a\in \mathcal{A}}\frac{\partial \pi (a_t|s_t;\theta )\cdot Q_{\pi }(s_t,a_t)}{\partial \theta }\text{这里暂时假设}Q(s_t,a_t)\text{与}\theta \text{无关，是一种简化}\\ & =\sum _{a\in \mathcal{A}}\frac{\partial \pi (a_t|s_t;\theta )}{\partial \theta }\cdot Q_{\pi }(s_t,a_t)\\ & =\sum _{a\in \mathcal{A}}\left[\pi (a_t|s_t;\theta )\cdot \frac{1}{\pi (a_t|s_t;\theta )}\right]\frac{\partial \pi (a_t|s_t;\theta )}{\partial \theta }\cdot Q_{\pi }(s_t,a_t)\text{等价转化}\\ & =\sum _{a\in \mathcal{A}}\pi (a_t|s_t;\theta )\cdot \left[\frac{1}{\pi (a_t|s_t;\theta )}\frac{\partial \pi (a_t|s_t;\theta )}{\partial \theta }\right]\cdot Q_{\pi }(s_t,a_t)\\ & =\sum _{a\in \mathcal{A}}\pi (a_t|s_t;\theta )\cdot \frac{\partial \log \pi (a_t|s_t;\theta )}{\partial \theta }\cdot Q_{\pi }(s_t,a_t)\\ & ={\mathbb{E}}_A\left[\frac{\partial \log \pi (A|s_t;\theta )}{\partial \theta }\cdot Q_{\pi }(s_t,A)\right]\pi (a_t|s_t;\theta )\text{是概率分布}\end{array}$$

最终我们有

$$\begin{array}{r}\frac{\partial V(s;\theta )}{\partial \theta }={\mathbb{E}}_A\left[\frac{\partial \log \pi (A|s_t;\theta )}{\partial \theta }\cdot Q_{\pi }(s_t,A)\right]\end{array}$$

下面的图片也是同样的推导过程。

根据上述推导，我们有

$$\begin{array}{r}\frac{\partial V(s;\theta )}{\partial \theta }={\mathbb{E}}_A\left[\frac{\partial \log \pi (A|s_t;\theta )}{\partial \theta }\cdot Q_{\pi }(s_t,A)\right]\end{array}$$

因此，策略梯度的形式有下面两种：

1. 第1种：对每个动作a求和的形式：$$\begin{array}{r}\frac{\partial V(s;\theta )}{\partial \theta }=\sum _{a\in \mathcal{A}}\frac{\partial \pi (a|s;\theta )}{\partial \theta }\cdot Q_{\pi }(s,a)\end{array}$$
   这种形式适用于离散动作的情况，因为得对所有动作$a$都求导然后加和。
2. 第2种：$$\begin{array}{r}\frac{\partial V(s;\theta )}{\partial \theta }={\mathbb{E}}_{A\sim \pi (\cdot |s;\theta )}\left[\frac{\partial \log \pi (A|s;\theta )}{\partial \theta }\cdot Q_{\pi }(s,A)\right]\end{array}$$
   这种形式比较常用，比较适用于连续动作(当然离散动作也可以用)，因为这是一个期望的形式，我们可以用蒙特卡洛近似的形式，按照策略函数$A\sim \pi (\cdot |s;\theta )$进行随机抽样，取一个动作$a$作为样本，去用随机梯度去代替期望。一个样本也是期望的无偏估计。

Policy Gradient 的具体计算

Policy Gradient的计算是基于上面介绍的两种梯度形式的。

分为离散动作和连续动作。

Policy Gradient 的计算: 离散动作

离散动作下，可以使用连加公式
$$\begin{array}{r}\frac{\partial V(s;\theta )}{\partial \theta }=\sum _{a\in \mathcal{A}}\frac{\partial \pi (a|s;\theta )}{\partial \theta }\cdot Q_{\pi }(s,a)\end{array}$$
计算策略梯度。

我们以超级马里奥为例子，假设可做的动作为[left, right, up]， 即$\mathcal{A}=$[left, right, up]。我们按照下面的方式计算策略梯度

• 令在动作$a$时的梯度的分量为$\mathbf{f}(a,\theta )$，即
  $$\begin{array}{r}\mathbf{f}(a,\theta )=\frac{\partial \pi (a|s;\theta )}{\partial \theta }\cdot Q_{\pi }(s,a)\end{array}$$
  则有(注意，这里我们其实是假设$Q_{\pi }(s,a)$是已知的，但是实际上他是未知的)
  $$\begin{array}{r}\frac{\partial V(s;\theta )}{\partial \theta }=\sum _{a\in \mathcal{A}}\mathbf{f}(a,\theta )\end{array}$$

1. 第一步：我们对每个动作$a\in \mathcal{A}$，都计算$\mathbf{f}(a,\theta )$；这里，其实就是对每个动作a，都计算$\frac{\partial \pi (a|s;\theta )}{\partial \theta }\cdot Q_{\pi }(s,a)$
2. 第二步：我们将所有$\mathbf{f}(a,\theta )$求和，得到$\frac{\partial V(s;\theta )}{\partial \theta }$，也就是
   $$\begin{array}{rl}\frac{\partial V(s;\theta )}{\partial \theta }& =\sum _{a\in \mathcal{A}}\mathbf{f}(a,\theta )\\ & =\mathbf{f}(\text{left},\theta )+\mathbf{f}(\text{right},\theta )+\mathbf{f}(\text{up},\theta )\end{array}$$

但是这里是需要注意的，上述的梯度计算，基于Pytorch的自动求导更新可能是不适用的，因为Pytorch可以调用函数loss.backward()实现自动的梯度下降更新，所以调用Pytorch实现这个的时候只需要定义好loss function就可以，然后让loss.backward()去自动地更新参数。需要注意下面几点。

1. 注意是梯度上升，因此loss需要做成负的，加一个负号。也就是，我们的目标本来是$$\max J(\theta )=\max V_{\pi }(s_t;\theta )$$，但是pytorch里面默认是$$\min \text{loss function}$$，为了实现梯度上升，我们需要将loss function其改成$$\min -J(\theta )=\min -V_{\pi }(s_t;\theta )$$
2. loss function其实就是目标函数，因此，在pytorch中，我们需要将loss function设置成为
   $$\text{loss}=-J(\theta )=-V_{\pi }(s_t;\theta )=-\sum _{a\in \mathcal{A}}\pi (a_t|s_t;\theta )\cdot Q_{\pi }(s_t,a_t)$$

Policy Gradient 的计算: 连续动作

上节介绍的梯度计算方法只适用于离散动作空间。对于连续动作空间，上述计算方法不再适用。

本节就来介绍连续动作空间下如何计算Policy Gradient。

之前我们经过推导，得到策略梯度的形式2：
$$\begin{array}{r}\frac{\partial V(s;\theta )}{\partial \theta }={\mathbb{E}}_{A\sim \pi (\cdot |s;\theta )}\left[\frac{\partial \log \pi (A|s;\theta )}{\partial \theta }\cdot Q_{\pi }(s,A)\right]\end{array}$$

因为这是一个期望的形式，我们可以用蒙特卡洛近似的形式，按照策略函数$A\sim \pi (\cdot |s;\theta )$进行随机抽样，取一个动作$a$作为样本，去用随机梯度去代替期望。一个样本也是期望的无偏估计。

另外，需要注意，除了一个样本是无偏估计以外，一个随机抽样的均值，也是无偏估计。

首先，我们用$\mathbf{g}(a;\theta )$表示$\frac{\partial V(s;\theta )}{\partial \theta }$，也就是令
$$\begin{array}{r}\mathbf{g}(a;\theta )=\frac{\partial V(s;\theta )}{\partial \theta }\end{array}$$

因此，具体操作如下：

连续动作下的策略梯度 （离散动作下也适用）

1. 根据策略网络$\pi (\cdot |s;\theta )$ (这相当于一个概率密度函数)，随机抽样，得到一个action $\hat{a}$。（$\hat{a}$是随机变量$A$的一个观测值）
2. 计算$$\mathbf{g}(\hat{a};\theta )=\frac{\partial \log \pi (\hat{a}|s;\theta )}{\partial \theta }\cdot Q_{\pi }(s,\hat{a})$$
   这里，显然
   – ${\mathbb{E}}_A[\mathbf{g}(A;\theta )]=\frac{\partial V(s;\theta )}{\partial \theta }$
   – $\mathbf{g}(\hat{a};\theta )$是$\frac{\partial V(s;\theta )}{\partial \theta }$的一个无偏估计。
3. 用$\mathbf{g}(\hat{a};\theta )$取近似策略梯度$\frac{\partial V(s;\theta )}{\partial \theta }$。

这种形式比较常用，比较适用于连续动作(当然离散动作也可以用)，

同样地，在Pytorch中，如何来设置loss function呢？还是那个原则，就是看目标函数。由于，我们一定是对目标函数求导(目标函数其实就是loss)，因此我们反推
$$\begin{array}{rl}& \frac{\partial V(s;\theta )}{\partial \theta }\approx \mathbf{g}(\hat{a};\theta )=\frac{\partial \log \pi (\hat{a}|s;\theta )}{\partial \theta }\cdot Q_{\pi }(s,\hat{a})\\ & ⟹\\ & \frac{\partial V(s;\theta )}{\partial \theta }\approx \frac{\partial \log \pi (\hat{a}|s;\theta )}{\partial \theta }\cdot Q_{\pi }(s,\hat{a})\end{array}$$
我们两边同时将偏导数去掉，得到
$$\begin{array}{rl}& \frac{\partial V(s;\theta )}{\partial \theta }\approx \mathbf{g}(\hat{a};\theta )=\frac{\partial \log \pi (\hat{a}|s;\theta )}{\partial \theta }\cdot Q_{\pi }(s,\hat{a})\\ & ⟹\\ & V(s;\theta )\approx \left[\log \pi (\hat{a}|s;\theta )\right]\cdot Q_{\pi }(s,\hat{a})\end{array}$$
再次强调，这里其实就是对状态-价值函数做了一个蒙特卡洛近似。可以理解为：$\left[\log \pi (\hat{a}|s;\theta )\right]\cdot Q_{\pi }(s,\hat{a})$是$V(s;\theta )$的无偏估计。用一个样本的值，去近似整体的期望。
因此，我们的目标函数就可以变化为
$$\begin{array}{r}\max V(s;\theta )\approx \max \left[\log \pi (\hat{a}|s;\theta )\right]\cdot Q_{\pi }(s,\hat{a})\end{array}$$
由于Pytorch默认梯度下降，而我们是要梯度上升，因此我们需要将目标函数变化为
$$\begin{array}{r}\min -V(s;\theta )\approx \min -\left[\log \pi (\hat{a}|s;\theta )\right]\cdot Q_{\pi }(s,\hat{a})\end{array}$$
因此，我们需要将loss function设置为
$$\begin{array}{rl}\text{loss function}& =-V(s;\theta )\\ & \approx -\left[\log \pi (\hat{a}|s;\theta )\right]\cdot Q_{\pi }(s,\hat{a})\end{array}$$
具体做法为：

1. 根据根据策略网络$\pi (\cdot |s;\theta )$，随机抽样，得到一个action $\hat{a}$；
2. 然后利用策略网络$\pi$计算出选择动作$\hat{a}$的概率$\pi (\hat{a}|s;\theta )$
3. 之后对$\pi (\hat{a}|s;\theta )$取对数，得到$\log \pi (\hat{a}|s;\theta )$；
4. 将对数动作概率$\log \pi (\hat{a}|s;\theta )$与动作价值$Q_{\pi }(s,\hat{a})$相乘，加一个负号，得到$-\left[\log \pi (\hat{a}|s;\theta )\right]\cdot Q_{\pi }(s,\hat{a})$。
   这样就完成了policy gradient下loss function的设置。

问题：$Q(s,a)$如何计算？

• 在上面的推导中，我们始终假设$Q(s,a)$已知。但是实际上，$Q(s,a)$我们是不知道的（如果$Q(s,a)$都提前知道了，直接就可以用$Q(s,a)$指导agent做动作了，还忙活搞策略网络$\pi (\hat{a}|s;\theta )$干啥，哈哈）。
• 下面我们将在算法迭代的介绍中，介绍如何计算$Q(s,a)$。

Policy Gradient: 算法迭代

这一部分来具体介绍Policy Gradient的算法迭代过程。

Policy Gradient: 算法迭代 （自己实现梯度下降的情况）

1. 观察到当前时刻的状态$s_t$；
2. 根据根据策略网络$\pi (\cdot |s;\theta )$，随机抽样，得到一个action $\widehat{a_t}$；
3. 计算动作价值$q_t\approx Q_{\pi }(s_t,\widehat{a_t})$，这里需要用一些估计的方法（更高级的算法中，使用神经网络去估计）。
4. 对策略网络求导（${\mathbf{d}}_{\theta ,t}$是第$t$时刻，loss function 对神经网络参数$\theta$的导数） $${\mathbf{d}}_{\theta ,t}=\frac{\partial \log \pi ({\hat{a}}_t|s_t;\theta )}{\partial \theta }{|}_{\theta ={\theta }_t}$$.
5. 计算策略梯度(实际上是估计策略梯度)，估计表达式为$$\mathbf{g}(\widehat{a_t};{\theta }_t)=q_t\cdot {\mathbf{d}}_{\theta ,t}$$
   其实，就是估计$\frac{\partial \log \pi (\hat{a}|s;\theta )}{\partial \theta }\cdot Q_{\pi }(s,\hat{a})$
6. 用梯度上升更新策略网络：
   $${\theta }_{t+1}\leftarrow {\theta }_t+\beta \cdot \mathbf{g}(\widehat{a_t};{\theta }_t)$$.

上面的过程，是自己写梯度下降，做反向传播的过程。

如果说我们调用pytorch来实现的话，步骤会简单一些，因为调用loss.backward()函数，神经网络会自动完成反向传播。因此，过程变化为

Policy Gradient: 算法迭代 （调用Pytorch的情形）

1. 观察到当前时刻的状态$s_t$；
2. 根据根据策略网络$\pi (\cdot |s;\theta )$，随机抽样，得到一个action $\widehat{a_t}$；（$\hat{a}$是随机变量$A$的一个观测值）
3. 计算动作价值$q_t\approx Q_{\pi }(s_t,\widehat{a_t})$，这里需要用一些估计的方法（更高级的算法中，使用神经网络去估计）。
4. 利用策略网络$\pi$计算出选择动作$\hat{a}$的概率$\pi (\hat{a}|s;\theta )$，之后对$\pi (\hat{a}|s;\theta )$取对数，得到$\log \pi (\hat{a}|s;\theta )$；
5. 设置策略网络的loss function为：
   $$\begin{array}{r}\text{loss function}=(\approx )-\left[\log \pi (\hat{a}|s;\theta )\right]\cdot q_t\end{array}$$
6. 用梯度下降更新策略网络（本来是梯度上升，但是由于我们将$\max obj$变成了$\min -obj$， 因此就可以是梯度下降了）：调用函数loss.backward()即可。

上面的迭代中，我们提到，我们需要有一个估计的方法，用$q_t$去估计动作价值$Q_{\pi }(s,\hat{a})$。那么$q_t$应该如何去计算呢？

可以用下图提到的方法。

我们来总结一下上面的方法。

方法1：REINFORCE

1. 我们让agent玩一局游戏，并且记录状态、动作、奖励的轨迹，也就是记录$$s_1,a_1,r_1,s_2,a_2,r_2,\cdots ,s_T,a_T,r_T.$$
   其中，$T$是最大的尝试次数，为了避免游戏一直结束不了。
2. 我们基于这个轨迹计算，对所有$t$，也就是$\forall t\in T$计算其折扣回报$$u_t=\sum _{k=t}^T{\gamma }^{k-t}{r}_k$$
3. 我们用$u_t$去近似$Q(s_t,a_t)$，也就是令$q_t=u_t$。这是因为$$Q_{\pi }(s_t,a_t)=\mathbb{E}[U_t]$$，因此，我们可以用随机变量$U_t$的一个实现值$u_t$去评估$Q(s_t,a_t)$，这也是无偏估计。

这也就是所谓的REINFORCE算法。

方法2：Actor-Critic算法

• 我们用一个神经网络$Q(s,a;\theta )$去近似动作价值函数$Q(s_t,a_t)$，这也就是所谓的Actor-Critic算法。

这个再下文中进行介绍。

Policy Gradient实战：求解Cart-Pole问题

搭建策略网络

策略网络$\pi (s,a;\theta )$是一个概率分布，满足
$$\sum _{a\in \mathcal{A}}\pi (a|s;\theta )=1$$

下面是我自己写的网络结构部分代码

'''
Author:     Liu Xinglu
Institute:  Tsinghua University
Email:      hsinglul@163.com
Date:       2022-02-28
'''

""" 策略梯度算法方差很大，设置seed以保证复现性 """

import gym
import torch
import torch.nn as nn
import numpy as np
from collections import deque
import random
from itertools import count
import torch.nn.functional as F
# from tensorboardX import SummaryWriter
from torch.utils.tensorboard import SummaryWriter
import math


""" 
This code is the basic implementation of the Policy Gradient algorithm 
"""
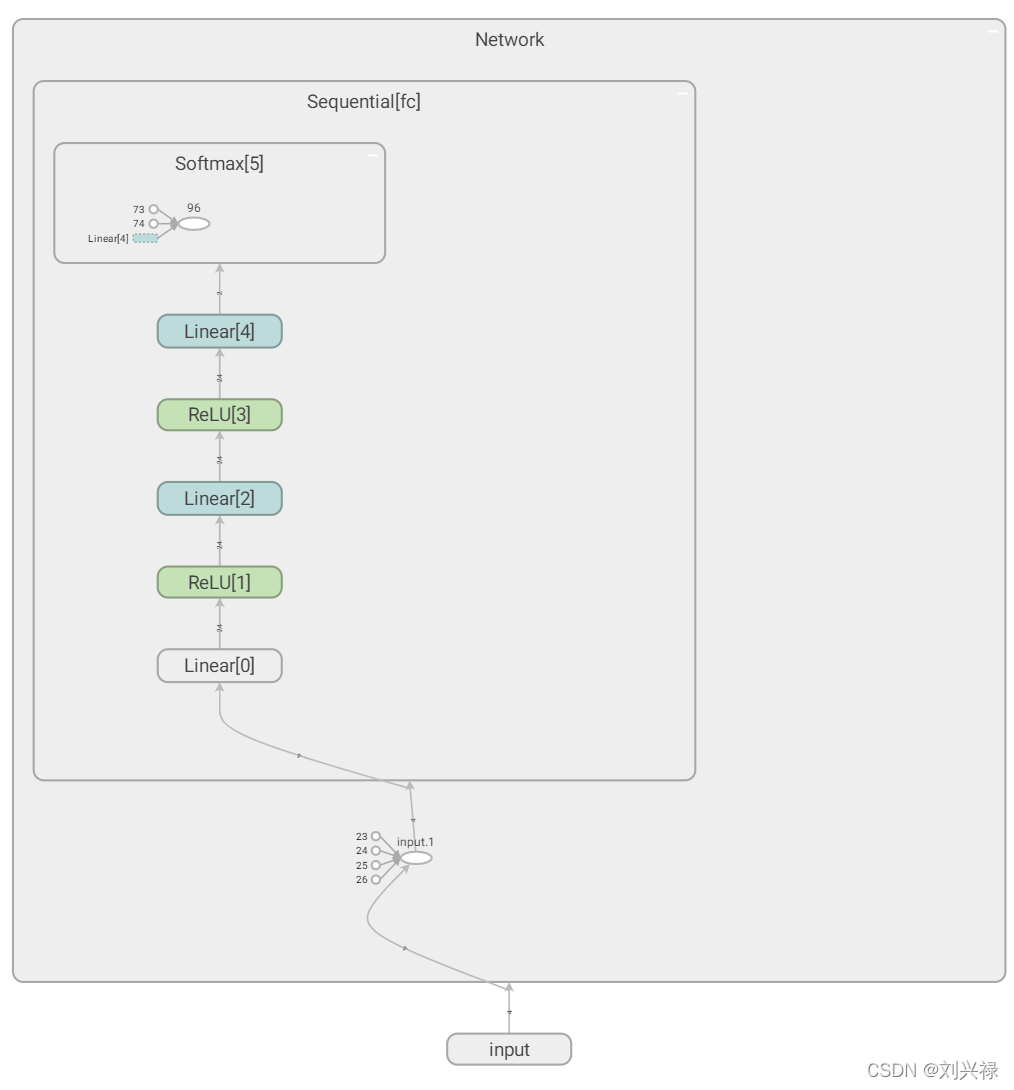
class Policy_Network(nn.Module):
    def __init__(self):
        super(Network, self).__init__()

        '''
         Input: state = (Cart Position, Cart Velocity, Pole Angle, Pole Angular Velocity )
         
         Output: probability of [left, right]
        '''
        self.fc = nn.Sequential(
            nn.Linear(4, 24),
            nn.ReLU(),
            nn.Linear(24, 24),
            nn.ReLU(),
            nn.Linear(24, 2),
            nn.Softmax(dim=-1)  # 按照输出向量的最后一个维度进行softmax，最后输出动作的概率
            # # 我们也可以在forward函数里面定义softmax
        )

        """ 
            the loss is actually the objective function of the neural network 
            In this problem, we pursue: 
                    the state value V(s; theta) is maximized 
                    where V(s; theta) = sum_{a} { pi (s|a; theta) * Q(s, a) }
                    这里我们训练的是 策略网络 pi (s|a; theta)， Q(s, a)我们用一些近似的方法去评估即可
                    
            Thus, the loss can be set to 
                loss = V(s; theta) 
                     = sum_{a} { pi (s|a; theta) * Q(s, a) } 
            
            目前还设置不了，等到真正用到的时候再去设置 
        """
        self.loss = None
        self.optimizer = torch.optim.Adam(self.parameters(), lr=0.001)

    def forward(self, state):
        return self.fc(torch.Tensor(state))

    # 如果在forward函数里面定义softmax，用下面的
    # def forward(self, state):
    #     output = self.fc(torch.Tensor(state))
    #     output = torch.softmax(output, dim=-1)   # 我们在forward函数里面定义softmax
    #
    #     return output

    def learn(self, state, reward, state_, gamma):
        '''
        Update policy network by TD learning.
            q_t = Q(s, a; theta): 是value network q(s,a; theta)的评估，是不太靠谱的
            q_target = r + gamma * q_t+1 : 这个由r的部分是真实的，所以我们认为他是相对靠谱的，我们将其作为标签

            我们的目的，就是让 q_t 尽量接近标签 q_target

            因此，目标函数是 min  1/2 * (q_t - q_target) ** 2
            也就是 loss function = 1/2 * (q_t - q_target) ** 2

        :param state: the current state
        :param reward: the immediate reward obtained from the environment
        :param state_: the new state after performing the action a
        :param gamma: the discount factor

        :return: TD_error: return TD_error, TD error后续会被用于更新 policy network
        '''
        q_target_next = 0
        with torch.no_grad():
            q_target_next = self.forward(torch.Tensor(state_)).detach()

        q_value = self.forward(torch.Tensor(state))   # 由于要对q_value求导，因此，这里不能用.detach()

        q_value_clone = self.forward(torch.Tensor(state)).detach() # 这个是用来计算TD_error，传给别人的，因此深拷贝

        q_target = reward + gamma * q_target_next  # 用Target_net来计算TD-target

        TD_error = q_target - q_value_clone

        loss = self.MSELoss(q_value, q_target)  # 计算loss
        self.optimizer.zero_grad()  # 将DQN上步的梯度清零
        loss.backward(retain_graph=True)  # DQN反向传播，更新参数
        self.optimizer.step()  # DQN更新参数

        return TD_error

    def random_choose_action(self, state):
        '''
        To select the next action under state s randomly under the PDF of policy.
        For Cart-Pole problem, the available actions are [left, right]

        :param state: the current state
        :return: int 类型, the selected next action ID
        '''
        action_ID = 0
        with torch.no_grad():
            """Example: the action_prob = tensor([0.5191, 0.5949]), we can randomly sample """
            softmax_action_probs = self.forward(torch.Tensor(state))

            """ np.random.choice([0, 1], size=1, p=softmax_action_probs)  表示在集合[0,1]中，以概率分布p随机抽取size的样本"""
            softmax_action_probs = softmax_action_probs.numpy().tolist()
            softmax_action_probs[0] = round(softmax_action_probs[0], 2)
            softmax_action_probs[1] = 1 - softmax_action_probs[0]
            action_ID = np.random.choice([0, 1], size=1, p=softmax_action_probs)[0]  # 注意，这个返回的是数组array([1])，我们只要int类型，因此加了[0]

        return action_ID


'''
# 这部分是为了较快可视化一下神经网络的结构
env = gym.envs.make('CartPole-v1')
env = env.unwrapped
policy_network = Network()   # policy_network, 需要训练的网络

writer = SummaryWriter("logs_policy_network_Cart_Pole")   # 注意tensorboard的部分

state = env.reset()  # 重置环境
writer.add_graph(model=policy_network, input_to_model=torch.Tensor(state))
writer.close()
'''

我们用tensorboard进行可视化

打开Pycharm的terminal，cd到log所在的目录logs_policy_network_Cart_Pole下，执行

tensorboard --logdir=logs_policy_network_Cart_Pole

这个是我在Network的构造函数_init_部分实现softmax的情况。

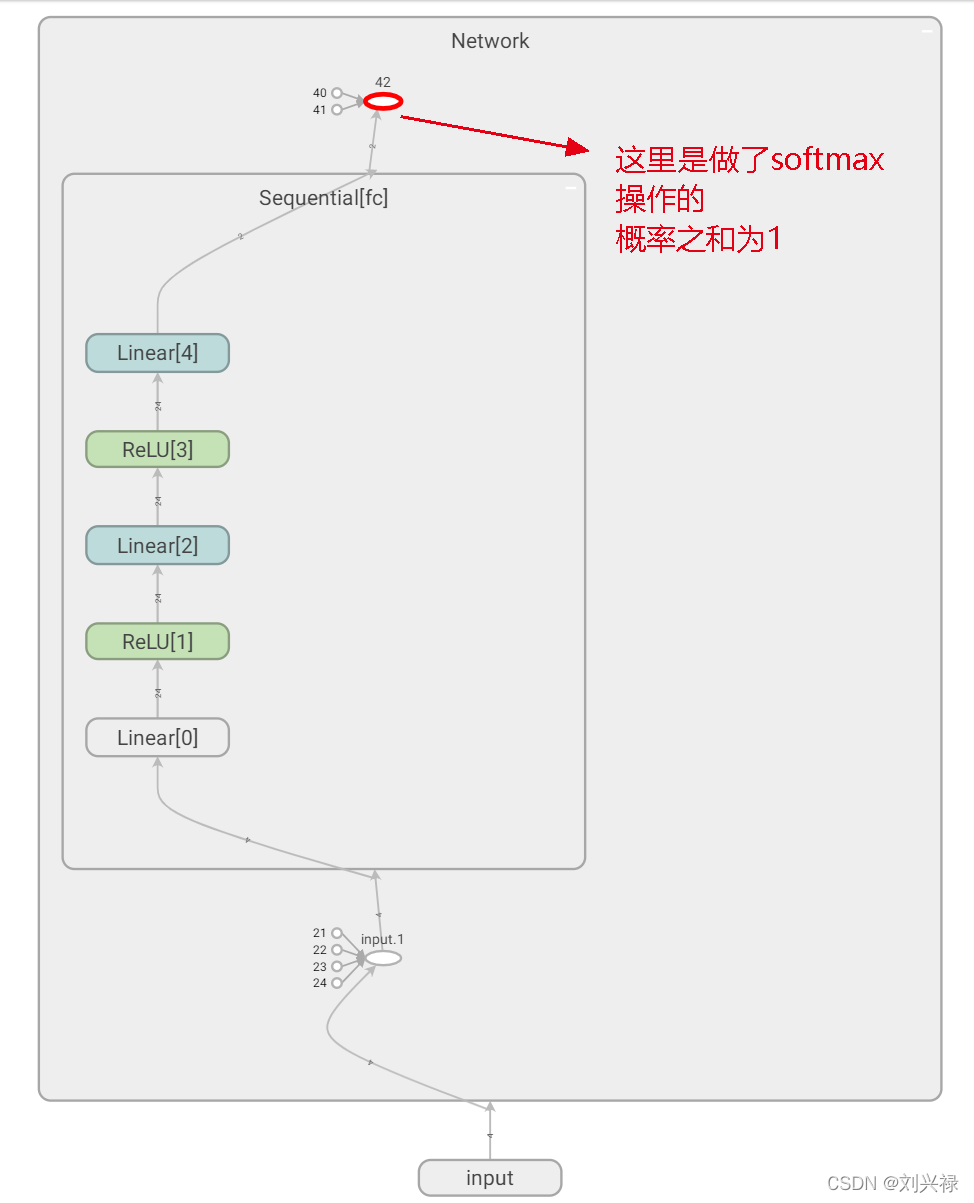
这个是我在forward部分实现softmax的情况。

Pytorch的Variable

Variable就是变量的意思。实质上也就是可以变化的量，区别于int变量，它是一种可以变化的变量，这正好就符合了反向传播，参数更新的属性。
pytorch都是由tensor计算的，而tensor里面的参数都是Variable的形式。如果用Variable计算的话，那返回的也是一个同类型的Variable。

注：tensor不能反向传播，variable可以反向传播。
Variable计算时，它会逐渐地生成计算图。这个图就是将所有的计算节点都连接起来，最后进行误差反向传递的时候，一次性将所有Variable里面的梯度都计算出来，而tensor就没有这个能力。

也就是说，如果想让一个量参与反向传播，可以用这个。

from torch.autograd import Variable

            # Gradient Desent
            optimizer.zero_grad()

            for i in range(steps):
                state = state_pool[i]
                action = Variable(torch.FloatTensor([action_pool[i]]))
                reward = reward_pool[i]

                probs = policy_net(state)
                m = Bernoulli(probs)
                loss = -m.log_prob(action) * reward  # Negtive score function x reward
                loss.backward()

            optimizer.step()

注意，也许神经网络中并没有包含action，但是我们的神经网络输出的是action的概率，我们要用这个去反向传播，结果action是一个tensor，可能神经网络识别不出来他是Variable，因此不能反向传播求导。

此时我们可以将其变为一个Variable，这样就可以了。

评估动作价值$q_t=Q_{\pi }(s,a)$

在前面的介绍中，我们提到，在Policy Gradient中，$q_t=Q_{\pi }(s,a)$并不是用神经网络评估的，而是用其他方法评估的。

一个参考代码：

https://towardsdatascience.com/breaking-down-richard-suttons-policy-gradient-9768602cb63b

参考代码4：实现了batch操作，比较不错的代码，我做了详细注释

这个代码来自

• https://github.com/Finspire13/pytorch-policy-gradient-example/blob/master/pg.py
• Policy Gradient 求解 Cart-Pole问题，实现了batch操作

"""
@ Author: Peter Xiao
@ Date: 2020/7/23
@ Filename: Actor_critic.py
@ Brief: 使用 Actor-Critic算法训练CartPole-v0
网址： https://github.com/Finspire13/pytorch-policy-gradient-example/blob/master/pg.py
"""

"""
    这个代码也是实现了policy gradient，并且是用batch来训练的
    代码结构和来自书的代码相似
    我在代码中加了大量的注释 

"""

import torch
import torch.nn as nn
import torch.nn.functional as F
from torch.distributions import Bernoulli
from torch.autograd import Variable
from itertools import count
import matplotlib.pyplot as plt
import numpy as np
import gym
import pdb


class PolicyNet(nn.Module):
    def __init__(self):
        super(PolicyNet, self).__init__()

        self.fc1 = nn.Linear(4, 24)
        self.fc2 = nn.Linear(24, 36)
        self.fc3 = nn.Linear(36, 1)  # Prob of Left
        """  这个代码值预测了向左的概率，而不是同时得到输出向左和向右的概率，也是可以的 """

    def forward(self, x):
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        # x = F.sigmoid(self.fc3(x))   # 注意 F.sigmoid(self.fc3(x)) 会报警告，但是不报错，是版本的问题
        x = torch.sigmoid(self.fc3(x))
        return x


def main():

    # Plot duration curve:
    # From http://pytorch.org/tutorials/intermediate/reinforcement_q_learning.html
    """
    这个函数是用来画图的，旨在将每一个episode的平均reward画出来
    :return:
    """
    episode_ID_set = []
    def plot_durations():
        plt.figure(2)
        plt.clf()
        durations_t = torch.FloatTensor(episode_ID)
        plt.title('Training...')
        plt.xlabel('Episode')
        plt.ylabel('Duration')
        plt.plot(durations_t.numpy())
        # Take 100 episode averages and plot them too
        if len(durations_t) >= 100:
            means = durations_t.unfold(0, 100, 1).mean(1).view(-1)
            means = torch.cat((torch.zeros(99), means))
            plt.plot(means.numpy())

        plt.pause(0.001)  # pause a bit so that plots are updated

    """
        设置学习 num_episode = 5000 个会合
        batch_size = 5， 每次学习5个episode的transitions
        之后的代码中，识别batch，是通过 设置 done = True时候的reward = 0 来识别已经记录的 episode 的个数的 
    """
    # Parameters
    num_episode = 5000
    batch_size = 5
    learning_rate = 0.01
    gamma = 0.99

    env = gym.make('CartPole-v0')
    policy_net = PolicyNet()
    optimizer = torch.optim.RMSprop(policy_net.parameters(), lr=learning_rate)

    """
        state_pool. action_pool, reward_pool
        都是用于在 reinforce 算法中收集 轨迹 trajectory 对应的 state. action, reward 的
        相邻 trajectory 之间，通过设置 reward = 0 来识别，具体方法见下面的注释
    """
    # Batch History
    state_pool = []
    action_pool = []  # 例如 actions = [0, 0, 0, 1, 0, 1, 0, 1, 1, 0, 0, 0, 1, 0, 1]   # 1*15个
    reward_pool = []  # 例如 rewards = [1.0, 1.0, 1.0, 1.0, 1.0, 0, 1.0, 1.0, 1.0, 1.0, 0, 1.0, 1.0, 1.0, 1.0] # 1*15个， 注意，两个0的位置是区分点，是为了区分不同的trajectory
    steps = 0    # 记录所有被记录的  trajectory 一共玩了多少步，其实就等于 reward_pool 的长度


    # 开始逐个 episode 学习
    for episode_ID in range(num_episode):

        state = env.reset()
        state = torch.from_numpy(state).float()
        state = Variable(state)
        # env.render(mode='rgb_array')
        env.render()

        for t in count():

            probs = policy_net(state)  # 得到向左的概率
            m = Bernoulli(probs)       # 根据概率构造分布
            action = m.sample()        # 根据分布随机抽样得到 action

            action = action.data.numpy().astype(int)[0]
            next_state, reward, done, _ = env.step(action)
            env.render()

            # To mark boundarys between episodes
            if done:
                reward = 0

            state_pool.append(state)
            action_pool.append(float(action))
            reward_pool.append(reward)

            state = next_state
            state = torch.from_numpy(state).float()
            state = Variable(state)

            steps += 1

            if done:
                episode_ID_set.append(t + 1)  # 这里是为了画图的
                plot_durations()              # 画图
                break

        # -----------在这上面，到 for episode_ID in range(num_episode): 其实就是玩了一局游戏，生成了一个  trajectory

        # Update policy
        if episode_ID > 0 and episode_ID % batch_size == 0:    # 这里，是为了每次收集 batch_size 个 trajectory 的数据

            """ 这里是利用收集好的 trajectory 的数据，计算 cumulative_discounted_return  """
            # Discount reward
            cumulative_discounted_return = 0
            for i in reversed(range(steps)):
                if reward_pool[i] == 0:
                    cumulative_discounted_return = 0
                else:
                    cumulative_discounted_return = cumulative_discounted_return * gamma + reward_pool[i]
                    reward_pool[i] = cumulative_discounted_return

            """ 这里跟那本书的代码一样，为了避免 cumulative_discounted_return 方差过大，做了标准化，减小训练数据方差 """
            # Normalize reward
            reward_mean = np.mean(reward_pool)
            reward_std = np.std(reward_pool)
            for i in range(steps):
                reward_pool[i] = (reward_pool[i] - reward_mean) / reward_std

            """ 下面就是计算 loss 并且进行 梯度下降了， 注意 loss 等于batch里面所有训练数据的单个样本的loss之和， 另外一个版本代码中也有解释"""
            # Gradient Desent
            optimizer.zero_grad()   # 在求导之前，先把上一步的梯度清零，否则会累加

            for i in range(steps):
                state = state_pool[i]
                action = Variable(torch.FloatTensor([action_pool[i]]))   # 这个是那一步采取的动作 (当时是随机采样得到的)
                cumulative_discounted_return = reward_pool[i]    # 这个就是评估的 q_t

                probs = policy_net(state)     #  得到概率的预测值
                m = Bernoulli(probs)          # 得到伯努利分布
                loss = -m.log_prob(action) * cumulative_discounted_return  # Negtive score function x reward   # 计算单个样本的 loss = - log(prob) * U_t
                loss.backward()     # 这里做 loss.backward() 也是可以的，因为如果梯度不清零，梯度是会自动累加的

            # loss.backward()       # 也可以在这里统一 loss.backward()
            optimizer.step()        # 梯度下降，更新参数

            state_pool = []         # 清空记忆库
            action_pool = []        # 清空记忆库
            reward_pool = []        # 清空记忆库
            steps = 0               # 清空本轮学习 过程中探索的步数 


if __name__ == '__main__':
    main()

参考代码5：教材中的代码

教材名称： 【Reinforcement Learning Cookbook Over 60 recipes to design, develop, and deploy self-learning AI models using Python】
页码： pp 262–265

强调： Reinforce算法其实就是一种batch操作。每一次reinforce，生成一个长度为T的轨迹trajectory （这个T是每一局游戏都不一样的，因为不确定多少步结束游戏），因此就相当于有T个transition，我们实际上是基于这T个transition去学习、更新网络。虽然是会合更新，但是其实也是一种batch操作。只不过batch size不固定而已。

'''
代码来自于教材：
> 教材名称： 【Reinforcement Learning Cookbook Over 60 recipes to design, develop, and deploy self-learning AI models using Python】
> 页码： pp 262--265
'''

import gym
import torch
import torch.nn as nn
env = gym.make('CartPole-v0')


class PolicyNetwork():
    # Let's start with the __init__method of the PolicyNetwork class, which
    # approximates the policy using a neural network:
    def __init__(self, n_state, n_action, n_hidden=50, lr=0.001):
        self.model = nn.Sequential(
            nn.Linear(n_state, n_hidden),
            nn.ReLU(),
            nn.Linear(n_hidden, n_action),
            # nn.Softmax(),   # 这个写法在早期的pytorch版本是没有警告的，现在因为其他考虑，要加上有指明dim参数。
            nn.Softmax(dim=-1),
        )
        self.optimizer = torch.optim.Adam(self.model.parameters(), lr)
        # 这个loss比较麻烦，就不在这里定义了，在后面会计算

    # Next, add the predict method, which computes the estimated policy
    def predict(self, s):
        """
        Compute the action probabilities of state s using the learning model
        @param s: input state
        @return: predicted policy，其实就是[left的概率， right的概率]
        """
        return self.model(torch.Tensor(s))

    # We now develop the training method, which updates the neural network with
    # samples collected in an episode:
    def update(self, returns, log_probs):
        """
        Update the weights of the policy network given the training samples
        @param returns: return (cumulative rewards) for each step in an episode
        @param log_probs: log probability for each step

		Note:
		--------
			return 是期望总价值的评估，是根据单步immediate reward计算的折扣回报
			Example：
				如果rewards = [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]  # 1 * 15，是一个做了15次的轨迹
				如果gamma = 0.9, 折扣回报计算结果为
				returns = tensor([7.9411, 7.7123, 7.4581, 7.1757, 6.8619, 	6.5132, 6.1258, 5.6953, 5.2170, 4.6856, 4.0951, 3.4390, 2.7100, 1.9000, 1.0000])
				log_probs: 是每一步执行动作的概率的log值，由于在Policy gradient中，reinforce我们是按照动作概率随机抽样
					比如probs=[0.6， 0.4]，我们抽样，得到action=0， reward=1,
					因此，我们actions.append(action); rewards.append(reward)
					并且，我们需要计算抽出的action对应的概率的log,也就是log(0.6)
					然后我们 log_probs.append(log(0.6))
					就是这样的操作
        """

        policy_gradient = []
        # 注意：这里policy_gradient是记录整个轨迹中所有transition下的分量loss，最后求和的
        # 比如：t=1, 第1个transition，loss_0 = -log_prob[0] * returns[0]
        # 比如：t=2, 第2个transition，loss_1 = -log_prob[1] * returns[1]
        # 最后求和：loss = loss_0 + loss_1 + ... + loss_T
        # 也就是下面的 loss = torch.stack(policy_gradient).sum()

        for log_prob, U_t in zip(log_probs, returns):
            policy_gradient.append(-log_prob * U_t)  # 求轨迹中单个transition的loss

        loss = torch.stack(policy_gradient).sum()   # 对轨迹中所有transition的loss求和，得到总loss

        self.optimizer.zero_grad()  # 在求导之前，先将前一步的导数清零，否则会叠加
        loss.backward()   # 反向传播求出参数的导数
        self.optimizer.step()  # 梯度下降更新神经网络参数

    # 5. The final method for the PolicyNetwork class is get_action, which samples
    # an action given a state based on the predicted policy:
    def get_action(self, s):
        """
        Estimate the policy and sample an action, compute its log probability
        @param s: input state
        @return: the selected action and log probability
        	例如：返回 action = 0， log_prob = log(0.6)
        """
        probs = self.predict(torch.Tensor(s))
        action = torch.multinomial(input=probs, num_samples=1).item()   #随机抽样 其中probs就是抽样的权重
        # torch.multinomial(probs, 1).item() 是随机抽样，probs是权重，1是抽样的个数
        log_prob = torch.log(probs[action])  #如果 action = 0, 则 torch.log(probs[action]) torch.log(probs[0]) = log (向左的概率)

        return action, log_prob

    # It also returns the log probability of the selected action, which will be used as part of the training sample


# Now, we can move on to developing the REINFORCE algorithm with a policy network model:
def reinforce(env, policy_net, n_episode, gamma=1.0):
    """
    REINFORCE algorithm
    @param env: Gym environment
    @param estimator: policy network
    @param n_episode: number of episodes
    @param gamma: the discount factor
    """
    for episode in range(n_episode):
        log_probs = []  # 必须要，计算loss以及梯度下降用得到
        rewards = []    # 必须要，计算折扣回报returns以及梯度下降用得到
        actions = []    # 可删去，放在这里是为了debug方便
        states = []     # 可删去，放在这里是为了debug方便
        state = env.reset()
        states.append(state)   # 可删去，放在这里是为了debug方便
        while True:
            action, log_prob = policy_net.get_action(state)
            next_state, reward, is_done, _ = env.step(action)
            # if(is_done == True):
            #     print('DONE')    # 这个是为了调试用的，看一个episode
            total_reward_episode[episode] += reward  # total_reward_episode里面一个元素代表一个轨迹的总reward，主要是用来看看目前模型效果如何了

            log_probs.append(log_prob)  # 例如 log_probs = [-0.5651,-0.5807,-0.5959,-0.8173,-0.5932,-0.8210,-0.5895,-0.8286,-0.8165,-0.5679,-0.5757,-0.5504,-0.9293,-0.5300,-0.9650]
            rewards.append(reward)  # 例如rewards = [1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0] # 1*15个
            actions.append(action)  # 例如actions = [0, 0, 0, 1, 0, 1, 0, 1, 1, 0, 0, 0, 1, 0, 1]   # 1*15个

            """
                is_done == True
                这说明一个episode结束了，我们记录了一个轨迹的信息，接下来就是REINFORCE来计算评估的 u_t了
                这种方法是用一个轨迹去估计，这是一个无偏估计，是蒙特卡洛近似
                
                这里，其实只需要整个轨迹的reward，以及相应的 log_probs即可。例如
                rewards = [1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0] # 1*15个 
                log_probs = [tensor(-0.5651, grad_fn=<LogBackward>),
                             tensor(-0.5807, grad_fn=<LogBackward>),
                             tensor(-0.5959, grad_fn=<LogBackward>),
                             tensor(-0.8173, grad_fn=<LogBackward>),
                             tensor(-0.5932, grad_fn=<LogBackward>),
                             tensor(-0.8210, grad_fn=<LogBackward>),
                             tensor(-0.5895, grad_fn=<LogBackward>),
                             tensor(-0.8286, grad_fn=<LogBackward>),
                             tensor(-0.8165, grad_fn=<LogBackward>),
                             tensor(-0.5679, grad_fn=<LogBackward>),
                             tensor(-0.5757, grad_fn=<LogBackward>),
                             tensor(-0.5504, grad_fn=<LogBackward>),
                             tensor(-0.9293, grad_fn=<LogBackward>),
                             tensor(-0.5300, grad_fn=<LogBackward>),
                             tensor(-0.9650, grad_fn=<LogBackward>)]    # 1*15个 
            """
            if is_done:   # 这说明一个episode结束了
                returns = []
                U_t = 0
                gamma_pow = 0
                for reward in rewards[::-1]:   # 就是从后往前循环，计算u_T, u_{T-1}, ...., u_1
                    U_t += gamma ** gamma_pow * reward    # U_t = sum (gamma_pow * reward_t), 也就是我的笔记中的公式
                    gamma_pow += 1
                    returns.append(U_t)  # 这里是append，因此计算完之后是反着的，之后需要倒过来

                returns = returns[::-1]   # 由于之前的计算append的，是反着的，因此我们将其倒过来即可
                returns = torch.tensor(returns)
                # 例如 returns = tensor([7.9411, 7.7123, 7.4581, 7.1757, 6.8619, 6.5132, 6.1258, 5.6953, 5.2170,
                # 4.6856, 4.0951, 3.4390, 2.7100, 1.9000, 1.0000])

                """ 将 returns 标准化，避免方差过大 """
                returns = (returns - returns.mean()) / (returns.std() + 1e-9)
                # 例如标准化后 returns = tensor([ 1.2303,  1.1263,  1.0107,  0.8823,  0.7396,  0.5810,  0.4049,  0.2092,
                # -0.0083, -0.2500, -0.5185, -0.8168, -1.1483, -1.5166, -1.9258])
                policy_net.update(returns, log_probs)

                print('Episode: {}, total reward: {}'.format(episode, total_reward_episode[episode]))

                break

            states.append(next_state)
            state = next_state

# 7. We specify the size of the policy network (input, hidden, and output layers), the
# learning rate, and then create a PolicyNetwork instance accordingly:

n_state = env.observation_space.shape[0]
n_action = env.action_space.n
n_hidden = 128
lr = 0.003
policy_net = PolicyNetwork(n_state, n_action, n_hidden, lr)

gamma = 0.9   # We set the discount factor as 0.9:

# 8. We perform learning with the REINFORCE algorithm using the policy network
# we just developed for 500 episodes, and we also keep track of the total rewards
# for each episode:

n_episode = 500
total_reward_episode = [0] * n_episode
reinforce(env, policy_net, n_episode, gamma)

# 9. Let's now display the plot of episode reward over time:
import matplotlib.pyplot as plt
plt.plot(total_reward_episode)
plt.title('Episode reward over time')

plt.xlabel('Episode')
plt.ylabel('Total reward')
plt.show()

警告信息

这里有几处会警告 ：

    def __init__(self, n_state, n_action, n_hidden=50,lr=0.001):
        self.model = nn.Sequential(
            nn.Linear(n_state, n_hidden),
            nn.ReLU(),
            nn.Linear(n_hidden, n_action),
            nn.Softmax(),
        )
        
...
...
probs = self.predict(torch.Tensor(s))

警告信息UserWarning: Implicit dimension choice for softmax has been deprecated. Change the call to include dim=X as an argument. input = module(input)

这个是因为：

这个警告的原因是softmax()函数已经被弃用了，虽然程序还是可以运行成功，但是这个做法不被pytorch所赞成。

这个写法在早期的pytorch版本是没有警告的，现在因为其他考虑，要加上有指明dim参数。

我们直接改为dim=-1即可，也就是

    def __init__(self, n_state, n_action, n_hidden=50, lr=0.001):
        self.model = nn.Sequential(
            nn.Linear(n_state, n_hidden),
            nn.ReLU(),
            nn.Linear(n_hidden, n_action),
            # nn.Softmax(),   # 这个写法在早期的pytorch版本是没有警告的，现在因为其他考虑，要加上有指明dim参数。
            nn.Softmax(dim=-1),
        )
        self.optimizer = torch.optim.Adam(self.model.parameters(), lr)
        # 这个loss比较麻烦，就不在这里定义了，在后面会计算
        

代码详解: reinforce函数剖析

• 注意，这个函数里直接把梯度下降迭代也都完成了。

强调： Reinforce算法其实就是一种batch操作。每一次reinforce，生成一个长度为T的轨迹trajectory （这个T是每一局游戏都不一样的，因为不确定多少步结束游戏），因此就相当于有T个transition，我们实际上是基于这T个transition去学习、更新网络。虽然是会合更新，但是其实也是一种batch操作。只不过batch size不固定而已。

# Now, we can move on to developing the REINFORCE algorithm with a policy network model:
def reinforce(env, policy_net, n_episode, gamma=1.0):
    """
    REINFORCE algorithm
    @param env: Gym environment
    @param estimator: policy network
    @param n_episode: number of episodes
    @param gamma: the discount factor
    """
    for episode in range(n_episode):
        log_probs = []  # 必须要，计算loss以及梯度下降用得到
        rewards = []    # 必须要，计算折扣回报returns以及梯度下降用得到
        actions = []    # 可删去，放在这里是为了debug方便
        states = []     # 可删去，放在这里是为了debug方便
        state = env.reset()
        states.append(state)   # 可删去，放在这里是为了debug方便
        while True:
            action, log_prob = policy_net.get_action(state)
            next_state, reward, is_done, _ = env.step(action)
            # if(is_done == True):
            #     print('DONE')    # 这个是为了调试用的，看一个episode
            total_reward_episode[episode] += reward  # total_reward_episode里面一个元素代表一个轨迹的总reward，主要是用来看看目前模型效果如何了

            log_probs.append(log_prob)  # 例如 log_probs = [-0.5651,-0.5807,-0.5959,-0.8173,-0.5932,-0.8210,-0.5895,-0.8286,-0.8165,-0.5679,-0.5757,-0.5504,-0.9293,-0.5300,-0.9650]
            rewards.append(reward)  # 例如rewards = [1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0] # 1*15个
            actions.append(action)  # 例如actions = [0, 0, 0, 1, 0, 1, 0, 1, 1, 0, 0, 0, 1, 0, 1]   # 1*15个

            """
                is_done == True
                这说明一个episode结束了，我们记录了一个轨迹的信息，接下来就是REINFORCE来计算评估的 u_t了
                这种方法是用一个轨迹去估计，这是一个无偏估计，是蒙特卡洛近似
                
                这里，其实只需要整个轨迹的reward，以及相应的 log_probs即可。例如
                rewards = [1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0] # 1*15个 
                log_probs = [tensor(-0.5651, grad_fn=<LogBackward>),
                             tensor(-0.5807, grad_fn=<LogBackward>),
                             tensor(-0.5959, grad_fn=<LogBackward>),
                             tensor(-0.8173, grad_fn=<LogBackward>),
                             tensor(-0.5932, grad_fn=<LogBackward>),
                             tensor(-0.8210, grad_fn=<LogBackward>),
                             tensor(-0.5895, grad_fn=<LogBackward>),
                             tensor(-0.8286, grad_fn=<LogBackward>),
                             tensor(-0.8165, grad_fn=<LogBackward>),
                             tensor(-0.5679, grad_fn=<LogBackward>),
                             tensor(-0.5757, grad_fn=<LogBackward>),
                             tensor(-0.5504, grad_fn=<LogBackward>),
                             tensor(-0.9293, grad_fn=<LogBackward>),
                             tensor(-0.5300, grad_fn=<LogBackward>),
                             tensor(-0.9650, grad_fn=<LogBackward>)]    # 1*15个 
            """
            if is_done:   # 这说明一个episode结束了
                returns = []
                U_t = 0
                gamma_pow = 0
                for reward in rewards[::-1]:   # 就是从后往前循环，计算u_T, u_{T-1}, ...., u_1
                    U_t += gamma ** gamma_pow * reward    # U_t = sum (gamma_pow * reward_t), 也就是我的笔记中的公式
                    gamma_pow += 1
                    returns.append(U_t)  # 这里是append，因此计算完之后是反着的，之后需要倒过来

                returns = returns[::-1]   # 由于之前的计算append的，是反着的，因此我们将其倒过来即可
                returns = torch.tensor(returns)
                # 例如 returns = tensor([7.9411, 7.7123, 7.4581, 7.1757, 6.8619, 	6.5132, 6.1258, 5.6953, 5.2170,
                # 4.6856, 4.0951, 3.4390, 2.7100, 1.9000, 1.0000])

                """ 将 returns 标准化，避免方差过大 """
                returns = (returns - returns.mean()) / (returns.std() + 1e-9)
                # 例如标准化后 returns = tensor([ 1.2303,  1.1263,  1.0107,  0.8823,  0.7396,  0.5810,  0.4049,  0.2092,
                # -0.0083, -0.2500, -0.5185, -0.8168, -1.1483, -1.5166, -1.9258])
                policy_net.update(returns, log_probs)

                print('Episode: {}, total reward: {}'.format(episode, total_reward_episode[episode]))

                break

            states.append(next_state)
            state = next_state

• episode: 一整轮游戏
• 我们debug,一整轮游戏后，is_done变为True，我们将这轮的轨迹：$$s_1,a_1,r_1,s_2,a_2,r_2,s_3,a_3,r_3,\cdots ,s_T,a_T,r_T$$，对应产生的log_probs 和rewards拿出来看一下：

强调： Reinforce算法其实就是一种batch操作。每一次reinforce，生成一个长度为T的轨迹trajectory （这个T是每一局游戏都不一样的，因为不确定多少步结束游戏），因此就相当于有T个transition，我们实际上是基于这T个transition去学习、更新网络。虽然是会合更新，但是其实也是一种batch操作。只不过batch size不固定而已。

states = 
[array([ 0.04387178, -0.01202765, -0.00428936,  0.03030406], dtype=float32),
 array([ 0.04363123, -0.20708783, -0.00368328,  0.32163057], dtype=float32),
 array([ 0.03948947, -0.40215713,  0.00274934,  0.61314964], dtype=float32),
 array([ 0.03144633, -0.5973174 ,  0.01501233,  0.9066973 ], dtype=float32),
 array([ 0.01949998, -0.4024019 ,  0.03314627,  0.6187704 ], dtype=float32),
 array([ 0.01145194, -0.5979708 ,  0.04552168,  0.9217058 ], dtype=float32),
 array([-5.0747546e-04, -4.0349251e-01,  6.3955799e-02,  6.4366937e-01],dtype=float32),
 array([-0.00857733, -0.59944475,  0.07682919,  0.955787  ], dtype=float32),
 array([-0.02056622, -0.40543556,  0.09594493,  0.68819726], dtype=float32),
 array([-0.02867493, -0.21176696,  0.10970887,  0.42719495], dtype=float32),
 array([-0.03291027, -0.40825784,  0.11825277,  0.7523491 ], dtype=float32),
 array([-0.04107543, -0.6047946 ,  0.13329975,  1.0797808 ], dtype=float32),
 array([-0.05317132, -0.8014005 ,  0.15489537,  1.4111475 ], dtype=float32),
 array([-0.06919933, -0.6085008 ,  0.18311831,  1.1706195 ], dtype=float32),
 array([-0.08136935, -0.8054693 ,  0.2065307 ,  1.5146688 ], dtype=float32)]   # 4*15个 

actions = [0, 0, 0, 1, 0, 1, 0, 1, 1, 0, 0, 0, 1, 0, 1]   # 1*15个 

rewards = [1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0] # 1*15个 

log_probs = [tensor(-0.5651, grad_fn=<LogBackward>),
 tensor(-0.5807, grad_fn=<LogBackward>),
 tensor(-0.5959, grad_fn=<LogBackward>),
 tensor(-0.8173, grad_fn=<LogBackward>),
 tensor(-0.5932, grad_fn=<LogBackward>),
 tensor(-0.8210, grad_fn=<LogBackward>),
 tensor(-0.5895, grad_fn=<LogBackward>),
 tensor(-0.8286, grad_fn=<LogBackward>),
 tensor(-0.8165, grad_fn=<LogBackward>),
 tensor(-0.5679, grad_fn=<LogBackward>),
 tensor(-0.5757, grad_fn=<LogBackward>),
 tensor(-0.5504, grad_fn=<LogBackward>),
 tensor(-0.9293, grad_fn=<LogBackward>),
 tensor(-0.5300, grad_fn=<LogBackward>),
 tensor(-0.9650, grad_fn=<LogBackward>)]    # 1*15个 

可以看到： 这相当于是选了一个batch size = 15的 batch，一次学习这一个batch，然后做一次参数更新。

这个log_probs 的计算方法是：

1. 先以神经网络经过softmax输出的概率， 比如probs = self.predict(torch.Tensor(s)) = [0.6, 0.4]，我们根据这个概率分布随机抽样出一个action，比如action = 0
2. 我们提取出action = 0对应的概率为0.6，我们取其对数$\log (0.6)$，这样就得到了一次的log_prob = log (0.6)
3. 由于这一个回合（episode ）进行了15步，那就又15个log_prob，因此log_prob就是1*15的，如上面展示的一样。

由于我们的策略梯度的公式是

1. 第1种：对每个动作a求和的形式：$$\begin{array}{r}\frac{\partial V(s;\theta )}{\partial \theta }=\sum _{a\in \mathcal{A}}\frac{\partial \pi (a|s;\theta )}{\partial \theta }\cdot Q_{\pi }(s,a)\end{array}$$
   这种形式适用于离散动作的情况，因为得对所有动作$a$都求导然后加和。
2. 第2种：$$\begin{array}{r}\frac{\partial V(s;\theta )}{\partial \theta }={\mathbb{E}}_{A\sim \pi (\cdot |s;\theta )}\left[\frac{\partial \log \pi (A|s;\theta )}{\partial \theta }\cdot Q_{\pi }(s,A)\right]\end{array}$$

方法1：REINFORCE

1. 我们让agent玩一局游戏，并且记录状态、动作、奖励的轨迹，也就是记录$$s_1,a_1,r_1,s_2,a_2,r_2,\cdots ,s_T,a_T,r_T.$$
   其中，$T$是最大的尝试次数，为了避免游戏一直结束不了。
2. 我们基于这个轨迹计算，对所有$t$，也就是$\forall t\in T$计算其折扣回报$$u_t=\sum _{k=t}^T{\gamma }^{k-t}{r}_k$$
3. 我们用$u_t$去近似$Q(s_t,a_t)$，也就是令$q_t=u_t$。这是因为$$Q_{\pi }(s_t,a_t)=\mathbb{E}[U_t]$$，因此，我们可以用随机变量$U_t$的一个实现值$u_t$去评估$Q(s_t,a_t)$，这也是无偏估计。

这也就是所谓的REINFORCE算法。

因此，我们来进行下面的操作：

$\forall t\in T$计算其折扣回报$$u_t=\sum _{k=t}^T{\gamma }^{k-t}{r}_k$$

代码中就是 （代码中为了避免折扣回报returns差别过大，导致收敛缓慢，特意做了标准化）

           if is_done:   # 这说明一个episode结束了
                returns = []
                U_t = 0
                gamma_pow = 0
                for reward in rewards[::-1]:   # 就是从后往前循环，计算u_T, u_{T-1}, ...., u_1
                    U_t += gamma ** gamma_pow * reward    # U_t = sum (gamma_pow * reward_t), 也就是我的笔记中的公式
                    gamma_pow += 1
                    returns.append(U_t)  # 这里是append，因此计算完之后是反着的，之后需要倒过来

                returns = returns[::-1]   # 由于之前的计算append的，是反着的，因此我们将其倒过来即可
                returns = torch.tensor(returns)
                # 例如 returns = tensor([7.9411, 7.7123, 7.4581, 7.1757, 6.8619, 	6.5132, 6.1258, 5.6953, 5.2170,
                # 4.6856, 4.0951, 3.4390, 2.7100, 1.9000, 1.0000])

                """ 将 returns 标准化，避免方差过大 """
                returns = (returns - returns.mean()) / (returns.std() + 1e-9)
                # 例如标准化后 returns = tensor([ 1.2303,  1.1263,  1.0107,  0.8823,  0.7396,  0.5810,  0.4049,  0.2092,
                # -0.0083, -0.2500, -0.5185, -0.8168, -1.1483, -1.5166, -1.9258])

最后的结果就是,15个时间点的$u_t,\forall t=1,2,\cdots ,15$如下

returns = tensor([7.9411, 7.7123, 7.4581, 7.1757, 6.8619, 6.5132, 6.1258, 5.6953, 5.2170,
        4.6856, 4.0951, 3.4390, 2.7100, 1.9000, 1.0000])

由于之后的return可能会误差很大，因此我们将其标准化

returns = (returns - returns.mean()) / (returns.std() + 1e-9)

returns = tensor([ 1.2303,  1.1263,  1.0107,  0.8823,  0.7396,  0.5810,  0.4049,  0.2092,
        -0.0083, -0.2500, -0.5185, -0.8168, -1.1483, -1.5166, -1.9258])

计算完了$u_t$，我们就完成了动作价值$Q(s,a)$的评估 （也就是我们已经用REINFORCE算法评估好了$u_t$），我们此时就要去计算策略梯度，然后更新网络参数了。我们进入update函数。

    # We now develop the training method, which updates the neural network with
    # samples collected in an episode:
    def update(self, returns, log_probs):
        """
        Update the weights of the policy network given the training samples
        @param returns: return (cumulative rewards) for each step in an episode
        @param log_probs: log probability for each step

		Note:
		--------
			return 是期望总价值的评估，是根据单步immediate reward计算的折扣回报
			Example：
				如果rewards = [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]  # 1 * 15，是一个做了15次的轨迹
				如果gamma = 0.9, 折扣回报计算结果为
				returns = tensor([7.9411, 7.7123, 7.4581, 7.1757, 6.8619, 	6.5132, 6.1258, 5.6953, 5.2170, 4.6856, 4.0951, 3.4390, 2.7100, 1.9000, 1.0000])
				log_probs: 是每一步执行动作的概率的log值，由于在Policy gradient中，reinforce我们是按照动作概率随机抽样
					比如probs=[0.6， 0.4]，我们抽样，得到action=0， reward=1,
					因此，我们actions.append(action); rewards.append(reward)
					并且，我们需要计算抽出的action对应的概率的log,也就是log(0.6)
					然后我们 log_probs.append(log(0.6))
					就是这样的操作
        """

        policy_gradient = []
        # 注意：这里policy_gradient是记录整个轨迹中所有transition下的分量loss，最后求和的
        # 比如：t=1, 第1个transition，loss_0 = -log_prob[0] * returns[0]
        # 比如：t=2, 第2个transition，loss_1 = -log_prob[1] * returns[1]
        # 最后求和：loss = loss_0 + loss_1 + ... + loss_T
        # 也就是下面的 loss = torch.stack(policy_gradient).sum()

        for log_prob, U_t in zip(log_probs, returns):
            policy_gradient.append(-log_prob * U_t)  # 求轨迹中单个transition的loss

        loss = torch.stack(policy_gradient).sum()   # 对轨迹中所有transition的loss求和，得到总loss

        self.optimizer.zero_grad()  # 在求导之前，先将前一步的导数清零，否则会叠加
        loss.backward()   # 反向传播求出参数的导数
        self.optimizer.step()  # 梯度下降更新神经网络参数

这里

log_probs = [tensor(-0.4983, grad_fn=<LogBackward>),
 tensor(-0.5083, grad_fn=<LogBackward>),
 tensor(-0.5101, grad_fn=<LogBackward>),
 tensor(-0.4873, grad_fn=<LogBackward>),
 tensor(-0.4430, grad_fn=<LogBackward>),
 tensor(-1.1343, grad_fn=<LogBackward>),
 tensor(-1.0506, grad_fn=<LogBackward>),
 tensor(-0.4643, grad_fn=<LogBackward>),
 tensor(-1.0850, grad_fn=<LogBackward>),
 tensor(-0.4437, grad_fn=<LogBackward>)]

# 经过标准化的returns如下
returns = tensor([ 1.2825,  1.0733,  0.8409,  0.5826,  0.2956, -0.0232, -0.3775, -0.7711,
        -1.2085, -1.6945])

由于我们要做梯度上升，因此要把loss变成

5. 设置策略网络的loss function为：
   $$\begin{array}{r}\text{loss function}=(\approx )-\left[\log \pi (\hat{a}|s;\theta )\right]\cdot q_t\end{array}$$

代码中就是

        for log_prob, U_t in zip(log_probs, returns):
            policy_gradient.append(-log_prob * U_t)  # 求轨迹中单个transition的loss

这一步操作之后，变成了

policy_gradient = [tensor(0.6391, grad_fn=<MulBackward0>),
 tensor(0.5456, grad_fn=<MulBackward0>),
 tensor(0.4289, grad_fn=<MulBackward0>),
 tensor(0.2839, grad_fn=<MulBackward0>),
 tensor(0.1310, grad_fn=<MulBackward0>),
 tensor(-0.0263, grad_fn=<MulBackward0>),
 tensor(-0.3966, grad_fn=<MulBackward0>),
 tensor(-0.3580, grad_fn=<MulBackward0>),
 tensor(-1.3112, grad_fn=<MulBackward0>),
 tensor(-0.7518, grad_fn=<MulBackward0>)]

其中，比如说第一个
$$0.6391=-(-0.4983\times 1.2825)=0.6391=-\left[\log \pi ({\hat{a}}_1=1|s_1;\theta )\right]\cdot u_1$$
这里${\hat{a}}_1=1$是我举的一个例子，这个${\hat{a}}_1=1$是在REINFORCE中在一轮游戏中，在$t=1$时刻，根据策略网络的输出概率(比如[0.52, 0.48]，随机抽样抽出来，得到${\hat{a}}_1=1$)。

另外，我们是对所有的这理论游戏中的时间点$t=1,2,3,\cdots ,T$，都计算一下策略梯度。

然后我们最终的loss需要设置成，这一个轨迹中，所有步的loss的总和要最小化。

也就是代码中的

        loss = torch.stack(policy_gradient).sum()   # 对轨迹中所有transition的loss求和，得到总loss

这里的逻辑是这样的，我们在一轮游戏中，执行了15个动作，然后我们的$u_t$也是评估了15次。这15次，每次都预测的很准，那说明策略很准。这个指标可以用这15次动作的误差的总和来衡量(就是一个标量，相当于当前目标函数值)。我们是想其越小越好。因此loss最终就等于这一个轨迹中所有时间节点上的policy loss的总和，也就是
$$\begin{array}{r}\text{total loss function}=(\approx )\sum _{t=1}^T-\left[\log \pi ({\hat{a}}_t|s_t;\theta )\right]\cdot u_t\end{array}$$
在本例中，
$$\begin{array}{rlr}\text{total loss function}& =0.6391+0.5456+0.4289+0.2839+0.1310+(-0.0263)+(-0.3966)+(-0.3580)+(-1.3112)+(-0.7518)& \\ =-0.8155& & \end{array}$$

代码执行结果也是如此

loss = torch.stack(policy_gradient).sum()   # 对轨迹中所有transition的loss求和，得到总loss

loss = tensor(-0.8155, grad_fn=<SumBackward0>)

然后，执行梯度下降 （对应原问题中的梯度上升，因为我们加了负号）

        self.optimizer.zero_grad()  # 在求导之前，先将前一步的导数清零，否则会叠加
        loss.backward()   # 反向传播求出参数的导数
        self.optimizer.step()  # 梯度下降更新神经网络参数

书中也有这部分介绍，可以看到，如果轨迹的长度为$T$，我们策略梯度就可以是对所有时间节点$t$的$-\left[\log \pi ({\hat{a}}_t|s_t;\theta )\right]\cdot u_t$的求和，也就是$$\Delta \theta =\alpha \sum _{t=1}^T\nabla \log \pi (a_t|s_t)\cdot G_t$$。跟上述总结的也是一致的。

---

作者：刘兴禄，清华大学，博士在读