【绘制】HTML5 Canvas 三次方贝塞尔曲线，bezierCureTo()的使用

我的处女作《Canvas系列教程》在我的Github上正在连载更新，希望能得到您的关注和支持，让我有更多的动力进行创作。

教程介绍、教程目录等能在README里查阅。

传送门：https://github.com/827652549/CanvasStudy

介绍

上一节，我们介绍了二次方贝塞尔曲线的用法。现在我们来介绍一下三次方贝塞尔曲线。

既然二次方贝塞尔曲线是向一个方向弯曲的曲线，那么三次方贝塞尔曲线则是向两个方向弯曲的曲线。

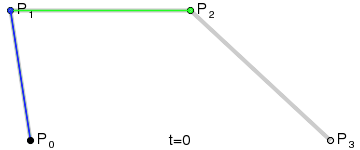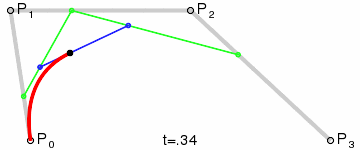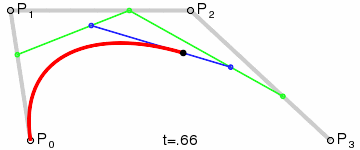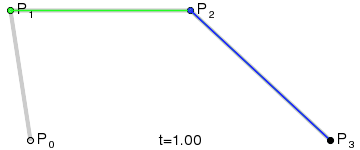
提示：三次贝塞尔曲线需要三个点。前两个点是用于三次贝塞尔计算中的控制点，第三个点是曲线的结束点。曲线的开始点是当前路径中最后一个点。如果路径不存在，那么请使用 beginPath() 和 moveTo() 方法来定义开始点。

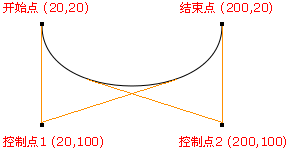
• 开始点：moveTo(20,20)
• 控制点 1：bezierCurveTo(20,100,200,100,200,20)
• 控制点 2：bezierCurveTo(20,100,200,100,200,20)
• 结束点：bezierCurveTo(20,100,200,100,200,20)

bezierCurveTo()方法的用法

方法	描述
bezierCurveTo(double cpx,double cpy,double cp2x,double cp2y,double x,double y)	创建一个代表三次方贝塞尔曲线的路径。你需要向该方法传入三个点的坐标，前两点是该曲线的控制点，最后一个是锚点。

 

绘制三次方贝塞尔曲线

上面两个图片例子是曲线开口向一个方向的，下面来实现一个开口向两个方向上的贝塞尔曲线。

在线演示  详细代码

 

贝塞尔曲线动态图片引用：https://www.cnblogs.com/hyb1/p/3875468.html