Internal Sorting: Quicksort-2: Sorting by Exchanging_the music of quicksort partitioning (by brad lyon)-CSDN博客

本文链接：https://blog.csdn.net/IOIO_/article/details/46288755

本文详细介绍了快速排序算法，包括动画演示、复杂度分析、算法流程、数据表和Java实现。特别指出，选择中间元素作为枢轴可以提高已排序或相同元素数组的排序效率。

摘要由CSDN通过智能技术生成

Quicksort-2:快速排序-2

Animation

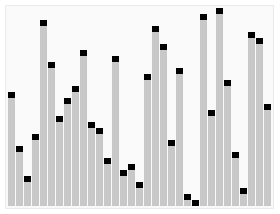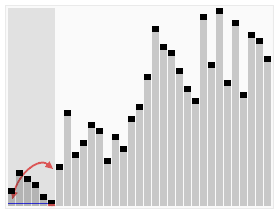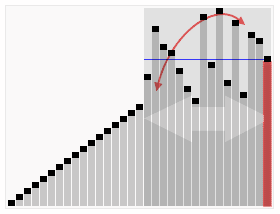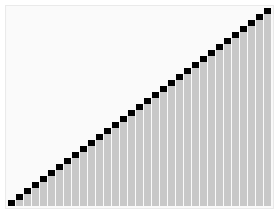
quick sort
Animated visualization of the quicksort algorithm. The horizontal lines are pivot values.

这里写图片描述
Full example of quicksort on a random set of numbers. The shaded element is the pivot. It is always chosen as the last element of the partition. However, always choosing the last element in the partition as the pivot in this way results in poor performance ( $O(n^2)$ ) on already sorted arrays, or arrays of identical elements. Since sub-arrays of sorted / identical elements crop up a lot towards the end of a sorting procedure on a large set, versions of the quicksort algorithm which choose the pivot as the middle element run much more quickly than the algorithm described in this diagram on large sets of numbers.

Complexity

Class	Sorting algorithm
Data structure	Array
Worst case performance	$O(n^2)$
Best case performance	$O(n \log n)$ (simple partition) or $O(n)$ (three-way partition and equal keys)
Average case performance	$O(n \log n)$
Worst case space complexity	$O(n)$ auxiliary (naive), $O(log n)$ auxiliary (Sedgewick 1978)

Algorithm Q

Algorithm Q (Quicksort). Records $R_1,... ,R_N$ are rearranged in place; after
sorting is complete their keys will be in order, $K_1<=...<=K_N$ . An auxiliary
stack with at most $\left \lfloor \lg N \right \rfloor$ entries is needed for temporary storage. This algorithm
follows the quicksort partitioning procedure described in the text above, with
slight modifications for extra efficiency:
a) We assume the presence of artificial keys $K_0 = -\infty$ and $K_{N+1} = +\infty$ such
that

$K_0<=K_i<=K_{N+1}$ for $1 <= i <= N$ . (13)

(Equality is allowed.)
b) Subfiles of $M$ or fewer elements are left unsorted until the very end of the
procedure; then a single pass of straight insertion is used to produce the final
ordering. Here $M >= 1$ is a parameter that should be chosen as described in
the text below. (This idea, due to R. Sedgewick, saves some of the overhead
that would be necessary if we applied straight insertion directly to each small
subfile, unless locality of reference is significant.)
c) Records with equal keys are exchanged, although it is not strictly necessary
to do so. (This idea, due to R. C. Singleton, keeps the inner loops fast and
helps to split subfiles nearly in half when equal elements are present; see
exercise 18.)
Q1. [Initialize.] If $N <= M$ , go to step Q9. Otherwise set the stack empty, and
set $l \leftarrow 1, r \leftarrow N$ .
Q2. [Begin new stage.] (We now wish to sort the subfile $R_l ... R_r$ ; from the
nature of the algorithm, we have $r >= l + M$ , and $K_{l-1} <= K_i <= K_{r+1}$ for
$l <= i <=r$ .) Set $i \leftarrow l, j \leftarrow r+1$ ; and set $K \leftarrow K_l$ . (The text below discusses
alternative choices for $K$ that might be better.)

$K_k<=K$ for $l-1 <= k <= i, K <= K_k$ for $j <= k <= r+1$ ; (14)

and $l <= i < j$ .) Increase $i$ by $1$ ; then if $K_i < K$ , repeat this step. (Since
$K_j >= K$ , the iteration must terminate with $i <= j$ .)
Q4. [Compare $K:K_j$ .] Decrease $j$ by $1$ ; then if $K < K_j$ , repeat this step. (Since
$K >= K_{i-1}$ , the iteration must terminate with $j >= i-1$ .)
Q5. [Test $i:j$ .] (At this point, (14) holds except for $k = i$ and $k = j$ ; also
$K_i >= K >= K_j$ , and $r >= j >= i-1 >= l$ .) If $j <= i$ , interchange $R_l \leftrightarrow R_j$ and
go to step Q7.
Q6. [Exchange.] Interchange $R_i \leftrightarrow R_j$ and go back to step Q3.
Q7. [Put on stack.] (Now the subfile $R_l ... R_j ... R_r$ has been partitioned so
that $K_k <= K_j$ for $l-1 <= k <= j$ and $K_j <= K_k$ for $j <= k <= r+1$ . If
$r-j >= j-l > M$ , insert $(j+1, r)$ on top of the stack, set $r \leftarrow j-1$ , and go
to Q2. lf $j-l > r-j > M$ , insert $(l, j-1)$ on top of the stack, set $l \leftarrow j+1$ ,
and go to Q2. (Each entry $(a, b)$ on the stack is a request to sort the subfile
$R_a ... R_b$ at some future time.) Otherwise if $r-j > M >= j-l$ , set $l \leftarrow j+1$
and go to Q2; or if $j-l > M >= r-j$ , set $r \leftarrow j-1$ and go to Q2.
Q8. [Take off stack.] If the stack is nonempty, remove its top entry $(l', r')$ , set
$l \leftarrow l', r \leftarrow r'$ , and return to step Q2.
Q9. [Straight insertion sort.] For $j = 2, 3, ..., N$ , if $K_{j-1} > K_j$ do the following
operations: Set $K \leftarrow K_j, R \leftarrow R_j, i \leftarrow j-1$ ; then set $R_{i+1} \leftarrow R_i$ and
$i \leftarrow i-1$ one or more times until $K_i <= K$ ; then set $R_{i+1} \leftarrow R$ . (This
is Algorithm 5.2.1S, modified as suggested in exercise 5.2.1-10 and answer
5.2.1-33. Step Q9 may be omitted if $M = 1$ . Caution: The final straight
insertion might conceal bugs in steps Q1-Q8; don’t trust an implementation
just because it gives the correct answers!) |

Flow diagram

Quicksort-2:Sorting by Exchanging:Internal Sorting

Data table

这里写图片描述

Java program

In this program, R1,…,RN were simplified to K1,…,KN.

/**
 * Created with IntelliJ IDEA.
 * User: 1O1O
 * Date: 12/3/13
 * Time: 10:01 PM
 * :)~
 * Quicksort-2:Sorting by Exchanging:Internal Sorting
 */
public class Main {

    public static void main(String[] args) {
        int N = 16;
        int[] K = new int[18];
        int[] L = new int[5];   /*Space at most Math.floor(Math.log(N)/Math.log(2))*/
        int[] R = new int[5];   /*Space at most Math.floor(Math.log(N)/Math.log(2))*/
        int len = 0;
        int M = 4;
        int temp;

        /*Prepare the data*/
        K[0] = -10000;              /*Negative Infinity*/
        K[1] = 503;
        K[2] = 87;
        K[3] = 512;
        K[4] = 61;
        K[5] = 908;
        K[6] = 170;
        K[7] = 897;
        K[8] = 275;
        K[9] = 653;
        K[10] = 426;
        K[11] = 154;
        K[12] = 509;
        K[13] = 612;
        K[14] = 677;
        K[15] = 765;
        K[16] = 703;
        K[17] = 10000;              /*Positive Infinity*/

        /*Output unsorted Ks*/
        System.out.println("Unsorted Ks:");
        for(int i=1; i<=N; i++){
            System.out.println(i+":"+K[i]);
        }
        System.out.println();

        /*Kernel of the Algorithm!*/
        int l;
        int r;
        int i;
        int j;
        int Key;
        boolean stackEmpty = false;

        if(N > M){
            len = 0;
            l = 1;
            r = N;

            do{
                i = l;
                j = r+1;
                Key = K[l];

                do{
                    do{
                        i++;                  /*Q3*/
                    }while (K[i] < Key);

                    do{
                        j--;                    /*Q4*/
                    }while (Key < K[j]);

                    if(j <= i){                      /*Q5*/
                        temp = K[l];
                        K[l] = K[j];
                        K[j] = temp;

                        if(r-j >= j-l && j-l > M){                /*Q7*/
                            len++;
                            L[len] = j+1;
                            R[len] = r;
                            r = j-1;
                            break;
                        }else if(j-l > r-j && r-j > M){
                            len++;
                            L[len] = l;
                            R[len] = j-1;
                            l = j+1;
                            break;
                        }else if(r-j > M && M >= j-l){
                            l = j+1;
                            break;
                        }else if(j-l > M && M >= r-j){
                            r = j-1;
                            break;
                        }
                        if(len != 0){                   /*Q8*/
                            l = L[len];
                            r = R[len];
                            len--;
                        }else {
                            stackEmpty = true;
                        }
                        break;
                    }else {
                        temp = K[i];                /*Q6*/
                        K[i] = K[j];
                        K[j] = temp;
                    }
                }while (true);
            }while (!stackEmpty);

            for(j=2; j<=N; j++){               /*Q9*/
                if(K[j-1] > K[j]){
                    Key = K[j];
                    i = j-1;
                    do{
                        K[i+1] = K[i];
                        i--;
                        if(i == 0){
                            break;
                        }
                    }while (K[i] > Key);
                    K[i+1] = Key;
                }
            }
        }else {
            for(j=2; j<=N; j++){                 /*Q9*/
                if(K[j-1] > K[j]){
                    Key = K[j];
                    i = j-1;
                    do{
                        K[i+1] = K[i];
                        i--;
                        if(i == 0){
                            break;
                        }
                    }while (K[i] > Key);
                    K[i+1] = Key;
                }
            }
        }

        /*Output sorted Ks*/
        System.out.println("Sorted Ks:");
        for(i=1; i<=N; i++){
            System.out.println(i+":"+K[i]);
        }
    }
}

Outputs

Unsorted Ks:
1:503
2:87
3:512
4:61
5:908
6:170
7:897
8:275
9:653
10:426
11:154
12:509
13:612
14:677
15:765
16:703

Sorted Ks:
1:61
2:87
3:154
4:170
5:275
6:426
7:503
8:509
9:512
10:612
11:653
12:677
13:703
14:765
15:897
16:908