师曰:鉴于高年级同学乃至很多研究生,几乎是谈“矩阵”色变,“计算机要从娃娃抓起”嘛,所以近两年给你们新增“矩阵运算”这一章。矩阵运算在机器学习等领域具有非常重要的应用。今天这节课温故而知新,帮助你们为往后的课程奠定基础,更重要的是你们要克服恐惧心理。
基础概念
符号标识
矩阵:大写字母,如A,B;
矩阵的转置:A
T
^T
T;
向量:小写字母,如
x
x
x,
y
y
y;
单位向量:e
i
_i
i【除第
i
i
i个元素为1之外其他元素均为0的向量】;
零矩阵:0 【所有元素都为0的矩阵,零和零矩阵虽然表示方法一样,但是意义截然不同】;
对角矩阵:diag(
a
11
a_{11}
a11,
a
22
a_{22}
a22,···,
a
n
n
a_{nn}
ann)【
a
i
j
=
0
a_{ij}=0
aij=0,
i
i
i!=
j
j
j时】;
单位矩阵:
I
n
I_n
In=diag(
1
1
1,
1
1
1,···,
1
1
1)【对角线元素为1,其它元素为0】;
三对角矩阵:
T
T
T;
上三角矩阵:
U
U
U【对角线以下(不包含对角线)的元素均为0】;
下三角矩阵:
L
L
L【对角线以上(不包含对角线)的元素均为0】;
置换矩阵:
P
P
P【每行每列均只有一个1,其它元素为0的矩阵。也称“排列矩阵”】;
对称矩阵:【满足A=A
T
^T
T的矩阵】;
基本操作:
矩阵加减法:两个同型矩阵 A 和 B【意即均为mXn矩阵】对应位置上的元素进行加减。(这里注意是所有元素,很容易和行列式搞混)
矩阵乘法:两个相容矩阵 A 和 B【意即前者的列数等于后者的行数】相乘得到的矩阵 C 中的元素
c
i
j
=
∑
k
=
1
n
a
i
k
b
k
j
c_{ij} = \sum_{k=1}^n a_{ik} b_{kj}
cij=∑k=1naikbkj,
矩阵乘法满足结合律:A(BC)=(AB)C
矩阵乘法满足分配律:A(B+C)=AB+AC
矩阵乘法不满足结合率:AB != BA
基本性质:
矩阵的逆:A
−
1
^{-1}
−1(如果存在),AA
−
1
^{-1}
−1=
I
n
I_n
In=A
−
1
^{-1}
−1A。
没有逆的矩阵称之为不可逆的,或奇异的;
若矩阵有逆,则称之为可逆的,或非奇异的;
线性相关:如果存在不全为0的相关系数
c
1
c_1
c1,
c
2
c_2
c2,···,
c
n
c_n
cn,使得
c
1
x
1
c_1x_1
c1x1+
c
1
x
1
c_1x_1
c1x1+···+
c
1
x
1
c_1x_1
c1x1=0,则称向量
x
1
x_1
x1,
x
2
x_2
x2,···,
x
n
x_n
xn 是线性相关的。
线性无关:若向量组不是线性相关的,那么它们就是线性无关的。
矩阵的秩:矩阵A的最大线性无关行或列集合的大小。
矩阵【方阵】存在逆说明该矩阵是满秩的,秩的大小等于该矩阵行或。列的大小。
矩阵的空向量:满足 A
x
x
x=0 的非零向量
x
x
x。矩阵存在逆,就不存在空向量。
子矩阵:
A
[
i
j
]
A_{[ij]}
A[ij], 删除矩阵A中
i
i
i行
j
j
j列后得到的 n-1 阶矩阵。
代数余子式:
(
−
1
)
i
+
j
d
e
t
(
A
[
i
j
]
)
(-1)^{i+j} det(A_{[ij]})
(−1)i+jdet(A[ij]), 其中
d
e
t
(
A
[
i
j
]
)
det(A_{[ij]})
det(A[ij])代表行列式。
行列式:
d
e
t
(
A
)
det(A)
det(A)。递归定义
n=1时,
d
e
t
(
A
)
=
a
11
det(A)=a_{11}
det(A)=a11
n!=1时,
d
e
t
(
A
)
=
∑
j
=
1
n
(
−
1
)
i
+
j
a
1
j
d
e
t
(
A
[
1
j
]
)
det(A)=\sum_{j=1} ^n (-1)^{i+j}a_{1j}det(A_{[1j]})
det(A)=∑j=1n(−1)i+ja1jdet(A[1j])
- 当行列式等于0时,矩阵不存在逆。
- 交换A的任意两行或两列,矩阵改变正负号。
- 矩阵A的行列式与其转置矩阵的行列式相等, d e t ( A ) = d e t ( A T ) det(A)=det(A^T) det(A)=det(AT)。
- 任意两个方阵乘积的行列式等于它们分别的行列式相乘, d e t ( A B ) = d e t ( A ) d e t ( B ) det(AB)=det(A)det(B) det(AB)=det(A)det(B)。
- 矩阵A的某一行或某一列的每个元素乘以λ时,行列式乘以λ。
如果矩阵某行或某列全为0,则行列式为0。
正定矩阵:如果 n阶矩阵A满足对于所有 n向量
x
≠
0
x\neq0
x̸=0,有
x
T
A
x
>
0
x^TAx>0
xTAx>0,则称A是正定的。实际应用中遇到的矩阵通常都是正定的。
对于任意列满秩的矩阵A,矩阵
A
T
A
A^TA
ATA都是正定的。
矩阵运算
1. LUP分解求解线性方程组 A x = b Ax=b Ax=b
为什么选择LUP分解方法解线性方程组?理由很简单:由于计算机存储数据的特性导致矩阵在求逆过程中会有数值不稳定的问题, 即在计算机计算过程中, 除以0可能会造成溢出。LUP分解方法具有数值稳定性,且在实践中运行速度更快。
LUP分解背后的思想就是找出三个 n阶矩阵 L , U , P L, U, P L,U,P,满足 P A = L U PA=LU PA=LU。 L , U , P L, U, P L,U,P被称作矩阵A的LUP分解。
LU分解
那么如何求解
L
,
U
,
P
L, U, P
L,U,P呢?在求解LUP之前,我们先来简化运算,将P视为单位矩阵,则上式
A
=
L
U
A=LU
A=LU,
L
L
L和
U
U
U称为矩阵A的一个LU分解。
高斯消元法
创建LU分解的方法之一是高斯消元法(Gaussian elimination).
- 首先从其它方程中减去第一方程的倍数,以把那些方程中的第一个变量消去;
- 然后从第三个及以后的方程中减去第二个方程的倍数,以把这些方程的第二个变量消去;
- 同理,直至消去从最后一个方程中减去倒数第二个方程的倍数,以把最后一个方程的倒数第二个变量消去。
- 这样就获得了正对角线以下所有元素为0的矩阵,实际上此矩阵就是U。矩阵L则是由消去变量所用的行的乘数所组成。
如果高斯消元法没说清楚可以看例子:【抱歉,例子写错了。。。有空再改回来】
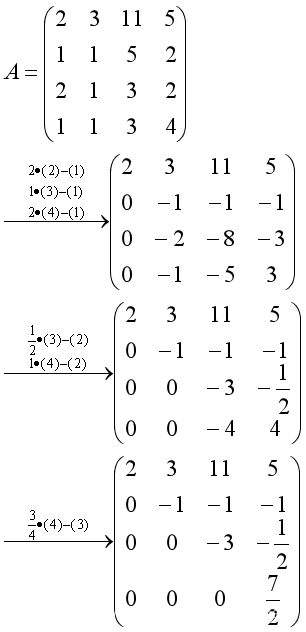
计算得到的矩阵就是上三角矩阵U

消去变量所用的行的乘数构成下三角矩阵L,其中对角线部分为1.
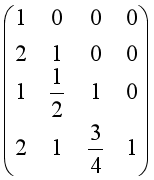
递归算法
n = 1时,选择L为单位矩阵,那么A=U,完成LU分解;
n > 1时,把A拆成四部分:
【注意:这里我们默认
a
11
!
=
0
a{11}!=0
a11!=0,因为接下来会有除以0的问题】
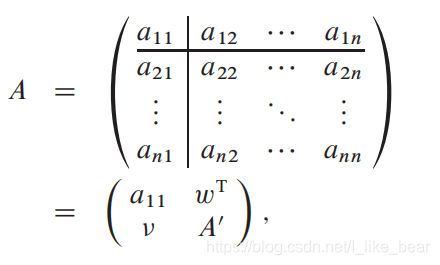
下边的符号是上边的向量、矩阵的标识。
然后就可以把A继续分解:
【血泪史:作为数学很差的我,曾经在线性代数期末考试填空题的第五题考到这道题,花了四十分钟分解也没分解出个所以然来。所以我其实很好奇第一个分解出来的人是怎么分解的?】

所得 A ′ − v w T / a 11 A' - vw^T/a_{11} A′−vwT/a11成为对于 a 11 a{11} a11的舒尔补(Schur Complement)。
递归的找到舒尔补的LU分解, A ′ − v w T / a 11 = L ′ U ′ A' - vw^T/a_{11}=L'U' A′−vwT/a11=L′U′
以下是证明递归算法是真的靠谱的。

LU分解图示
当然,上述理论和公式略微抽象,因此图示法来深入理解以下LU分解:[LU分解的运行过程–递归解法]

- 如(a)图所示,矩阵A亮相;
- 如( b )图所示,通过第一步, 图(a)中第一行【即(2 3 1 5)】不变, 第一列除第一行【即(2)】外的其它数字【即(6 2 4)】通过除以第一个数字【即图(b)中阴影处的(2)】,变成了图(b)中的(3 1 2). 其它行列的数字是通过图(a)中的数字减去该行该列所对应的变换后的第一个数字的乘积获得的.
比如第二行第二个数字 a 22 a_{22} a22【即图(a)中的(13), 图(b)中的(4)】,变换后的第一个数字分别是 a 21 a_{21} a21【即图(b)中的(3)】和 a 12 a_{12} a12【即图(b)中的(3)】,13-33=4,因此图(b)中=4.
再比如第四行第四个数字 a 44 a_{44} a44【即图(a)中的(31), 图(b)中的(21)】,变换后的第一个数字分别是 a 41 a_{41} a41【即图(b)中的(2)】和 a 14 a_{14} a14【即图(b)中的(5)】,31-25=21,因此图(b)中=21. - 如( c )图所示,具体同图(a)到图(b)差不多,不同点在于浅阴影的部分成为了新的"首行首列",深阴影的部分成了新的" a 11 a_{11} a11"
- 如( e )图所示,U是折线以上的部分,包括正对角线上的数字; L则包括折现以下的部分,正对角线上的数字设置为1.
伪代码
根据上述递归策略设计, 用一个迭代循环取代了递归过程. 这一转换是对"尾递归"过程进行标准的优化处理.
( 鉴于我大一开始就没学好尾递归, 导致我到现在看到计算机系统基础里面尾递归的汇编代码就发怵, 有空再深入了解其中的优化原理.)

Java实现
输入矩阵可以计算出具体的L和U: [当然就是依靠强大的伪代码,一步就运行出来的结果]
package LPU;
import java.util.Scanner;
/**
* User:Admin
* Date:2018/12/10
* Time:19:11
* Author:PiJiang
* Note: This is to create an LU-Composition
*
* 上三角矩阵 U: upper triangular matrix
* 下三角矩阵 L: lower triangular matrix
*
2 3 1 5
6 13 5 19
2 19 10 23
4 10 11 31
*
*/
public class LUDecomposition {
public static void main(String[] args) {
LUDecomposition l = new LUDecomposition();
l.luDecomposition(l.inputMatrix());
}
private int[][] inputMatrix(){
int[][] inputMatrix = new int[4][4];
Scanner input = new Scanner(System.in);
for (int i = 0; i < 4; i++) {
for (int j = 0; j < 4; j++) {
inputMatrix[i][j] = input.nextInt();
}
}
return inputMatrix;
}
// Computing an LU Decomposition
private void luDecomposition(int[][] matrix){
int n = matrix.length; // the order of the matrix
int[][] upperTriangularMatrix = new int[n][n]; // create U -- a new n-order matrix
int[][] lowerTriangularMatrix = new int[n][n]; // create L -- a new n-order matrix
// 实际上,以下需要变成 0 的元素,它们被初始化后的值就是 0, 写下这一步主要是为了提醒自己
// initialize U with 0s below the diagonal
for (int i = 0; i < n; i++) {
for (int j = i + 1; j < n; j++) { // [0,0] NO, [0,1] NO, [1,0] OK
upperTriangularMatrix[j][i] = 0;
}
}
// initialize L with 0s above the diagonal and 1s on the diagonal
for (int i = 0; i < n; i++) {
for (int j = i; j < n; j++) {
if(j == i){
lowerTriangularMatrix[j][i] = 1;
}else{
lowerTriangularMatrix[j][i] = 0;
}
}
}
for (int k = 0; k < n; k++) {
upperTriangularMatrix[k][k] = matrix[k][k]; // 将主对角线的值赋给上三角矩阵,作为朝代更迭依旧江山不老的“a11”
for (int i = k + 1; i < n; i++) {
lowerTriangularMatrix[i][k] = matrix[i][k] / upperTriangularMatrix[k][k];
upperTriangularMatrix[k][i] = matrix[k][i];
}
for (int i = k + 1; i < n; i++) {
for (int j = k + 1; j < n; j++) {
matrix[i][j] = matrix[i][j] - lowerTriangularMatrix[i][k] * upperTriangularMatrix[k][j];
}
}
}
}
}
LUP分解
依前文所述,为了求解线性方程组,应当避免在LUP分解中把被除数选作为0或接近于0的极小值,所以尽可能选择一个较大的主元。置换矩阵存在的意义就是把可能存在的0置换出去。
【关于大小之争,有同学在上课的时候质疑老师:为什么要取最大值,正无穷也可以吗?各位看官有何见解呢?
老师的回复是:首先,正无穷出现的机率很小,或者说是不可能出现正无穷的;其次取最大值肯定比取最小值要好,取最大值绝对不会溢出,但最小值就很容易溢出。】
和LU分解一样,LUP分解也是递归进行的。不同的是,加入了置换矩阵来改变矩阵A中主元使其变成该列中的最大值,从而不存在0变成被除数的现象【非奇异矩阵每一列至少存在一个不为零的数值】。相应地,LUP分解过程中的列向量 v / s k 1 v/s_{k1} v/sk1和舒尔补都要乘以置换矩阵。
LUP分解的过程:

其实过程和LU分解一模一样,值得注意的是每次置换出最大主元的时候,一整列元素都要跟着换。
伪代码:

矩阵求逆待续。。。
Java实现
LUP分解求解线性方程组
了解了LUP分解方法的原理,解决线性方程组问题就更容易了。





















 8683
8683











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








