【数学建模笔记】2.整数规划

最新推荐文章于 2024-09-09 20:02:40 发布

Imagine_cc

最新推荐文章于 2024-09-09 20:02:40 发布

阅读量1.1w

点赞数 26

文章标签：数学建模

本文链接：https://blog.csdn.net/Imagine_cc/article/details/123155974

版权

本文详细解析了整数规划的基本概念，包括定义、分类特点和数学模型，重点介绍了纯整数规划、全整数规划和混合整数规划的区别。此外，探讨了整数线性规划的求解方法，如分枝定界法、割平面法、0-1规划和指派问题实例。适合对整数规划感兴趣的读者深入理解与实践应用。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

一、整数规划

1.定义：

规划中的变量（部分或全部）限制为整数时，称为整数规划。若在线性规划模型中，变量限制为整数，则称为整数线性规划。

2. 整数规划的分类

如不加特殊说明，一般指整数线性规划。大致可分为两类：

（1）变量全限制为整数时，称纯（完全）整数规划。

（2）变量部分限制为整数的，称混合整数规划。

3.特点：

1 原线性规划有最优解，当自变量限制为整数后，其整数规划解出现下述情况

（1）原线性规划最优解全是整数，则整数规划最优解与线性规划最优解一致。

（2）整数规划无可行解。

（3）有可行解（当然就存在最优解），但最优解值变差。

2 整数规划最优解不能按照实数最优解简单取整而获得

例 1：（建厂问题）某公司计划在 m 个地点建厂，可供选择的地点有 A 1 , A2 … A m ，他们的生产能力分别是 a 1 , a 2 , … a m （假设生产同一产品）。第 i 个工厂的建设费用为 f i ( i =1.2…m), 又有 n 个地点 B 1 , B 2 , … B n 需要销售这种产品，其销量分别为b 1 , b 2 … b n 。从工厂运往销地的单位运费为 C ij 。试决定应在哪些地方建厂，即满足各地需要，又使总建设费用和总运输费用最省？

4.整数规划的数学模型

一般形式：

$max(min)\, z=\sum_{j=1}^{n}c_{j}x_{j}$

$s.t.\left\{\begin{matrix} \sum_{j=1}^{n}a_{ij}x_{j}\leqslant (=,\geqslant )b_{i}\,\, \, \, \, \, (i=1,2,....m)\\ x_{j}\geq 0, \ \, \, \, \, (j=1,2,.....n) \end{matrix}\right.$ $x_{j}$ 为整数

依照决策变量取整要求的不同，整数规划可分为 纯整数规划、全整数规划、混合整数规划、0-1 整数规划。

纯整数规划：所有决策变量要求取非负整数（这时引进的 松弛变量 和 剩余变量 可以不要求整数）

在线性规划中，一个大于等于约束条件中超过资源或能力最底限的部分称之为剩余量。对于 $2x_{1}+x_{2}\leqslant 400$ ，假如最优解为（150,110）那么剩余量就为10。

类似地，在线性规划中，小于等于约束条件中未被使用的资源或能力的值成为松弛量。对于 $x_{1}+x_{2}\leq 300$ ，假如最优解为（150,140）那么本约束的松弛量就为10。

全整数规划：除了所有决策变量要求取非负整数外，系数aij和常数bi也要求取整数（这时引进的松弛变量和剩余变量也必须是整数）。

混合整数规划：只有一部分的决策变量要求取非负整数，另一部分可以取非负实数。

0-1整数规划(工作安排、分配）：所有决策变量只能取 0 或 1 两个整数。

二、整数线性规划的求解方法

从数学模型上看整数规划似乎是线性规划的一种特殊形式，求解只需在线性规划的基础上，通过舍入取整，寻求满足整数要求的解即可。但实际上两者却有很大的不同，通过舍入得到的解（整数）也不一定就是最优解，有时甚至不能保证所得到的解是整数可行解。

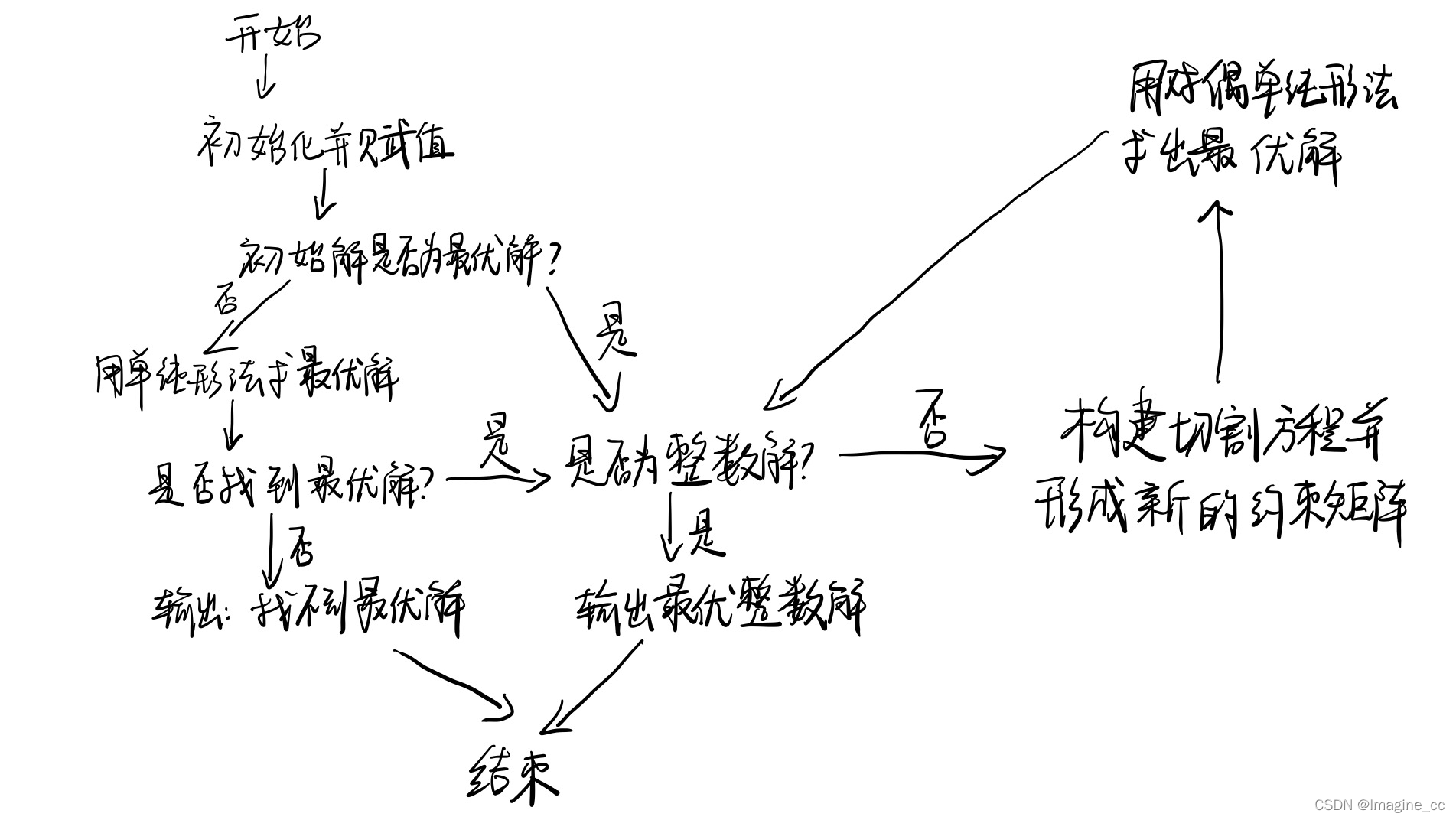
1.分枝定界法

不考虑整数限制先求出相应松弛问题的最优解，（不考虑整数）

若松弛问题无可行解，则ILP 无可行解；

若求得的松弛问题最优解符合整数要求，则是 ILP 的最优解；

若不满足整数条件，则任选一个不满足整数条件的变量 $x{_{i}}^{0}$ 来构造新的约束添加到松弛问题中形成两个子问题:

$x_{i}\leqslant [x{_{i}}^{0}];\, \, x_{i}\geqslant [x{_{i}}^{0}]+1$ (xi向下取整or向上取整作为上下界，添加约束）

依次在缩小的可行域中求解新构造的线性规划的最优解，并重复上述过程，直到子问题无解或有整数最优解。

例1：

例2：

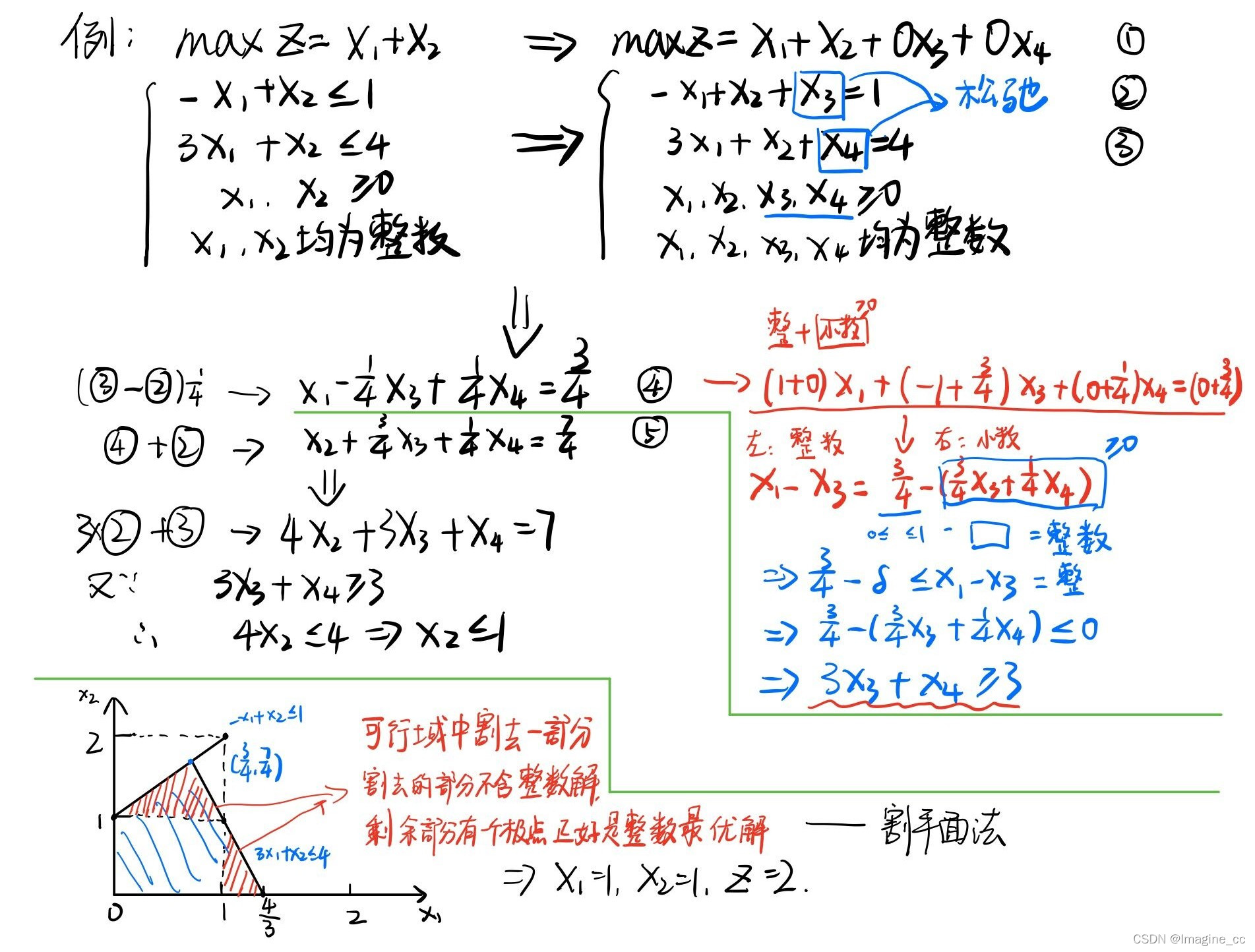
2.割平面法

基本思想：

1.如果松弛问题（P0）无解，则（P）无解；

2.如果（P0）的最优解为整数向量，则也是（P）的最优解；

3.如果（P0）的解含有非整数分量，则对（P0）增加割平面条件：即对（P0）增加一个线性约束，将（P0）的可行域割掉一块，使得非整数解恰好在割掉的一块中，但又没有割掉原问题（P）的可行解，得到问题（P1），重复上述的过程。

例1：

基本步骤：

程序流程：

3.0-1规划

例1：0-1变量的使用

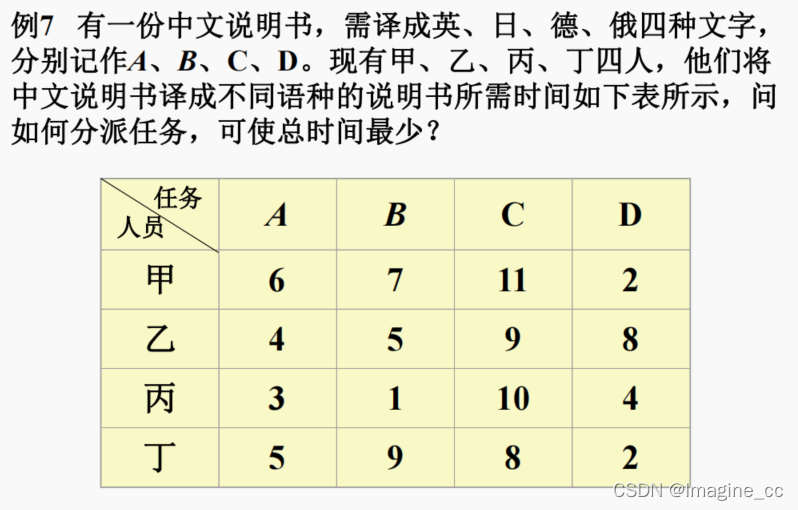
投资问题：有600万元投资五个项目，收益如表，求利润最大的方案？

例2：互斥约束问题

例3：固定费用问题

4.指派问题

数学模型：

非标准形式的指派问题：

1.最大化指派问题：

$C=(c_{ij})_{n\times n}$ 中最大元素为m，令 $B=(b_{ij})_{n\times n}=(m-c_{ij})_{n\times n}$

2.人数和工作数不等

人少工作多：添加虚拟的“人”，代价都为0

人多工作少：添加虚拟的工作，代价都为0

3.一个人可做多件工作

该人可化为几个相同的“人”

4.某工作一定不能由某人做

该人该工作的相应代价取足够大M

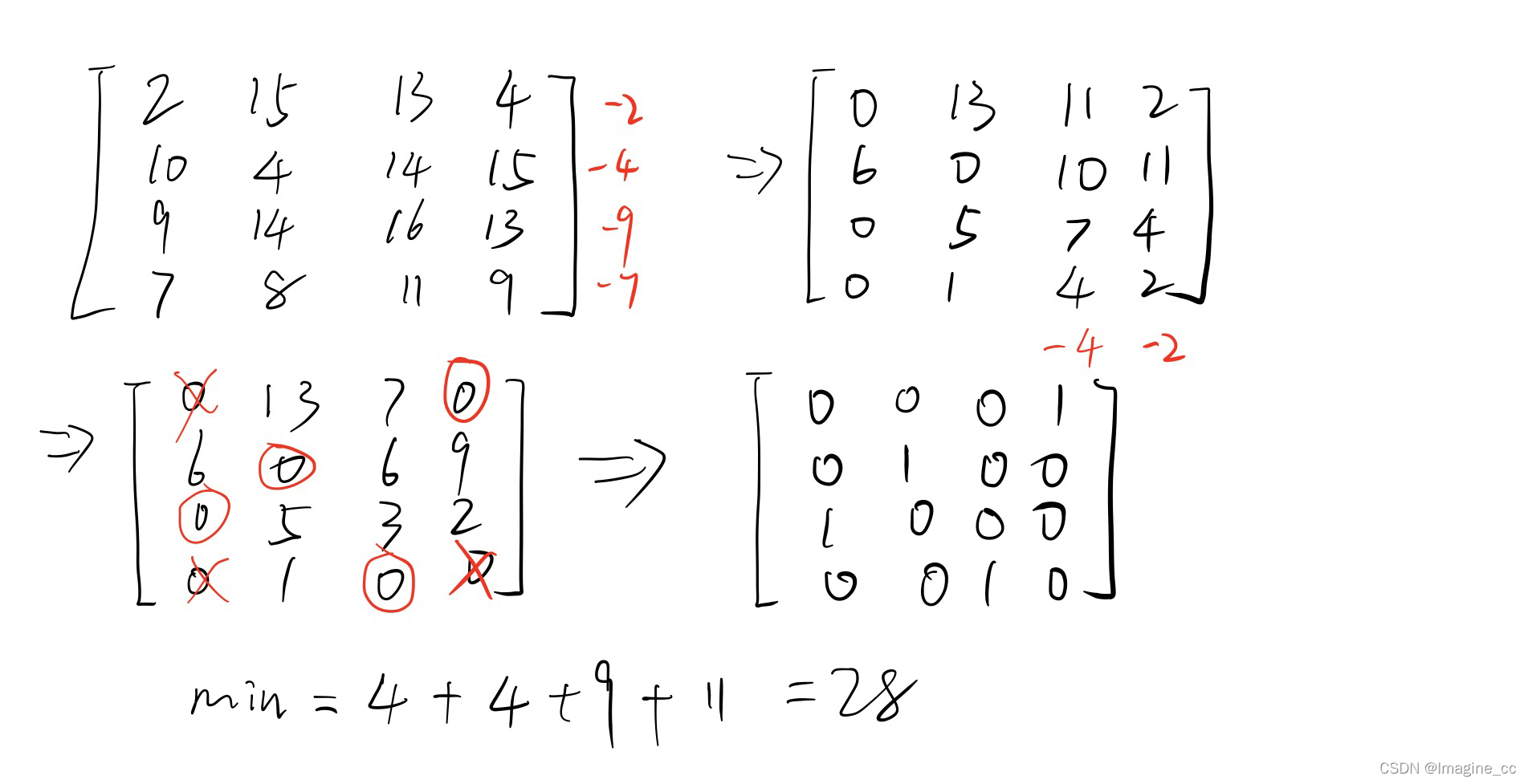
匈牙利算法：

参考：指派问题：匈牙利算法_Wonz-CSDN博客_匈牙利算法指派问题

例1：

例2：

例3：

$\begin{bmatrix} 3 & 8 & 2 &10 &3 \\ 8 & 7 & 2 &9 &7 \\ 6& 4 &2 &7 &5 \\ 8& 4&2 &3 &5 \\ 9 & 10&6 & 9 &10 \end{bmatrix}$

c=[3,8,2,10,3;8,7,2,9,7;6,4,2,7,5;8,4,2,3,5;9,10,6,9,10];
c=c(:); %把矩阵c转换成向量
a=zeros(10,25); %10个方程（行+列），25个未知数
for i=1:5
    a(i,(i-1)*5+1:5*i)=1;
    a(5+i,i:5:25)=1;
end %此循环把指派问题转化为线性规划问题
b=ones(10,1);
[x,y]=linprog(c,[],[],a,b,zeros(25,1),ones(25,1));
X=reshape(x,5,5) %重构成矩阵
opt=y