全连接网络原理

全连接网络原理

上一期介绍了只包含单隐层的浅层全连接网络，本期介绍更具有普遍性的深层全连接网络。推荐先看一下上期的内容，将更有助于理解。上一期的链接为：
https://blog.csdn.net/Iseno_V/article/details/102941210
公式推导部分依旧采用截图的形式，如果需要源文档可以给我留言。

1. 网络结构图

下图为一个2分类问题的四层结构全连接网络。

2. 原理详解

2.1 参数约定

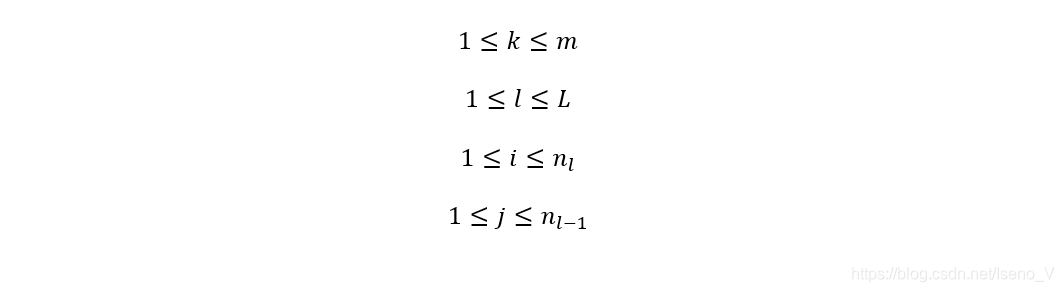
2.2 前向传播过程

2.3 反向传播过程

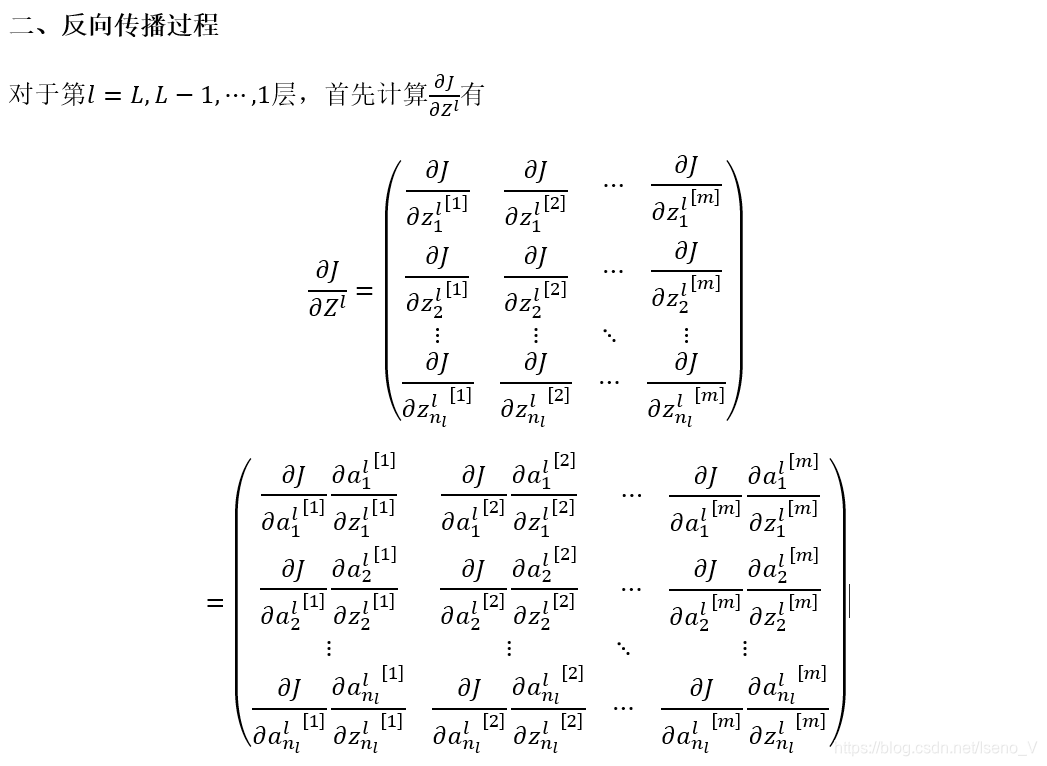
2.4 算法总结

3. 代码实现

整个全连接网络的源代码架构如下图所示：

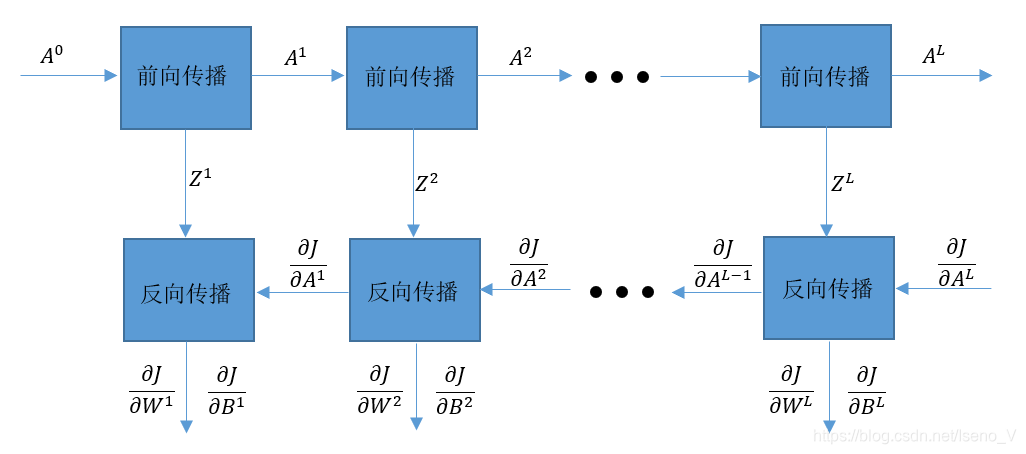
python代码实现为：

# -*- coding: utf-8 -*-
"""
Created on Wed Nov 13 19:59:16 2019

@author: Iseno_V
"""

import numpy as np

#生成训练和测试数据
#数据为二维的点，以原点在圆心半径为5的圆为分界线，来区分正负样本
#形参：m为数据集大小
#返回值：返回数据和标签
def createData(m):
    X1 = np.zeros([2,int(m/2)])
    X2 = np.zeros([2,int(m/2)])
    L1 = 0
    L2 = 0
    while L1<m/2:
        a = np.random.rand(1,1)*10
        b = np.random.rand(1,1)*10
        if a**2+b**2<=25:
            X1[0,L1]=a
            X1[1,L1]=b
            L1+=1
    while L2<m/2:
        a = np.random.rand(1,1)*10
        b = np.random.rand(1,1)*10
        if a**2+b**2>25:
            X2[0,L2]=a
            X2[1,L2]=b
            L2+=1
    X=np.hstack((X1,X2))
    Y=np.hstack((np.zeros((1,int(m/2))),np.ones((1,int(m/2)))))
    return X,Y

#sigmoid函数
def g(z):
    return 1.0/(1+np.exp(-z))

#sigmoid函数的导数
def dgdz(z):
    return np.exp(-z)/((1+np.exp(-z))**2)

#迭代次数
I = 100000

#学习率
alpha = 0.0000001

#网络层数（不算输入层）
L = 5

#数据集大小
m = 10000

#每层的神经元个数（包含输入层）
n = np.array([2,3,5,4,2,1])

#初始化网络参数
W = [1]#W的第一个元素没有意义，也就是说输入层没有参数W，这里随便给一个数值占位
B = [1]#B的第一个元素没有意义，也就是说输入层没有参数B，这里随便给一个数值占位
for i in range(1,L+1):
    W.append(np.random.rand(n[i],n[i-1])*0.001)
    B.append(np.random.rand(n[i],1)*0.001)
    
#初始化训练数据和测试数据
X_train,Y_train = createData(m)
X_test,Y_test = createData(m)

#开始迭代
for i in range(I):
    #前向传播过程初始化
    Z = [1]#Z的第一个元素没有意义，也就是说输入层没有参数Z，这里随便给一个数值占位
    A = [X_train]
    
    #前向传播过程
    for j in range(1,L+1):
        zj = np.dot(W[j],A[j-1]) + B[j]
        aj = g(zj)
        Z.append(zj)
        A.append(aj)
        
    if (i+1)%1000 == 0:
        J = - (np.dot(Y_train,np.log(A[L]).T)+(np.dot((1-Y_train),np.log(1-A[L]).T)))/m
        print("step=%d,cost function=%.14f"%(i+1,J))
    
    #反向传播过程初始化
    dA=[0]*(L+1)
    dA[L] = (-np.dot(Y_train,1.0/A[L].T)+(np.dot((1-Y_train),1.0/(1-A[L]).T)))/m
    
    #反向传播过程
    for j in range(L,0,-1):
        dzj = np.multiply(dA[j], dgdz(Z[j]))
        dwj = np.dot(dzj,A[j-1].T)
        dbj = np.sum(dzj,axis=1,keepdims=True)
        dA[j-1] = np.dot(W[j].T,dzj)
        W[j] = W[j]-alpha*dwj
        B[j] = B[j]-alpha*dbj

#测试过程      
A = [X_test]
for j in range(1,L+1):
    zj = np.dot(W[j],A[j-1]) + B[j]
    aj = g(zj)
    A.append(aj)
Y_hat = (A[L]>0.5).astype(np.int)
rate = 1-np.sum(np.abs(Y_test - Y_hat))/(m)
print('accuracy={0}'.format(rate))

代码运行结果：

最高取得了96%的分类准确率，效果还是可以接受的。做了几次试验后，发现大多数时候可以保证在93%以上的分类准确率。
算法分析：
因为使用的是sigmoid函数，当参数过大时候会出现梯度变小的问题，整个网络收敛速度比较慢。针对这一问题可以考虑使用ReLU激活函数；或者加入batch-normalization层（BN层）（通过某些变换来将数据规格化到0附近，使梯度重新出现）；或使用变化的学习率（即在迭代层数较少时使用较高学习率，随着迭代步数增加减少学习率，这样使前期梯度下降快，后期梯度下降精细）。后期会慢慢更新相关的内容。