最小树形图

转载大佬博客

一、相关定义

定义：设G = (V,E)是一个有向图，它具有下述性质：

1. G中不包含有向环；　
2. 存在一个顶点vi，它不是任何弧的终点，而V中的其它顶点都恰好是唯一的一条弧的终点，则称 G是以vi为根的树形图。

最小树形图就是有向图G = (V, E)中以vi为根的树形图中权值和最小的那一个。

另一种说法：最小树形图，就是给有向带权图一个特殊的点root，求一棵以root为根节点的树使得该树的的总权值最小。

性质：最小树形图基于贪心和缩点的思想。

缩点：将几个点看成一个点，所有连到这几个点的边都视为连到收缩点,所有从这几个点连出的边都视为从收缩点连出

 

二、算法描述

【概述】

为了求一个图的最小树形图，①先求出最短弧集合E0；②如果E0不存在，则图的最小树形图也不存在；③如果E0存在且不具有环，则E0就是最小树形图；④如果E0存在但是存在有向环，则把这个环收缩成一个点u，形成新的图G1，然后对G1继续求其的最小树形图，直到求到图Gi，如果Gi不具有最小树形图，那么此图不存在最小树形图，如果Gi存在最小树形图，那么逐层展开，就得到了原图的最小树形图。

【实现细节】

设根结点为v0，

• （1）求最短弧集合E0

　　从所有以vi(i ≠ 0)为终点的弧中取一条最短的，若对于点i，没有入边，则不存在最小树形图，算法结束；如果能取，则得到由n个点和n-1条边组成的图G的一个子图G'，这个子图的权值一定是最小的，但是不一定是一棵树。

• （2）检查E0

　　若E0没有有向环且不包含收缩点,则计算结束，E0就是图G以v0为根的最小树形图；若E0含有有向环，则转入步骤(3)；若E0没有有向环,但是存在收缩点，转到步骤(4)。

• （3）收缩G中的有向环

　　把G中的环C收缩成点u，对于图G中两端都属于C的边就会被收缩掉，其他弧仍然保留，得到一个新的图G1，G1中以收缩点为终点的弧的长度要变化。变化的规则是：设点v在环C中，且环中指向v的边的权值为w，点v'不在环C中，则对于G中的每一条边<v', v>，在G1中有边<v', u>和其对应，且权值WG1(<v', u>) = WG(<v', v>) - w；对于图G中以环C中的点为起点的边<v', v>，在图G1中有边<u, v'>，则WG1(<u, v'>) = WG(<v', v>)。有一点需要注意,在这里生成的图G1可能存在重边。

　　对于图G和G1：

　　①如果图G1中没有以v0为根的最小树形图，则图G也没有；

　　②如果G1中有一v0为根的最小树形图，则可按照步骤（4）的展开方法得到图G的最小树形图。

所以，应该对于图G1代到(1)中反复求其最小树形图，直到G1的最小树形图u求出。

• （4）展开收缩点

　　假设图G1的最小树形图为T1,那么T1中所有的弧都属于图G的最小树形图T。将G1的一个收缩点u展开成环C，从C中去掉与T1具有相同终点的弧，其他弧都属于T。

【小结】

对最小树形图做个小小的总结：

1：清除自环，自环是不可能存在于任何最小树形图中的；

2：求出每个顶点的的最小入边；

3：判断该图是否存在最小树形图，由 1 可以判定，或者以图中顶点v作为根节点遍历该图就能判断是否存在最小树形图；

4：找环，之后建立新图，缩点后重新标记。

【图示——最小树形图构造流程】

 

 

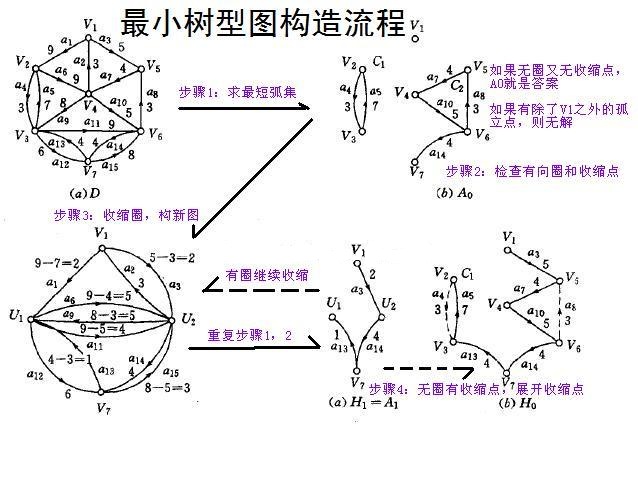
解读：第一幅图为原始图G，首先对于图G求其最短弧集合E0，即第二幅图G1；然后检查E0是满足条件，在这里，可以看到G1具有两个环，那么把这两个环收缩，如第三幅图所示，U1、U2分别为收缩后的点，然后将对应的权值进行更新，起点是环中的点，终点是环外的点，则权值不变。反之，起点是环外的点，终点是环内的点，则权值应该减去E0中指向环内点的权值，形成新的图，如第三幅图，对于其反复求最小树形图，直到不存在最小树形图，或者求得缩点后的图的最小树形图，然后展开就好了，如第六幅图。

如果只要求计算权值的话，则不需要展开，所有环中权值的和加上其他各个点与点之间，或者收缩点和点之间的权值就是总的权值。

三、CODE：

const int inf = 2e9;
const int maxn = 105;
const int maxm = 100050;

int n, m;                   //顶点数，边数  
int in[maxn];               //in[u]记录当前图中指向 u 结点的所有边权中最小的那条边权 
int pre[maxn];              //pre[u]记录最小边权对应的父亲结点 
int used[maxn], id[maxn];   //used是访问标记数组，id[u]是计算出 u 在下一次的新图中的编号 

struct Edge {
    int from, to;
    int dist;
    Edge(int f = 0, int t = 0, int d = 0) :from(f), to(t), dist(d) {}
}edges[maxm];//边集 

// 解决函数

int direct_mst(int root, int V, int E) {        //三个参数分别是根结点，顶点数量，边数量 
    int ans = 0;
         //为每个非根结点选出最小入边 
    while (1) {                           
        for (int i = 0; i < V; ++i) 
            in[i] = inf;
        
        for (int i = 0; i < E; ++i) {
            int u = edges[i].from;
            int v = edges[i].to;
            if (in[v] > edges[i].dist && u != v) {
                in[v] = edges[i].dist;
                pre[v] = u;
            }
        }
        //判断连通性，如有不可达结点说明无解
        
        for (int i = 0; i < V; ++i) {
            if (i == root) continue;
            if (inf == in[i]) return -1;
        }

        //判断有向环是否存在，存在有向环就缩圈
        
        int cnt = 0;                            //生成新图的结点编号
        memset(id, -1, sizeof(id));             // id[u]==-1 表示结点 u 还不属于任何一个自环 
        memset(used, -1, sizeof(used));
        in[root] = 0;
        for (int i = 0; i < V; ++i) {
            ans += in[i];
            int v = i;
            //每个结点不断向上寻找父亲结点，要么找到根结点，要么形成一个自环 
            
            while (used[v] != i && id[v] == -1 && v != root) {
                used[v] = i;
                v = pre[v];
            }
            //当 used[v]==i 的时候代表找到了自环，进行缩点，更新id数组 
            
            if (v != root && id[v] == -1) {
                for (int u = pre[v]; u != v; u = pre[u])
                    id[u] = cnt;
                id[v] = cnt++;
            }
        }

        if (0 == cnt) break;//没有自环说明已经求出最终结果

        //建立新图
        
        //先把不在自环中的点的编号更新  

        for (int i = 0; i < V; i++)
            if (id[i] == -1) id[i] = cnt++;
            
        for (int i = 0; i < E; i++) {
            int u = edges[i].from;
            int v = edges[i].to;
            edges[i].from = id[u];
            edges[i].to = id[v];
            if (id[u] != id[v]) 
                edges[i].dist -= in[v];
            //这里id[u] != id[v]说明  edges[i]这条边原来不在有向环中，
            //如果这条边指向了有向环，那么它的边权就要减少  in[v] 等价于整个环的边权减去in[v]
            //而如果没有指向有向环，说明它与这个有向环毫无关系，那么在之前的寻找自环缩点过
            //程中已经把这条边的权值加上了，所以这里避免重复计算让这条边的权值减小in[v]变为0 
        }
        V = cnt;
        root = id[root];
    }
    return ans;
}