CPK (制程能力指数)

1.CPK（制程能力指数）用于衡量生产过程的稳定性和能力，评估产品规格的一致性。

2.CPK的值是根据具体的产品规格、生产过程数据以及统计分析得出。
 

3.CPK的值越高，表示制程能力越强，产品规格的一致性越好。
 

CPK与不良率（PPM 百万分之一  即每百万件产品中的不良品数）的对照关系

cpk值	不良率
0.67	非常高
1.00	较高
1.33	中等
1.67	较低
2.00	非常低

当CPK值达到1.33或更高时，通常认为制程能力良好，不良率相对较低

具体的CPK值根据产品特性、客户需求和行业标准而异。

关键参数：

 

• $USL$（Upper Specification Limit）：规格上限，即产品规格允许的最大值。
•  $LSL$（Lower Specification Limit）：规格下限，即产品规格允许的最小值。
• $\mu$（Mean）：制程数据的平均值
• $\sigma$（Sigma）：制程数据的标准差
• “\frac{}{}”是数学中表示分数的一种标准方式。具体来说，“\frac{a}{b}”表示a除以b的分数形 式，   其中a是分子，b是分母
•   计算与规格上限的偏差公式： [ \frac{USL - \mu}{3*sigma}   =  [规格上限 减去 平均值] 除以[3乘  标准差]
• 计算与规格下限的偏差公式： [ \frac{\mu - LSL}{3*sigma} = [平均值 减去 规格上限] 除以[3乘  标准差]   

案例

某家汽车制造厂商生产汽车发动机缸套，其长度规格要求为98-102毫米（即LSL=98毫米，USL=102毫米）。估该生产过程的稳定性和能力，厂商从生产线上随机抽取了20个发动机缸套样本进行测量，并计算了样本的平均值和标准偏差。

测量数据

• 样本数量：20个
• 样本平均值（μ）：99.5毫米
• 样本标准偏差（σ）：0.5毫米

• 计算与规格上限的偏差： \frac{102 - 99.5}{3*0.5} = \frac{2.5}{1.5} = 1.67

• 计算与规格下限的偏差： \frac{99.5 - 98}{3*0.5} = \frac{1.5}{1.5} = 1.00

• 取两者中的最小值作为CPK： 1.00

MiniTab软件 计算CPK   

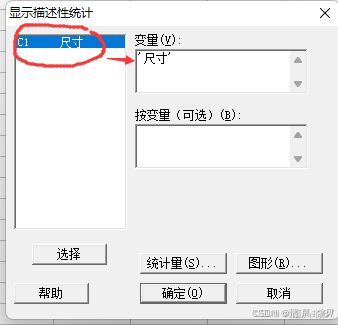
1.打开minitab，把测试获得的数据复制到minitab软件内，数据放在同一列中  填入（尺寸）

数据越多越能真实反映加工能力的水平

 

2. 计算CPK

(1)找到并点击“选择统计”菜单栏，在其下找到“质量工具”选项，并依次选择能力分析、正态选项

填入 对用数据列 和USL 和LSL

cpk 0.26 说明 产品  不良率高     需要改进生产过程的稳定性和能力

 扩展：mintab计算数据标准差和平均值

3.根据上图标准差和平均数计算 USL 和LSL 

• 计算与规格上限的偏差USL：[规格上限 减去 平均值] 除以[3乘  标准差]   

• 计算与规格下限的偏差LSL： [规格下限 减去 平均值] 除以[3乘  标准差]   

MiniTab软件 计算GRR

打开minitab软件，分别录入3组数据：

①10个零部件的编号

②3个操作员名字/编号

③每次测量数据，注意数据一定要录入正确  

4.扩展  如果有多行数据  可以通过（在“数据”菜单下的下拉列表中，选择“堆叠”——“列”选项）把数据合并

依次打开统计→质量工具→量具研究→量具R&R研究（交叉） 

在部件号位置选择“部件”；

操作员位置选择“操作员”；

测量数据位置选择“测量”，

分析方法勾选“方差分析” 

 点击“量具信息”，在对话框中录入相关量具信息，研究时间等，点击“确定”回到上一对话框。

  GRR结果图

标准差的大小反映了测量结果的稳定性，标准差越大，说明数据点与平均值的偏离程度越大，即数据的离散程度越高；反之，标准差越小，说明数据点越接近平均值，数据的离散程度越低

 

项目工作流程

1.接到项目需求、根据项目测量精度选择合适的相机和镜头

2.准备电脑、相机、镜头、光源、打光支架等一套系统

3.如果客户可以提供样品到车间外面，可以在公司实验室打光测试

如果不允许则需要到车间现场打光测试

4.出具打光方案、评估项目风险

  如 测量项目、机台运行过程中车间是否有强烈的震动

     产品是否是在治具中单片测量

     如果在塑料料盘里如何保证焦距一致性

5.测量静态重复性，保证视觉检测方面没有问题

6.和机构设计沟通视觉方案的安装方式和检测CT（检测时间）

7.编写程序和检测算法

8.机台到现场以后调试程序、测量动态重复性，保证设备检测精度没有问题

9.如果是测量机台调试完成，和客户一起做相关性

10.如果是引导机台，测量动态重复性保证找到的贴合点坐标位置准确

11.贴合完成后 做CPK等相关数据，保证机台稳定性没有问题