【大模型系列篇】大模型深度思考新范式：交替「推理-擦除」

木亦汐丫

已于 2025-05-20 09:56:00 修改

阅读量797

点赞数 20

分类专栏：大模型文章标签： CoT 深度思考新范式 PENCIL 交替「推理-擦除」图灵完备大模型

于 2025-05-20 07:00:00 首次发布

本文链接：https://blog.csdn.net/Jackie_vip/article/details/148059616

版权

大模型专栏收录该内容

56 篇文章

订阅专栏

近期的大型语言模型 (LLM) ，例如 OpenAI 的 o1/o3、DeepSeek 的 R1 和 Anthropic 的 Claude 3.7，都表明允许模型在测试时进行更深入、更长时间的思考可以显著提升模型的推理能力。这些深度思维能力背后的核心方法被称为思维链 (CoT) ，即模型迭代生成中间推理步骤并将其附加到当前上下文中，直至得出最终答案。

然而，随着任务变得越来越复杂，解决问题所需的步骤也急剧增加。例如，考虑使用 CoT 解决 NP 难题——假设使用固定大小的 Transformer 作为基础模型，并且 P ≠ NP，推理轨迹将不可避免地跨越指数级步骤。这就引出了一个重要的问题：基于 CoT 的测试时间扩展是否会遇到硬性限制？

不幸的是，很可能是的。对于更艰巨的任务，各种限制都会出现：

思维链不可避免地会超出模型的上下文窗口；
关键信息会被埋没，几乎不可能从众多先前的标记中检索出来；
自注意力机制的复杂性使得生成每个新标记的成本过高。

选择性丢弃信息的想法在计算机科学史上有着深厚的根源，从最早的计算模型到现代系统皆是如此。经典的图灵机会覆盖磁带上的符号，而不是保留所有状态；编程语言通过堆栈帧回收内存，这些堆栈帧会在函数执行完成后自动释放；现代垃圾收集器会持续识别并移除程序不再访问的对象。这些机制不仅仅是效率优化，更是在有限资源内实现复杂计算的关键设计选择。

这一理念也适用于人类的推理。在定理证明中，一旦引理成立，人们就会舍弃其推导细节，同时保留结果；在探索解决问题的方法时，人们只是将无效路径标记为“失败”，而不会保留其完整轨迹。在复杂的推理过程中，人类自然会压缩信息，保留结论，同时舍弃得出结论所需的框架。

大模型深度思考新范式：交替「推理-擦除」

论文：《PENCIL: Long Thoughts with Short Memory》
代码： https://github.com/chr26195/PENCIL

因此，该论文作者提出了 PENCIL，一种新的 LLM 推理范式。与仅生成想法的 CoT 不同，PENCIL 会递归地生成和删除想法，直到得出最终答案。它只保留生成未来想法所需的最小上下文，因此模型可以进行更长时间、更深入的思考，从而利用更短的工作记忆来解决更困难的任务。

CoT 将每步推理串联到上下文中直到给出答案并返回整个序列。
PENCIL 交替执行生成（图中加粗部分）和擦除（图中绿色高亮部分）：模型先写出新的思考过程，再删掉对之后的推理无用片段，只保留对后续的推理过程有用的部分，内部形成一系列隐式思维，最后仅返回最终答案。

模型如何消除思想？

PENCIL的擦除机制借鉴了两种经典思想。首先，源自逻辑中的重写规则和经典的自动定理证明 ，它们不断应用预定义的规则，将复杂的逻辑或算术表达式简化为规范形式，直到得到最终答案。其次，源自函数式编程语言 ，它在调用函数时创建堆栈框架来存储局部变量，并在函数返回时释放相应的内存，自动丢弃不再需要的中间状态。

具体来说，引入三个特殊标记，称为[CALL]，[SEP]和[RETURN]，并使用以下减少规则来实现擦除：

其中 C 代表上下文， T 代表中间想法， A 代表答案。每当生成的序列与左侧的模式完全匹配时，PENCIL 就会触发归约规则，删除想法并将答案合并到上下文中。需要注意的是， C 、 T 和 A 本身可以包含特殊标记，从而支持类似于嵌套函数调用的递归结构——例如， C 可能包含另一个 [CALL] 标记，表示已启动一个新的思考子程序。

如何使用 PENCIL？

PENCIL 的擦除机制能够灵活支撑多种推理模式，例如：

任务分解：使用[CALL]发起子问题，生成中间结果，然后使用[SEP]和[RETURN]合并输出并擦除子问题推理细节；
分支与回溯：使用 [CALL]、[SEP]、[RETURN] 三元组来管理搜索树中的探索分支，在发生冲突或失败时删除无效路径；
摘要与总结：将冗长的推理线索浓缩为简洁的摘要，类似于编程中的尾部递归优化：

其中 T 表示原始复杂的推理过程（或更困难的问题）， T' 表示总结或简化的内容（或等效的、更易处理的问题）。

示例：考虑一个经典的 NP 完全问题：布尔可满足性（SAT）：给定一个布尔公式，判断是否存在一个变量赋值使其成立。这个问题（普遍认为）需要指数级时间 ，但求解空间仅为多项式 ，最简单的方法是遍历深度为 n 的二叉搜索树。

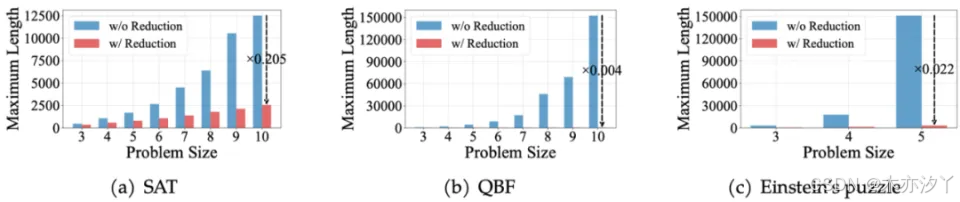
传统的 CoT 会累积中间计算，导致上下文长度与搜索树中的节点数量成正比增长，其时间复杂度为 O(2^n)。相比之下，PENCIL 可以递归分支来尝试对变量进行 True/False 判断，在冲突时回溯并删除该分支内的所有想法。这使得上下文长度与搜索深度成正比，其空间复杂度仅为 O(n)。

如图所示，对比 CoT 无擦除（蓝）与 PENCIL 擦除（红）两种思考模式下的最大上下文长度，随着问题复杂度的增加，PENCIL 实现了显著的空间效率提升，尤其在解决爱因斯坦谜题时，上下文长度从 151,192 个 token 减少到了 3,335 个 token。

训练与实验

CoT 和 PENCIL 在训练过程中的核心区别在于损失函数的计算：

对于 CoT，每个新 token 的损失基于完整的历史上下文；对于 PENCIL，在每次“写入-擦除”迭代之后，模型仅在缩减后的序列上计算新 token 的损失。虽然两者生成的 token 数量相同，但 PENCIL 显著缩短了每个 token 对应的上下文长度，因此效率更高。

另一点值得注意的是，每次缩减之后，共享前缀 C 的 KV 缓存可以直接重用，只有较短部分 A 的缓存需要重新计算。

实验结果

实验重点关注三项本质上难度较高的推理任务：3-SAT（NP-Complete）、QBF（PSPACE-Complete）和爱因斯坦谜题（自然语言推理）。针对每项任务，作者编写了一个生成器来生成包含特殊标记的训练集。针对这些任务，从随机初始化开始训练了一个小型转换器（SAT/QBF 包含 10.6M 个参数；爱因斯坦谜题包含 25.2M 个参数）。

与 CoT 相比，作者发现 PENCIL 能够解决更大规模的推理问题。如下图所示，在 SAT（左）和 QBF（右）任务中，当问题规模较小时，CoT 和 PENCIL 都能完美解决问题；但随着规模的增加，传统 CoT 的准确率显著下降（例如，在 n=10 时，SAT 的准确率仅为 50% 左右），而 PENCIL 则能保持 ≥ 99% 的高精度。这主要是因为 CoT 的上下文序列长度呈指数级爆炸式增长，而 PENCIL 通过动态缩减来避免爆炸式增长。

此外，PENCIL 显著节省了计算资源。如图所示，对于 QBF（n=3-6）任务，我们比较了相同 FLOP 预算下 CoT（蓝色）和 PENCIL（红色）的收敛速度。PENCIL 很快达到了 100% 的准确率，而 CoT 由于上下文长度不断增加，需要更多 FLOP 才能接近最优值。随着问题规模的增加，两者之间的差距更加明显。

我们进一步思考了一个非常困难的逻辑推理问题：爱因斯坦谜题。每个问题包含 5 栋房屋和居住在其中的人的 5 个属性类别——颜色、国籍、饮料、香烟和宠物（例如，红色/绿色/蓝色、英国/德国/瑞典、鸟/狗/鱼等）。给定诸如“绿色房子就在鸟主人家旁边”和“狗主人住在红色房子里”之类的线索，任务是推断“谁是鱼的主人？”这个问题对现有的 LLM 提出了极大的挑战：即使是 GPT-4 也难以解决。下图显示了一个简化版本，其中只有 3 栋房屋和 3 个属性类别：

如下所示，对于这个连大型模型都难以解决的问题，PENCIL 仅使用一个 25.2M 参数的小模型就达到了 97% 的准确率，而传统的 CoT 只能达到 25% 的准确率（接近随机猜测）。

理论：通用高效计算

理论表达能力的角度证明了 PENCIL 相较于传统 CoT 的根本优势：PENCIL 是图灵完备的，具有最优的空间复杂度，因此可以高效地解决任意可计算任务。而这对于 CoT 来说根本不可能实现！

步骤 1：使用 CoT 编码图灵机转换如上图左侧所示，我们将每个图灵机状态转换编码为一个 token，其中包含“新状态”、“书写符号”和“头部移动方向”三元组。模型可以利用自注意力机制计算当前头部位置并确定该位置的符号。无需约简，此过程即可生成 T 个 token，其上下文长度为 O(T)。

步骤 2：交替“模拟-总结” PENCIL 通过交替实现空间/时间最优：

模拟：不断生成图灵机状态转换标记，模拟多个计算步骤；
总结：当新标记超过所需空间的两倍时，使用 S 个标记总结计算结果。然后，约简规则会丢弃之前的想法，只保留最新的图灵机状态以供下一轮使用。

通过这种策略将总令牌生成保持在 O(T)，同时将上下文长度限制为 O(S)。

步骤 3：Transformer 实现为了证明这个过程可以用 Transformer 实现，我们开发了全访问序列处理 (FASP) 编程语言，并证明用 FASP 编写的任何算法都可以用固定大小的 Transformer 实现。在 FASP 程序中，每个变量对应一个 Transformer 子模块，每行代码通过预定义函数将现有变量转换为新变量，这相当于基于子模块构建一个更复杂的 Transformer。程序返回的变量就是编码该算法所需的 Transformer。我们编写了一个实现“模拟-汇总”操作的 FASP 程序，这意味着存在一个可以执行相同功能的恒定大小的 Transformer。

结论

论文作者提出了一种新的推理范式 PENCIL，它在生成和擦除之间交替，使模型能够更深入地思考以解决更复杂的问题。理论上证明了 PENCIL 实现了图灵完备性，并具有最优的时间和空间效率，因此可以高效地解决任何可计算问题。展望未来，一个有希望的方向是对 LLM 进行微调，以融入 PENCIL 内存高效的推理能力。作者希望这些发现能够启发人们从计算理论的角度重新审视当前的推理模型。