分支限界法----旅行售货员问题

一、问题描述

某售货员要到若干城市去推销商品，已知各城市之间的路程(或旅费)。他要选定一条从驻地出发，经过每个城市一次，最后回到驻地的路线，使总的路程(或总旅费)最小。

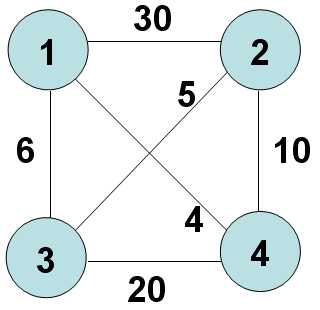
        如下图：1，2，3，4 四个城市及其路线费用图，任意两个城市之间不一定都有路可达。

 

      

二、问题理解

      1.分支限界法利用的是广度优先搜索和最优值策略。

      2.利用二维数组保存图信息City_Graph[MAX_SIZE][MAX_SIZE]

         其中City_Graph[i][j]的值代表的是城市i与城市j之间的路径费用

         一旦一个城市没有通向另外城市的路，则不可能有回路，不用再找下去了

      3. 我们任意选择一个城市，作为出发点。（因为最后都是一个回路，无所谓从哪出发）

 

      下面是关键思路：

       想象一下，我们就是旅行员，假定从城市1出发，根据广度优先搜索的思路，我们要把从城市1能到达的下一个城市，都要作为一种路径走一下试试。

       可是程序里面怎么实现这种“试试”呢？

       利用一种数据结构，保存我们每走一步后，当前的一些状态参数，如，我们已经走过的城市数目（这样就知道，我们有没有走完，比如上图，当我们走了四个城市之后，无论从第四个城市是否能回到起点城市，都就意味着我们走完了，只是这条路径合不合约束以及能不能得到最优解的问题）。这里把，这种数据结构成为结点。这就需要另一个数据结构，保存我们每次试出来的路径，这就是堆。

       数据结构定义如下：

Node{ int s; //结点深度，即当前走过了几个城市 int x[MAX_SIZE]; //保存走到这个结点时的路径信息 } MiniHeap{ //保存所有结点并提供一些结点的操作 } 

 

 

       a.我们刚开始的时候不知道最总能得到的路径是什么，所以我们，就认为按照城市编号的次序走一遍。于是有了第一个结点0，放入堆             中。 相当于来到了城市1(可以是所有城市中的任意一个，这里姑且设为图中城市1)。

       b.从城市1，出发，发现有三条路可走，分别走一下，这样就产生了三个结点，都放入堆中。

          结点1 数据为：x[1 2 3 4]，深度为s=1（深度为0表示在城市1还没有开始走），这说明，结点1是从城市1走来，走过了1个城                                      市，当前停在城市2，后面的城市3 和城市4都还没有走，但是具体是不是就按照3.4的顺序走，这个不一定。

          结点2 数据为：x[1 3 2 4]，深度为s=1，表示，从城市1走来，走过了1个城市，当前停在了城市3，后面2.4城市还没走

          结点3 数据为：x[1 4 3 2]，深度为s=1，表示，从城市1走来，走过了1个城市，当前停在了城市4，后面3.2城市还没有走

       c. 从堆中取一个结点，看看这个结点是不是走完了的，也就是要看看它的深度是不是3，是的话，说明走完了，看看是不是能回到起                点，如果可以而且费用少于先前得到最优的费用，就把当前的解作为最优解。

           如果没有走完，就继续把这条路走下去。

 

以上就是简单的想法，而实际的程序中，堆还需要提供对结点的优先权排序的支持。而当前结点在往下一个城市走时，也是需要约束和限界函数，这些书上讲的很清楚，不懂，就翻翻书。

有点要提出来说说的就是结点优先权和限界函数时都用到了一个最小出边和，就相当于把所有城市最便宜的一条路（边）费用加起来的值。

 

 

下面是代码

#include <stdio.h> #include <istream> using namespace std; //---------------------宏定义------------------------------------------ #define MAX_CITY_NUMBER 10 //城市最大数目 #define MAX_COST 10000000 //两个城市之间费用的最大值 //---------------------全局变量---------------------------------------- int City_Graph[MAX_CITY_NUMBER][MAX_CITY_NUMBER]; //表示城市间边权重的数组 int City_Size; //表示实际输入的城市数目 int Best_Cost; //最小费用 int Best_Cost_Path[MAX_CITY_NUMBER]; //最小费用时的路径 //------------------------定义结点--------------------------------------- typedef struct Node{ int lcost; //优先级 int cc; //当前费用 int rcost; //剩余所有结点的最小出边费用的和 int s; //当前结点的深度，也就是它在解数组中的索引位置 int x[MAX_CITY_NUMBER]; //当前结点对应的路径 struct Node* pNext; //指向下一个结点 }Node; //---------------------定义堆和相关对操作-------------------------------- typedef struct MiniHeap{ Node* pHead; //堆的头 }MiniHeap; //初始化 void InitMiniHeap(MiniHeap* pMiniHeap){ pMiniHeap->pHead = new Node; pMiniHeap->pHead->pNext = NULL; } //入堆 void put(MiniHeap* pMiniHeap,Node node){ Node* next; Node* pre; Node* pinnode = new Node; //将传进来的结点信息copy一份保存 //这样在函数外部对node的修改就不会影响到堆了 pinnode->cc = node.cc; pinnode->lcost = node.lcost; pinnode->pNext = node.pNext; pinnode->rcost = node.rcost; pinnode->s = node.s; pinnode->pNext = NULL; for(int k=0;k<City_Size;k++){ pinnode->x[k] = node.x[k]; } pre = pMiniHeap->pHead; next = pMiniHeap->pHead->pNext; if(next == NULL){ pMiniHeap->pHead->pNext = pinnode; } else{ while(next != NULL){ if((next->lcost) > (pinnode->lcost)){ //发现一个优先级大的，则置于其前面 pinnode->pNext = pre->pNext; pre->pNext = pinnode; break; //跳出 } pre = next; next = next->pNext; } pre->pNext = pinnode; //放在末尾 } } //出堆 Node* RemoveMiniHeap(MiniHeap* pMiniHeap){ Node* pnode = NULL; if(pMiniHeap->pHead->pNext != NULL){ pnode = pMiniHeap->pHead->pNext; pMiniHeap->pHead->pNext = pMiniHeap->pHead->pNext->pNext; } return pnode; } //---------------------分支限界法找最优解-------------------------------- void Traveler(){ int i,j; int temp_x[MAX_CITY_NUMBER]; Node* pNode = NULL; int miniSum; //所有结点最小出边的费用和 int miniOut[MAX_CITY_NUMBER]; //保存每个结点的最小出边的索引 MiniHeap* heap = new MiniHeap; //分配堆 InitMiniHeap(heap); //初始化堆 miniSum = 0; for (i=0;i<City_Size;i++){ miniOut[i] = MAX_COST; //初始化时每一个结点都不可达 for(j=0;j<City_Size;j++){ if (City_Graph[i][j]>0 && City_Graph[i][j]<miniOut[i]){ //从i到j可达，且更小 miniOut[i] = City_Graph[i][j]; } } if (miniOut[i] == MAX_COST){// i 城市没有出边 Best_Cost = -1; return ; } miniSum += miniOut[i]; } for(i=0;i<City_Size;i++){ //初始化的最优路径就是把所有结点依次走一遍 Best_Cost_Path[i] = i; } Best_Cost = MAX_COST; //初始化的最优费用是一个很大的数 pNode = new Node; //初始化第一个结点并入堆 pNode->lcost = 0; //当前结点的优先权为0 也就是最优 pNode->cc = 0; //当前费用为0（还没有开始旅行） pNode->rcost = miniSum; //剩余所有结点的最小出边费用和就是初始化的miniSum pNode->s = 0; //层次为0 pNode->pNext = NULL; for(int k=0;k<City_Size;k++){ pNode->x[k] = Best_Cost_Path[k]; //第一个结点所保存的路径也就是初始化的路径 } put(heap,*pNode); //入堆 while(pNode != NULL && (pNode->s) < City_Size-1){ //堆不空 不是叶子 for(int k=0;k<City_Size;k++){ Best_Cost_Path[k] = pNode->x[k] ; //将最优路径置换为当前结点本身所保存的 } /* * * pNode 结点保存的路径中的含有这条路径上所有结点的索引 * * x路径中保存的这一层结点的编号就是x[City_Size-2] * * 下一层结点的编号就是x[City_Size-1] */ if ((pNode->s) == City_Size-2){ //是叶子的父亲 int edge1 = City_Graph[(pNode->x)[City_Size-2]][(pNode->x)[City_Size-1]]; int edge2 = City_Graph[(pNode->x)[City_Size-1]][(pNode->x)[0]]; if(edge1 >= 0 && edge2 >= 0 && (pNode->cc+edge1+edge2) < Best_Cost){ //edge1 -1 表示不可达 //叶子可达起点费用更低 Best_Cost = pNode->cc + edge1+edge2; pNode->cc = Best_Cost; pNode->lcost = Best_Cost; //优先权为 Best_Cost pNode->s++; //到达叶子层 } } else{ //内部结点 for (i=pNode->s;i<City_Size;i++){ //从当前层到叶子层 if(City_Graph[pNode->x[pNode->s]][pNode->x[i]] >= 0){ //可达 //pNode的层数就是它在最优路径中的位置 int temp_cc = pNode->cc+City_Graph[pNode->x[pNode->s]][pNode->x[i]]; int temp_rcost = pNode->rcost-miniOut[pNode->x[pNode->s]]; //下一个结点的剩余最小出边费用和 //等于当前结点的rcost减去当前这个结点的最小出边费用 if (temp_cc+temp_rcost<Best_Cost){ //下一个结点的最小出边费用和小于当前的最优解，说明可能存在更优解 for (j=0;j<City_Size;j++){ //完全copy路径，以便下面修改 temp_x[j]=Best_Cost_Path[j]; } temp_x[pNode->x[pNode->s+1]] = Best_Cost_Path[i]; //将当前结点的编号放入路径的深度为s+1的地方 temp_x[i] = Best_Cost_Path[pNode->s+1]; //?????????????? //将原路//径中的深度为s+1的结点编号放入当前路径的 //相当于将原路径中的的深度为i的结点与深度W为s+1的结点交换 Node* pNextNode = new Node; pNextNode->cc = temp_cc; pNextNode->lcost = temp_cc+temp_rcost; pNextNode->rcost = temp_rcost; pNextNode->s = pNode->s+1; pNextNode->pNext = NULL; for(int k=0;k<City_Size;k++){ pNextNode->x[k] = temp_x[k]; } put(heap,*pNextNode); delete pNextNode; } } } } pNode = RemoveMiniHeap(heap); } } int main(){ int i,j; scanf("%d",&City_Size); for(i=0;i<City_Size;i++){ for(j=0;j<City_Size;j++){ scanf("%d",&City_Graph[i][j]); } } Traveler(); printf("%d/n",Best_Cost); return 1; }