历时两月，终拿字节跳动offer，算法面试题分享「带答案」

本文转载自：历时两月，终拿字节跳动offer，算法面试题分享「带答案」

---

一. 最小生成树算法

• 连通图：在无向图G中，若从顶点i到顶点j有路径，则称顶点i和顶点j是连通的。若图G中任意两个顶点都连通，则称G为连通图。
• 生成树：一个连通图的生成树是该连通图的一个极小连通子图，它含有全部顶点，但只有构成一个数的(n-1)条边。
• 最小生成树：对于一个带权连通无向图G中的不同生成树，各树的边上的 权值之和最小。构造最小生成树的准则有三条：
  • 必须只使用该图中的边来构造最小生成树。
  • 必须使用且仅使用(n-1)条边来连接图中的n个顶点。
  • 不能使用产生回路的边。

1. Prim算法

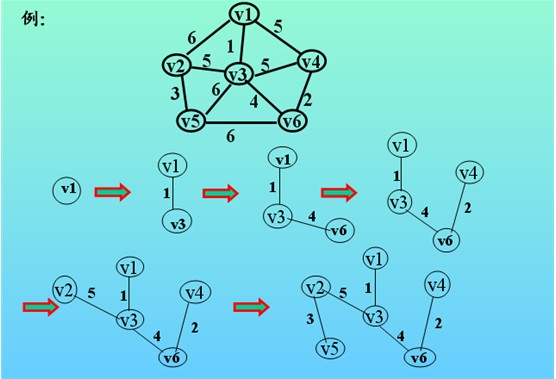
假设G=(V,E)是一个具有n个顶点的带权连通无向图，T(U,TE)是G的最小生成树，其中U是T的顶点集，TE是T的边集，则由G构造从起始顶点v出发的最小生成树T的步骤为：

• 初始化U={v}，以v到其他顶点的所有边为候选边(U中所有点到其他顶点的边)。
• 重复以下步骤(n-1)次，使得其他(n-1)个顶点被加入到U中。
  • 从候选边中挑选权值最小的边加入TE，设该边在V-U(这里是集合减)中的顶点是k，将k加入U中。
  • 考察当前V-U中的所有顶点j，修改候选边，若边(k,j)的权值小于原来和顶点j关联的候选边，则用(k,j)取代后者作为候选边。

2. Kruskal算法

假设G=(V,E)是一个具有n个顶点的带权连通无向图，T(U,TE)是G的最小生成树，其中U是T的顶点集，TE是T的边集，则由G构造从起始顶点v出发的最小生成树T的步骤为：

• 置U的初始值等于V(即包含G中的全部顶点)，TE的初始值为空
• 将图G中的边按权值从小到大的顺序依次选取，若选取的边未使生成树T形成回路，则加入TE，否则放弃，知道TE中包含(n-1)条边为止。

二. 最短路径算法

1. Dijkstra —— 贪心算法

从一个顶点到其余顶点的最短路径

设G=(V,E)是一个带权有向图，把图中顶点集合V分成两组，第1组为已求出最短路径的顶点（用S表示，初始时S只有一个源点，以后每求得一条最短路径v,…k，就将k加到集合S中，直到全部顶点都加入S）。第2组为其余未确定最短路径的顶点集合（用U表示），按最短路径长度的递增次序把第2组的顶点加入S中。

步骤：

1. 初始时，S只包含源点，即S={v}，顶点v到自己的距离为0。U包含除v外的其他顶点，v到U中顶点i的距离为边上的权。
2. 从U中选取一个顶点u，顶点v到u的距离最小，然后把顶点u加入S中。
3. 以顶点u为新考虑的中间点，修改v到U中各个点的距离。
4. 重复以上步骤知道S包含所有顶点。

2. Floyd —— 动态规划

Floyd 算法是解决任意两点间的最短路径的一种算法，可以正确处理有向图或负权（但不可存在负权回路）的最短路径问题。该算法的时间复杂度为$$O(N^{3})$$，空间复杂度为 $$O(N^{2})$$

设$$D_{i,j,k}$$为从$$i$$到$$j$$的只以$$(1..k)$$集合中的节点为中间节点的最短路径的长度。

$$ D{i,j,k}=\begin{cases} D{i,j,k-1} &最短路径不经过k D{i,k,k-1}+D{k,j,k-1} &最短路径经过k \end{cases} $$

因此，$$D{i,j,k}=min(D{i,k,k-1}+D{k,j,k-1},D{i,j,k-1})$$。伪代码描述如下：

// let dist be a |V| × |V| array of minimum distances initialized to ∞ (infinity)
for each vertex v
    dist[v][v] ← 0
 for each edge (u,v)
    dist[u][v] ← w(u,v)  // the weight of the edge (u,v)
for k from 1 to |V|