目录
深度优先遍历(Depth First Search)的主要思想是:
图(Graph)
G由顶点集合V(G)和边集合E(G)构成。顶点的编号为0~n-1。通过编号唯一确定一个顶点。
在图G中,如果代表边的顶点对是无序的,则称G为无向图。用圆括号序偶表示无向边。(0,1)
如果表示边的顶点对是有序的,则称G为有向图。用尖括号序偶表示有向边。<0,1>(通俗点讲有箭头的是有向图,无箭头的是无向图)

无向图:表示形式, 有向图:表示形式,
图:G1=(V1,E1); 图:G2=(V2,E2);
顶点:V1={0,1,2,3,4}; 顶点:V1={0,1,2,3,4};
边:E1={(0,1),(0,3),(0,4),(1,2),(1,3),(2,3),(2,4),(3,4)}; 边:E2={<0,1>,<0,3>,<1,2>,<1,3>,<2,3>,<2,4>,<4,3>,<4,0>};
完全无向图:
对于无向图,若图中顶点数为n ,用e表示边的数目,则e [0,n(n-1)/2] 。具有n(n-1)/2条边的无向图称为完全无向图
另一种说法:即图中任意两个不同的顶点间都有一条无向边,这样的无向图称为完全无向图。
完全有向图:
对于有向图,若图中顶点数为n ,用e表示弧的数目,则e[0,n(n-1)] 。具有n(n-1)条边的有向图称为完全有向图。(是完全无向图边的2 倍)
另一种说法:即图中任意两个不同的顶点间都有一条弧,这样的有向图称为完全有向图。
有很少边或弧的图(e<n㏒n)的图称为稀疏图,反之称为稠密图。
权(Weight):
与图的边和弧相关的数。权可以表示从一个顶点到另一个顶点的距离或耗费。
子图和生成子图:
设有图G1=(V1,E1)和G2=(V2,E2),
若V2<V1且E2<E1 ,则称图G2是G1的子图;(顶点和边都不同)
若V2=V1且E2<E1,则称图G2是G1的一个生成子图。(顶点相同,边不同)
邻接点:
对于无向图G=(V,E),若边(v,w)<E,则称顶点v和w 互为邻接点,即v和w相邻接。
边(v,w)依附(incident)于顶点v和w ,或者说顶点v和w “相关联” 。
度:
与顶点vi相关的边的条数称作顶点vi的度(degree),记为TD(vi)。
在无向图中,所有顶点度的和是图中边的2倍。
对有向图G=(V,E),若vi V ,图G中以vi作为起点的有向边(弧)的数目称为顶点vi的出度(Outdegree),记为OD(vi) ;
以vi作为终点的有向边(弧)的数目称为顶点vi的入度(Indegree),记为ID(vi) 。
顶点vi的出度与入度之和称为vi的度,记为TD(vi) 。即 TD(vi)=OD(vi)+ID(vi)(有向图中度=出度+入度)
生成树、生成森林:
一个连通图(无向图)的生成树是一个极小连通子图,它含有图中全部n个顶点和只有足以构成一棵树的n-1条边,称为图的生成树。


关于无向图的生成树的几个结论:
◆ 一棵有n个顶点的生成树有且仅有n-1条边;
◆ 如果一个图有n个顶点和小于n-1条边,则是非连通图;
◆如果多于n-1条边,则一定有环;
◆有n-1条边的图不一定是生成树。
网:
每个边(或弧)都附加一个权值的图,称为带权图。带权的连通图(包括弱连通的有向图)称为网或网络。
有向图的生成森林是这样一个子图,由若干棵有向树组成,含有图中全部顶点。


图的存储结构:
1:邻接矩阵存储:
G的邻接矩阵A是n阶方阵,其定义如下:
(1)如果G是无向图,则: A[i][j]=1:若(i,j)∈E(G) 0:其他
(2)如果G是有向图,则: A[i][j]=1:若<i,j>∈E(G) 0:其他
(3)如果G是带权无向图,则: A[i][j]= wij :若i≠j且(i,j)∈E(G) 0:i=j ∞:其他
(4)如果G是带权有向图,则: A[i][j]= wij :若i≠j且<i,j>∈E(G) 0:i=j ∞:其他
 在无向图中,若<v,w>E(G) ,有<w,v>E(G) ,即E(G)是对称——解释
在无向图中,若<v,w>E(G) ,有<w,v>E(G) ,即E(G)是对称——解释
十字链表的画法
基本概念
十字链表(Orthogonal List)是有向图的另一种链式存储结构。该结构可以看成是将有向图的邻接表和逆邻接表结合起来得到的。
(画的时候最好写出入弧出弧,弧头弧尾,同弧头同弧尾)
- 入弧和出弧:入弧表示图中发出箭头的顶点,出弧表示箭头指向的顶点。
- 弧头和弧尾:弧尾表示图中发出箭头的顶点,弧头表示箭头指向的顶点。
- 同弧头和同弧尾:同弧头,弧头相同弧尾不同;同弧尾,弧头不同互为相同
深度优先遍历
深度优先遍历(Depth First Search)的主要思想是:
1、首先以一个未被访问过的顶点作为起始顶点,沿当前顶点的边走到未访问过的顶点;
2、当没有未访问过的顶点时,则回到上一个顶点,继续试探别的顶点,直至所有的顶点都被访问过。
在此我想用一句话来形容 “不到南墙不回头”。
1.1 无向图的深度优先遍历图解
以下"无向图"为例:
对上无向图进行深度优先遍历,从A开始:
第1步:访问A。
第2步:访问B(A的邻接点)。 在第1步访问A之后,接下来应该访问的是A的邻接点,即"B,D,F"中的一个。但在本文的实现中,顶点ABCDEFGH是按照顺序存储,B在"D和F"的前面,因此,先访问B。
第3步:访问G(B的邻接点)。 和B相连只有"G"(A已经访问过了)
第4步:访问E(G的邻接点)。 在第3步访问了B的邻接点G之后,接下来应该访问G的邻接点,即"E和H"中一个(B已经被访问过,就不算在内)。而由于E在H之前,先访问E。
第5步:访问C(E的邻接点)。 和E相连只有"C"(G已经访问过了)。
第6步:访问D(C的邻接点)。
第7步:访问H。因为D没有未被访问的邻接点;因此,一直回溯到访问G的另一个邻接点H。
第8步:访问(H的邻接点)F。
因此访问顺序是:A -> B -> G -> E -> C -> D -> H -> F
1.2 有向图的深度优先遍历
有向图的深度优先遍历图解:
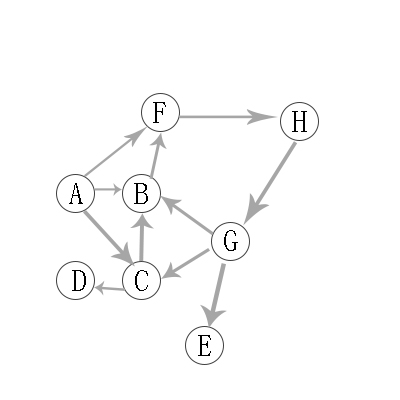
对上有向图进行深度优先遍历,从A开始:
第1步:访问A。
第2步:访问(A的出度对应的字母)B。 在第1步访问A之后,接下来应该访问的是A的出度对应字母,即"B,C,F"中的一个。但在本文的实现中,顶点ABCDEFGH是按照顺序存储,B在"C和F"的前面,因此,先访问B。
第3步:访问(B的出度对应的字母)F。 B的出度对应字母只有F。
第4步:访问H(F的出度对应的字母)。 F的出度对应字母只有H。
第5步:访问(H的出度对应的字母)G。
第6步:访问(G的出度对应字母)E。 在第5步访问G之后,接下来应该访问的是G的出度对应字母,即"B,C,E"中的一个。但在本文的实现中,顶点B已经访问了,由于C在E前面,所以先访问C。
第7步:访问(C的出度对应的字母)D。
第8步:访问(C的出度对应字母)D。 在第7步访问C之后,接下来应该访问的是C的出度对应字母,即"B,D"中的一个。但在本文的实现中,顶点B已经访问了,所以访问D。
第9步:访问E。D无出度,所以一直回溯到G对应的另一个出度E。
因此访问顺序是:A -> B -> F -> H -> G -> C -> D -> E
图的深度优先遍历(DFS)和广度优先遍历(BFS)算法分析 - Hi,Bro - 博客园
广度优先遍历
基础概念及图解
概念:
广度优先遍历算法是图的另一种基本遍历算法,其基本思想是尽最大程度辐射能够覆盖的节点,并对其进行访问。
以迷宫为例,广度优先搜索则可以想象成一组人一起朝不同的方向走迷宫,当出现新的未走过的路的时候,可以理解成一个人有分身术,继续从不同的方向走,,当相遇的时候则是合二为一
自我理解:
正如老师上课所说的,广度优先遍历就像在平静的湖面丢入一块石头,荡起的波纹,从离起始点最近的先开始遍历,同样距离的前后顺序可以交换,如果有环状结构,那遍历过的,就可以跳过,不用重复遍历。
例子解析
例子1:
1.从起点0开始遍历
2.从其邻接表得到所有的邻接节点,把这三个节点都进行标记,表示已经访问过了
3.从0的邻接表的第一个顶点2开始寻找新的叉路
4.查询顶点2的邻接表,并将其所有的邻接节点都标记为已访问
5.继续从顶点0的邻接表的第二个节点,也就是顶点1,遍历从顶点1开始
6.查询顶点1的邻接表的所有邻接节点,也就是顶点0和顶点2,发现这两个顶点都被访问过了,顶点1返回
7.从顶点0的下一个邻接节点,也就是顶点5,开始遍历
8.查询顶点5的邻接节点,发现其邻接节点3和0都被访问过了,顶点5返回
9.继续从2的下一个邻接节点3开始遍历
10.寻找顶点3的邻接节点,发现都被访问过了,顶点3返回
11.继续寻找顶点2的下一个邻接节点4,发现4的所有邻接节点都被访问过了,顶点4返回
12.顶点2的所有邻接节点都放过了,顶点2返回,遍历结束











普里姆算法(Prim算法)求最小生成树
通过前面的学习,对于含有 n 个顶点的连通图来说可能包含有多种生成树,例如图 1 所示:
图 1 连通图的生成树
图 1 中的连通图和它相对应的生成树,可以用于解决实际生活中的问题:假设A、B、C 和 D 为 4 座城市,为了方便生产生活,要为这 4 座城市建立通信。对于 4 个城市来讲,本着节约经费的原则,只需要建立 3 个通信线路即可,就如图 1(b)中的任意一种方式。
在具体选择采用(b)中哪一种方式时,需要综合考虑城市之间间隔的距离,建设通信线路的难度等各种因素,将这些因素综合起来用一个数值表示,当作这条线路的权值。
图 2 无向网
假设通过综合分析,城市之间的权值如图 2(a)所示,对于(b)的方案中,选择权值总和为 7 的两种方案最节约经费。
这就是本节要讨论的最小生成树的问题,简单得理解就是给定一个带有权值的连通图(连通网),如何从众多的生成树中筛选出权值总和最小的生成树,即为该图的最小生成树。
给定一个连通网,求最小生成树的方法有:普里姆(Prim)算法和克鲁斯卡尔(Kruskal)算法。
普里姆算法
普里姆算法在找最小生成树时,将顶点分为两类,一类是在查找的过程中已经包含在树中的(假设为 A 类),剩下的是另一类(假设为 B 类)。
对于给定的连通网,起始状态全部顶点都归为 B 类。在找最小生成树时,选定任意一个顶点作为起始点,并将之从 B 类移至 A 类;然后找出 B 类中到 A 类中的顶点之间权值最小的顶点,将之从 B 类移至 A 类,如此重复,直到 B 类中没有顶点为止。所走过的顶点和边就是该连通图的最小生成树。
例如,通过普里姆算法查找图 2(a)的最小生成树的步骤为:
假如从顶点A出发,顶点 B、C、D 到顶点 A 的权值分别为 2、4、2,所以,对于顶点 A 来说,顶点 B 和顶点 D 到 A 的权值最小,假设先找到的顶点 B:
继续分析顶点 C 和 D,顶点 C 到 B 的权值为 3,到 A 的权值为 4;顶点 D 到 A 的权值为 2,到 B 的权值为无穷大(如果之间没有直接通路,设定权值为无穷大)。所以顶点 D 到 A 的权值最小:
最后,只剩下顶点 C,到 A 的权值为 4,到 B 的权值和到 D 的权值一样大,为 3。所以该连通图有两个最小生成树:
狄克斯特拉算法:
这个人讲的还不错:
Dijkstra(迪杰斯特拉)算法理解_哔哩哔哩_bilibili
1.定义:
广度优先算法可以找出段数最少的路径,但是对于路径上带权重的图,想要找出最快的路径,则需要使用狄克斯特拉算法。
2.原理
为了说明狄克斯特拉算法的原理,使用换钢琴的的例子来做说明.
假设Rama想拿自己的乐谱换架钢琴:
Alex说:“这是我最喜欢的乐队Destroyer的海报,我愿意拿它换你的乐谱。
如果你再加5美元,还可拿乐谱换我这张稀有的Rick Astley黑胶唱片。”
Amy说:“哇,我听说这张黑胶唱片里有首非常好听的歌曲,我愿意拿我的吉他或架子鼓换这张海报或黑胶唱片。
Beethoven惊呼:“我一直想要吉他,我愿意拿我的钢琴换Amy的吉他或架子鼓。”
商品兑换的关系如下:

现在需要确定,Rama如何才能以最少的钱换到他想要的钢琴。
狄克斯特拉算法解决问题的思路主要包括以下四步:
找出最便宜的节点,即可用最便宜的价格可前往的节点。
对于该节点的邻居,检查是否有前往它们的更短路径,如果有,就更新其开销。
重复这个过程,直到对图中的每个节点都这样做了。
计算最终路径
A:乐谱,B:唱片,C:海报,D:吉他,E:架子鼓,F:钢琴

在举例一下:巩固一下

拓扑排序:
https://blog.csdn.net/qq_38984851/article/details/82844186
1、定义
对一个有向无环图(Directed Acyclic Graph简称DAG) G进行拓扑排序,是将G中所有顶点排成一个线性序列,使得图中任意一对顶点u和v,若边(u,v)∈E(G),则u在线性序列中出现在v之前。通常,这样的线性序列称为满足拓扑次序(Topological Order)的序列,简称拓扑序列。简单的说,由某个集合上的一个偏序得到该集合上的一个全序,这个操作称之为拓扑排序。
在AOV网中,若不存在回路,则所有活动可排列成一个线性序列,使得每个活动的所有前驱活动都排在该活动的前面,我们把此序列叫做拓扑序列(Topological order),由AOV网构造拓扑序列的过程叫做拓扑排序(Topological sort)。AOV网的拓扑序列不是唯一的,满足上述定义的任一线性序列都称作它的拓扑序列。
2、拓扑排序的实现步骤
在有向图中选一个没有前驱的顶点并且输出
从图中删除该顶点和所有以它为尾的弧(白话就是:删除所有和它有关的边)
重复上述两步,直至所有顶点输出,或者当前图中不存在无前驱的顶点为止,后者代表我们的有向图是有环的,因此,也可以通过拓扑排序来判断一个图是否有环。
3、拓扑排序示例手动实现
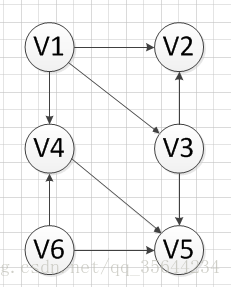
如果我们有如下的一个有向无环图,我们需要对这个图的顶点进行拓扑排序,过程如下:
首先,我们发现V6和v1是没有前驱的,所以我们就随机选去一个输出,我们先输出V6,删除和V6有关的边,得到如下图结果:
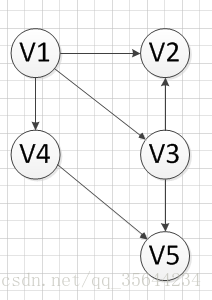
然后,我们继续寻找没有前驱的顶点,发现V1没有前驱,所以输出V1,删除和V1有关的边,得到下图的结果:
然后,我们又发现V4和V3都是没有前驱的,那么我们就随机选取一个顶点输出(具体看你实现的算法和图存储结构),我们输出V4,得到如下图结果:
然后,我们输出没有前驱的顶点V3,得到如下结果:
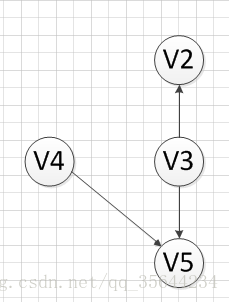
然后,我们分别输出V5和V2,最后全部顶点输出完成,该图的一个拓扑序列为:
v6–>v1—->v4—>v3—>v5—>v2
过程简述:
从 DAG 图中选择一个 没有前驱(即入度为0)的顶点并输出。
从图中删除该顶点和所有以它为起点的有向边。
重复 1 和 2 直到当前的 DAG 图为空或当前图中不存在无前驱的顶点为止。若当前图中不存在无前驱的顶点说明有向图中必存在环。
关键路径:
图——关键路径_fu_jian_ping的博客-CSDN博客_关键路径
从AOE网中源点到汇点的最长路径,具有最大长度的路径叫关键路径。
关键路径是由关键活动构成的,关键路径可能不唯一。
AOE网示例图:
AOE网:在一个表示工程的带权有向图中,用顶点表示事件(如V0),用有向边表示活动(如<v0,v1> = a1),边上的权值表示活动的持续时间,称这样的有向图为边表示的活动的网,简称AOE网(activity on edge network)
源点:
在AOE网中,没有入边的顶点称为源点;如顶点V0
终点:
在AOE网中,没有出边的顶点称为终点;如顶点V3
AOE网的性质:
【1】只有在进入某顶点的活动都已经结束,该顶点所代表的事件才发生;
例如:a1和a2活动都结束了,顶点V2所代表的事件才会发生。
【2】只有在某顶点所代表的事件发生后,从该顶点出发的各活动才开始;
例如:只有顶点V1所代表的事件结束之后,活动a2和a4才会开始。
在AOE网中,所有活动都完成才能到达终点,因此完成整个工程所必须花费的时间(即最短工期)应该为源点到终点的最大路径长度。具有最大路径长度的路径称为关键路径。关键路径上的活动称为关键活动:
事件的最早发生时间:ve[k]
根据AOE网的性质,只有进入Vk的所有活动<Vj, Vk>都结束,Vk代表的事件才能发生,而活动<Vj, Vk>的最早结束时间为ve[j]+len<Vj, Vk>。所以,计算Vk的最早发生时间的方法为:
ve[0] = 0
ve[k] = max(ve[j] + len<Vj, Vk>)
事件的最迟发生时间:vl[k]
vl[k]是指在不推迟整个工期的前提下,事件Vk允许的最迟发生时间。根据AOE网的性质,只有顶点Vk代表的事件发生,从Vk出发的活动<Vk, Vj>才能开始,而活动<Vk, Vj>的最晚开始时间为 vl[k] = vl[j] - len<Vk, Vj>。
活动的最早发生时间:ee[i]
ai由有向边<Vk, Vj>,根据AOE网的性质,只有顶点Vk代表的事件发生,活动ai才能开始,即活动ai的最早开始时间等于事件Vk的最早开始时间。
活动的最迟发生时间:el[i]
el[i]是指在不推迟真个工期的前提下,活动ai必须开始的最晚时间。若活动ai由有向边<Vk, Vj>表示,则ai的最晚开始时间要保证事件vj的最迟发生时间不拖后。
案例:
原始AOE网:

事件的最早发生时间:ve[k]
从源点向终点方向计算
ve[0] = 0
ve[1] = ve[0] + a0 = 0 + 4 = 4
ve[2] = max( ve[0] + a1, ve[1] + a2 ) = max(0 + 3, 4 + 2 = 6
ve[3] = max(ve[1] + a4, ve[2] + a3) = max(4 + 6, 3 + 4) = 10
事件的最迟发生时间:vl[k]
从终点向源点方向计算
vl[3] = ve[3] = 10
vl[2] = vl[3] - a3 = 10 - 4 = 6
vl[1] = min(vl[3] - a4, vl[2] - a2) = min(10-6, 6-2) = 4
vl[0] = min(vl[2] - a1, vl[1] - a0) = min(4-4, 4-2) = 0
活动的最早发生时间:ee[i]
共有五个活动:
ee[0] = ve[0] = 0
ee[1] = ve[0] = 0
ee[2] = ve[1] = 4
ee[3] = ve[2] = 6
ee[4] = ve[1] = 4
活动的最迟发生时间:el[i]
el[0] = v[1] - a0 = 4 - 4 = 0
el[1] = vl[2] - a1 = 6 - 3 = 3
el[2] = vl[2] - a2 = 6 - 2 = 4
el[3] = vl[3] - a3 = 10 - 4 = 6
el[4] = vl[3] - a4 = 10 - 6 = 4
活动的最早开始时间和最晚开始时间相等,则说明该活动时属于关键路径上的活动,即关键活动。
经过比较,得出关键活动有:a0, a2, a3, a4,画出示意图如下:
该AOE网有两条关键路径。
所以,通过此案例也可以发现,一个AOE网的关键路径可能有多条。






















 2461
2461











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








