Mamba和S4解读

序列建模

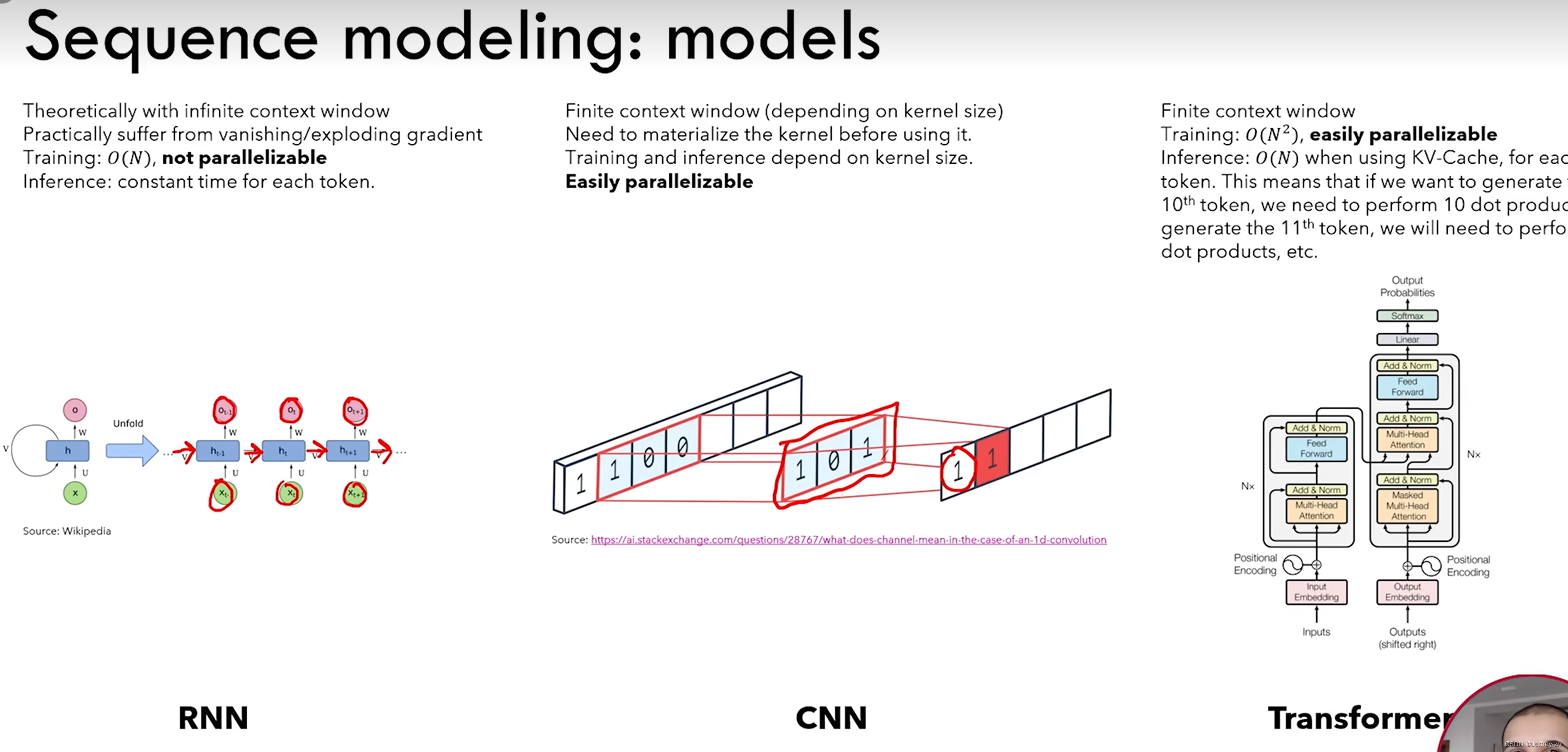
时间复杂度与并行化

RNN：O(N),不可并行
CNN：可以并行
Transformer：O($N^2$)，可以并行（训练时）；不利于扩展到长序列

理想的模型

可以并行化训练，又能够像RNN一样有线性的时间复杂度，同时可以预测每一个token的时候只需要恒定的内存消耗（例如像RNN一样O(1)）

Transforme预测第i个token时需要计算前i个token的注意力机制，是O（$N^2$)

State space models

这个状态表示是线性的，与时间无关；
首先因为计算机总是处理离散信号，因此需要将这个系统离散化，并求h(t)的近似解

离散化状态函数h(t)推导

将导数由定义展开，最终得到一个循环方程式
举例

当利用时间步delta=1时其上升比较缓慢，与解析解函数不会完全重合

State space model状态推导

由如下公式

以及State space model的定义

可知：

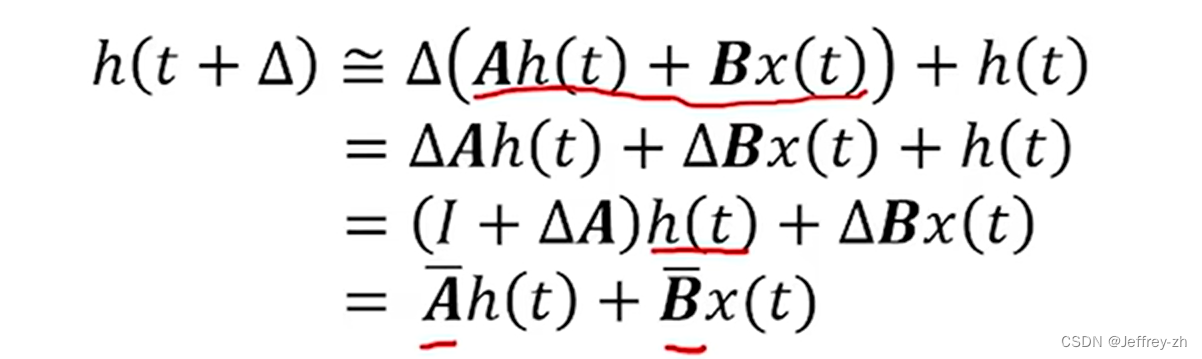
正式论文中的离散化方法

ZOH方法，与上面不同但思想一致，都是利用delta的边缘化来计算近似解。

在实际计算过程中我们不会指定步长delta，而是设置为参数，让模型自己去学习
这样我们可以得到类似RNN的计算公式

Mamba的训练

上面的结构非常适合大模型推理，每次推理时不会关注过去的状态，但不太适合训练
利用卷积计算实现并行化

上述公式的输出可以利用一个卷积核K来实现：

可以证明卷积运算的结果与推导出来的上式相同

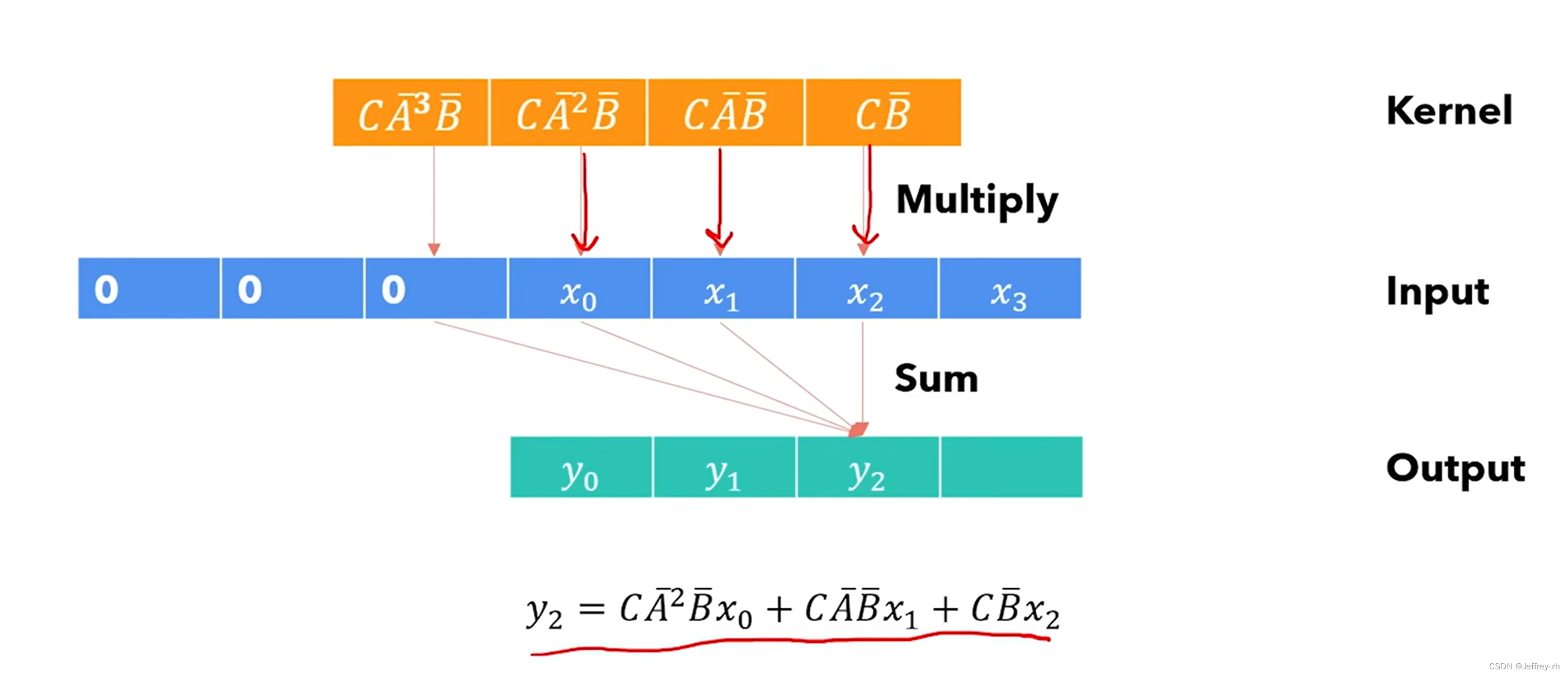
一个yk的计算可以放在GPU的一个线程上完成，虽然构建卷积核可能很昂贵但是这加快了速度

A bar矩阵捕获了之前所有的状态信息

为了达到这种效果，作者使用了HIPPO理论，去利用之前的输入信号构建当前时刻的输入信号；与傅里叶变化的差距是，对最近的信号拟合较好，对于较远的拟合平均值

对于每个维度都需要一个SSM，类似Transformer的多头

Mamba优化

SSM的一些难点

1. SSM能做到什么：
   
2. SSM不能做到：
   

Mamba和S4区别

B，C，Delta由输入的函数决定，不再固定；因此不能使用卷积来评估，这里作者用了一种SCAN的操作

并行化SCAN，由于满足结合律

最后进行了一些工程上的优化：Parellel scan、 kernel fusion、recomputation