题目正在录入中,未完待续
10

证明:

设 ( C E F ) (CEF) (CEF) 与 ( B E G ) (BEG) (BEG) 交于 E E E, H ′ H' H′.
∠ E H ′ F = π − ∠ E C F = ∠ G B E = π − ∠ G H ′ E \angle EH'F=\pi-\angle ECF=\angle GBE=\pi-\angle GH'E ∠EH′F=π−∠ECF=∠GBE=π−∠GH′E, 所以 G G G, H ′ H' H′, F F F 共线.
过 F F F 作 G E GE GE 的平行线交直线 B C BC BC 于 J J J.
显然 ∠ G B E ∼ ∠ F C J \angle GBE \sim \angle FCJ ∠GBE∼∠FCJ.
∠ G H ′ E = ∠ G E B = ∠ F J C \angle GH'E=\angle GEB=\angle FJC ∠GH′E=∠GEB=∠FJC, 所以 H ′ H' H′, F F F, J J J, B B B 共圆.
下面证明 B B B, D D D, J J J, F F F 共圆.
只需证明 ∠ C D J + ∠ C F J + ∠ B F C = π − ∠ B D C = ∠ B A C \angle CDJ+\angle CFJ+\angle BFC=\pi-\angle BDC=\angle BAC ∠CDJ+∠CFJ+∠BFC=π−∠BDC=∠BAC.
∠ C F J = ∠ B G E \angle CFJ=\angle BGE ∠CFJ=∠BGE.
∠ B F C = ∠ G B A \angle BFC=\angle GBA ∠BFC=∠GBA.
等价于 ∠ A G E = ∠ C D J \angle AGE=\angle CDJ ∠AGE=∠CDJ.
∠ D C J = ∠ D A B = ∠ E A C \angle DCJ=\angle DAB=\angle EAC ∠DCJ=∠DAB=∠EAC.
C D / C J = C D / B E ⋅ B E / C J CD/CJ=CD/BE \cdot BE/CJ CD/CJ=CD/BE⋅BE/CJ.
显然 △ B A E ∼ △ D A C \triangle BAE \sim \triangle DAC △BAE∼△DAC.
C D / B E = A C / A E CD/BE=AC/AE CD/BE=AC/AE.
B E / C J = B G / C F = A G / A C BE/CJ=BG/CF=AG/AC BE/CJ=BG/CF=AG/AC.
代入得 C D / C J = A G / A E CD/CJ=AG/AE CD/CJ=AG/AE.
△ G A E ∼ △ D C J \triangle GAE \sim \triangle DCJ △GAE∼△DCJ.
所以 ∠ A G E = ∠ C D J \angle AGE=\angle CDJ ∠AGE=∠CDJ 成立.
由此可知点 H H H 在 ( B D F ) (BDF) (BDF) 上, 进而 H ′ H' H′ 即为点 H H H.
证毕.
11

证明:

设 O B OB OB 交 A E AE AE 于 X X X, O C OC OC 交 A F AF AF 于 Y Y Y.
显然 O B OB OB 垂直平分 A E AE AE, O C OC OC 垂直平分 A F AF AF.
X X X 到 ⨀ O \bigodot O ⨀O 的幂(如无特别说明本题中所提到的圆幂均值圆幂的绝对值)为 A X 2 AX^2 AX2, 到圆 ⨀ P \bigodot P ⨀P 的幂为 O X ⋅ B X OX \cdot BX OX⋅BX. 由射影定理, A X 2 = O X ⋅ B X AX^2=OX \cdot BX AX2=OX⋅BX. 因此点 X X X 在 ⨀ O \bigodot O ⨀O 和 ⨀ P \bigodot P ⨀P 根轴(即 M N MN MN)上,
同理, Y Y Y 在 ⨀ O \bigodot O ⨀O 和 ⨀ P \bigodot P ⨀P 根轴(即 M N MN MN)上
所以 M N MN MN 为 △ A E F \triangle AEF △AEF 的中位线, 进而可知直线 M N MN MN 平分线段 A G AG AG.
证毕.
12

证明:

取 M M M 的对径点 N N N.
∠ D B N = ∠ N C E \angle DBN=\angle NCE ∠DBN=∠NCE, B D = C E BD=CE BD=CE, B N = N C BN=NC BN=NC, △ B D N ≃ △ E C N \triangle BDN \simeq \triangle ECN △BDN≃△ECN
N D = N E ND=NE ND=NE
取 D E DE DE 的中点 T T T
则 N T ⊥ D E NT \bot DE NT⊥DE
∠ N K M = π / 2 \angle NKM=\pi/2 ∠NKM=π/2
K K K, D D D, N N N, T T T 共圆
∠ T K N = ∠ E D N = ( π − ∠ D N E ) / 2 = ( π − ∠ B N C ) / 2 = ∠ N B C = ∠ N K C \angle TKN=\angle EDN=(\pi-\angle DNE)/2=(\pi-\angle BNC)/2=\angle NBC=\angle NKC ∠TKN=∠EDN=(π−∠DNE)/2=(π−∠BNC)/2=∠NBC=∠NKC
K K K, T T T, C C C 共线
证毕.
13

证明:
(一)
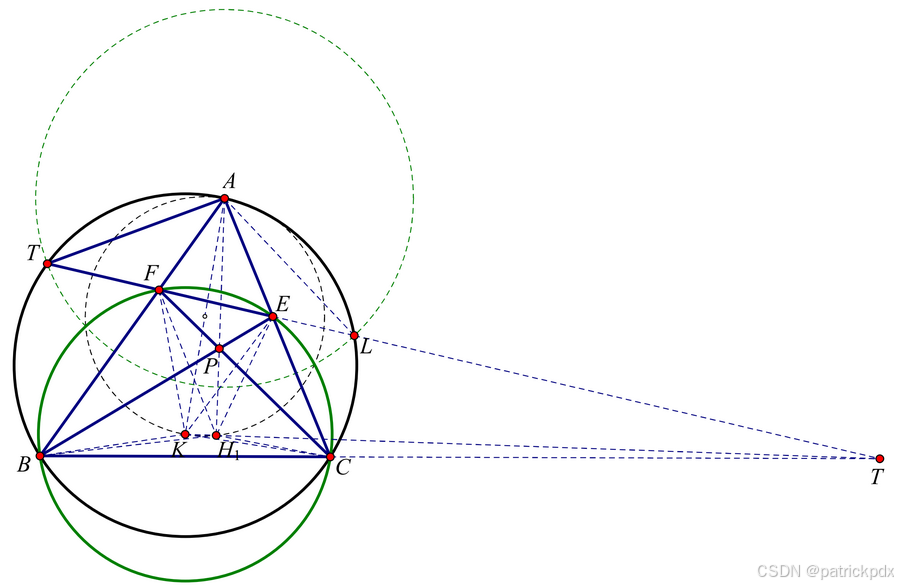
延长 F E FE FE 交 ( A B C ) (ABC) (ABC) 于点 L L L, 先证明 A T = A L AT=AL AT=AL.
设 △ A B C \triangle ABC △ABC 的外心为 O O O, 垂心为 H ′ H' H′.
△ A F E ∼ △ A C B \triangle AFE\sim \triangle ACB △AFE∼△ACB.
∠ O A B = ∠ H ′ A C \angle OAB=\angle H'AC ∠OAB=∠H′AC.
A H ′ ⊥ B C AH'\bot BC AH′⊥BC, 所以 O A ⊥ E F OA\bot EF OA⊥EF.
显然 A T = A L AT=AL AT=AL.
设完全四边形 A F P E AFPE AFPE 的密克点为 H 1 H_1 H1.
∠ F H 1 E = ∠ F H 1 A + ∠ E H 1 A = ∠ F C E + ∠ E B F = ∠ K F E \angle FH_1E=\angle FH_1A+\angle EH_1A = \angle FCE+\angle EBF=\angle KFE ∠FH1E=∠FH1A+∠EH1A=∠FCE+∠EBF=∠KFE.
所以 K K K, H 1 H_1 H1, E E E, F F F 共圆.
可类似地通过倒角证明 ∠ B K C = ∠ B H 1 C \angle BKC=\angle BH_1C ∠BKC=∠BH1C, 进而 K K K, H 1 H_1 H1, C C C, B B B 共圆.
由根心定理, K H 1 KH_1 KH1, B C BC BC, E F EF EF 共点 (记为 T T T).
由圆内接四边形的性质可知 A P AP AP 为 T T T 关于圆 K K K 的极线.
T H 1 ⋅ T K = T B ⋅ T C TH_1 \cdot TK = TB \cdot TC TH1⋅TK=TB⋅TC 等于 T T T 到圆 K K K 的幂, 结合射影定理易知 H 1 H_1 H1 在 T T T 关于圆 K K K 的极线上, 即 A A A, P P P, H 1 H_1 H1 共线.
显然 A H 1 ⊥ K H 1 AH_1 \bot KH_1 AH1⊥KH1, 进而点 H 1 H_1 H1 即为点 H H H.
显然 ( A K H ) (AKH) (AKH) 的圆心是 A K AK AK 的中点, 所以圆 A A A, 圆 K K K, ( A K H ) (AKH) (AKH) 的圆心共线, 再结合 T T T 到三圆的幂相等可知三个圆共轴于一条过 T T T 的直线 l l l.

记圆 A A A 与圆 K K K 的一个交点为点 S S S, 另一个为 S ′ S' S′, 显然 A S = A S ′ = A T AS=AS'=AT AS=AS′=AT, 且 S S ′ SS' SS′ 被 A K AK AK 垂直平分. 进而可知 △ A S P ∼ △ A H S \triangle ASP \sim \triangle AHS △ASP∼△AHS, A S 2 = A P ⋅ A H = A T 2 = A M 2 = A N 2 AS^2=AP \cdot AH=AT^2=AM^2=AN^2 AS2=AP⋅AH=AT2=AM2=AN2.
进而可知 △ A P M ∼ △ A M H \triangle APM \sim \triangle AMH △APM∼△AMH, P M / M H = A P / A M PM/MH=AP/AM PM/MH=AP/AM, 同理, P N / N H = A P / A N PN/NH=AP/AN PN/NH=AP/AN, A M = A N AM=AN AM=AN, 进而易得出本题结论.
证毕.
(二)
延长 F E FE FE 交 ( A B C ) (ABC) (ABC) 于点 L L L, 同 (一) 证明 A T = A L AT=AL AT=AL. H H H 是完全四边形 A F P E AFPE AFPE 的密克点.
证明 △ A M P ∼ △ A H M \triangle AMP\sim\triangle AHM △AMP∼△AHM, △ A N P ∼ △ A H P \triangle ANP\sim\triangle AHP △ANP∼△AHP :
由引理, A T = A L AT=AL AT=AL.
△ A T F ∼ △ A B T \triangle ATF \sim \triangle ABT △ATF∼△ABT, 所以 A F ⋅ A B = A T 2 = A M 2 = A N 2 AF\cdot AB=AT^2=AM^2=AN^2 AF⋅AB=AT2=AM2=AN2.
由 P P P, H H H, B B B, F F F 共圆可知 A F ⋅ A B = A P ⋅ A H AF \cdot AB = AP \cdot AH AF⋅AB=AP⋅AH.
A P ⋅ A H = A M 2 AP\cdot AH=AM^2 AP⋅AH=AM2, △ A M P ∼ △ A H M \triangle AMP \sim \triangle AHM △AMP∼△AHM, 同理 △ A N P ∼ △ A H P \triangle ANP \sim \triangle AHP △ANP∼△AHP.
进而易得出本题结论.
14

证明:

∠ P A E = ∠ P F E = ∠ A B C \angle PAE=\angle PFE=\angle ABC ∠PAE=∠PFE=∠ABC, ∠ A P F = ∠ P E F = ∠ A C B \angle APF=\angle PEF=\angle ACB ∠APF=∠PEF=∠ACB
所以 △ P E F ∼ △ P B C \triangle PEF \sim \triangle PBC △PEF∼△PBC
∠ B A D = ∠ D P F \angle BAD = \angle DPF ∠BAD=∠DPF, ∠ C A D = ∠ E P D \angle CAD=\angle EPD ∠CAD=∠EPD
所以 F K / E K = B D / C D FK/EK=BD/CD FK/EK=BD/CD.
15

证明:

作 ( C E B ) (CEB) (CEB), 交 ( A D E ) (ADE) (ADE) 于 E E E, G G G.
由根心定理, G E GE GE, A F AF AF, B C BC BC 三线共点, 进而 G G G, E E E, P P P 共线.
∠ G A C = ∠ G D B \angle GAC=\angle GDB ∠GAC=∠GDB.
∠ G B D = ∠ G C A \angle GBD=\angle GCA ∠GBD=∠GCA.
结合 B D = A C BD=AC BD=AC.
△ G A C ≃ △ G D B \triangle GAC \simeq \triangle GDB △GAC≃△GDB.
G A = G D GA=GD GA=GD, G B = G C GB=GC GB=GC.
∠ B G C = ∠ A G D \angle BGC=\angle AGD ∠BGC=∠AGD.
△ G A D ∼ △ G B C \triangle GAD \sim \triangle GBC △GAD∼△GBC.
∠ P E C = ∠ G B C = ∠ G A D = ∠ D E F \angle PEC=\angle GBC=\angle GAD=\angle DEF ∠PEC=∠GBC=∠GAD=∠DEF.
证毕.
16

证明:

设 ∠ C F E = a \angle CFE=a ∠CFE=a, 则 ∠ G B A = π / 2 − a \angle GBA=\pi/2-a ∠GBA=π/2−a, ∠ F D A = π / 2 + a \angle FDA=\pi/2+a ∠FDA=π/2+a, 所以 B B B, K K K, D D D, A A A 共圆.
∠ K L A = ∠ K B A = π / 2 − a \angle KLA=\angle KBA=\pi/2-a ∠KLA=∠KBA=π/2−a, ∠ K A L = ∠ K D A − π / 2 = a \angle KAL=\angle KDA-\pi/2=a ∠KAL=∠KDA−π/2=a, 只需证明 ∠ P K L = a \angle PKL=a ∠PKL=a.
若可证明 K K K, F F F, P P P, A A A 四点共圆, 则 ∠ K P A = ∠ K F A = π / 2 − 2 a \angle KPA=\angle KFA=\pi/2-2a ∠KPA=∠KFA=π/2−2a, ∠ P K L = ∠ K L A − ∠ K P A = a \angle PKL=\angle KLA-\angle KPA=a ∠PKL=∠KLA−∠KPA=a.
证明 K K K, F F F, P P P, A A A 四点共圆: ∠ P F K = π − a \angle PFK=\pi-a ∠PFK=π−a, 所以 ∠ P F K + ∠ K A L = π \angle PFK+\angle KAL=\pi ∠PFK+∠KAL=π. K K K, F F F, P P P, A A A 四点共圆.
证毕.
17

证明:

作
A
A
A,
D
D
D,
B
B
B,
C
C
C 关于
P
P
P 的对称点
A
′
A'
A′,
D
′
D'
D′,
B
′
B'
B′,
C
′
C'
C′.
显然, A ′ A' A′, D ′ D' D′, B ′ B' B′, C ′ C' C′ 共于一个和 ⨀ O \bigodot O ⨀O 相等的圆上; O ′ O' O′, P P P, O O O 共线, 且 O P = O ′ P OP=O'P OP=O′P.
显然 A ′ A' A′, D ′ D' D′, B B B, C C C 共圆.
设 A ′ D ′ A'D' A′D′ 与 B C BC BC 交于 F ′ F' F′.
F ′ A ′ ⋅ F ′ D ′ = F ′ B ⋅ F ′ C F'A'\cdot F'D'=F'B \cdot F'C F′A′⋅F′D′=F′B⋅F′C, F ′ F' F′ 在 ⨀ O \bigodot O ⨀O 和 ⨀ O ′ \bigodot O' ⨀O′ 的根轴上.
F ′ O = F ′ O ′ F'O=F'O' F′O=F′O′, 结合 O P = O ′ P OP=O'P OP=O′P 可知 F ′ O F'O F′O 垂直于 O O ′ OO' OO′, 进而可知 F ′ F' F′ 即为 F F F.
P E / / A ′ F / / A D PE//A'F//AD PE//A′F//AD.
证毕.
18

证明:

∠ A P D = ∠ F M A \angle APD=\angle FMA ∠APD=∠FMA, ∠ A P E = π − ∠ A N F = ∠ F M A \angle APE=\pi-\angle ANF=\angle FMA ∠APE=π−∠ANF=∠FMA
P P P, D D D, E E E 共线.
( A D M ) (ADM) (ADM) 的半径与 ( A E N ) (AEN) (AEN) 的半径之比为 A D / sin ∠ A P D A E / sin ∠ A P E = 1 \frac{AD/\sin \angle APD}{AE / \sin \angle APE}=1 AE/sin∠APEAD/sin∠APD=1.
所以 ∠ P M A = ∠ P N A \angle PMA=\angle PNA ∠PMA=∠PNA.
∠ M P A = ∠ M D A = ∠ B D F \angle MPA=\angle MDA=\angle BDF ∠MPA=∠MDA=∠BDF.
∠ A P N = ∠ A E N = ∠ C E F \angle APN=\angle AEN=\angle CEF ∠APN=∠AEN=∠CEF.
由 A D AD AD, A E AE AE 与 ⨀ K \bigodot K ⨀K 相切可知 ∠ M P A + ∠ A P N = π − ∠ D F E = ∠ M A N \angle MPA+\angle APN=\pi-\angle DFE=\angle MAN ∠MPA+∠APN=π−∠DFE=∠MAN.
进而易知 A M P N AMPN AMPN 为平行四边形.
证毕.
19

证明:

∠ P O A = 2 B − x \angle POA=2B-x ∠POA=2B−x
∠ O F P = ∠ O A P = p i / 2 − 2 B + x \angle OFP=\angle OAP=pi/2-2B+x ∠OFP=∠OAP=pi/2−2B+x
∠ O F E = ∠ O A C = π / 2 − B \angle OFE=\angle OAC=\pi/2-B ∠OFE=∠OAC=π/2−B
∠ P F E = ∠ O F E − ∠ O F P = B − x = ∠ K B A \angle PFE=\angle OFE-\angle OFP=B-x=\angle KBA ∠PFE=∠OFE−∠OFP=B−x=∠KBA
20

证明:

∠ A F G = ∠ D A B + ∠ A D E \angle AFG=\angle DAB+\angle ADE ∠AFG=∠DAB+∠ADE.
∠ A P D = ∠ A D P = ∠ D A B + ∠ D B A \angle APD=\angle ADP=\angle DAB+\angle DBA ∠APD=∠ADP=∠DAB+∠DBA.
A D = A E AD=AE AD=AE, 所以 ∠ D B A = ∠ A D E \angle DBA=\angle ADE ∠DBA=∠ADE.
进而 ∠ A F G = ∠ A P D \angle AFG=\angle APD ∠AFG=∠APD, P P P, A A A, F F F, D D D 四点共圆.
可以类似地证明: K K K, A A A, G G G, E E E 四点共圆. (过程略)
∠ F P A = ∠ A D E = ∠ A E D = ∠ G K A \angle FPA=\angle ADE=\angle AED=\angle GKA ∠FPA=∠ADE=∠AED=∠GKA.
A P = A K ⇒ ∠ A P K = ∠ A K P AP=AK \Rightarrow \angle APK=\angle AKP AP=AK⇒∠APK=∠AKP.
进而 ∠ F P K = ∠ G K P \angle FPK=\angle GKP ∠FPK=∠GKP, P H = P K PH=PK PH=PK.
结合 A P = A K AP=AK AP=AK 可知 A H AH AH 垂直平分 P K PK PK.
证毕.
21

证明:

∠
I
P
B
=
∠
I
Q
B
=
∠
I
B
Q
\angle IPB = \angle IQB=\angle IBQ
∠IPB=∠IQB=∠IBQ, 进而有
△
I
B
R
∼
△
I
P
B
\triangle IBR \sim \triangle IPB
△IBR∼△IPB.
I B 2 = I P ⋅ I R = I D 2 IB^2=IP \cdot IR=ID^2 IB2=IP⋅IR=ID2.
进而有 △ I D P ∼ △ I R D \triangle IDP \sim \triangle IRD △IDP∼△IRD.
∠ R B E + ∠ I D R = ∠ B R D \angle RBE+\angle IDR=\angle BRD ∠RBE+∠IDR=∠BRD.
∠ I D E = π 2 − ∠ I D B = π − ∠ B R D \angle IDE=\frac{\pi}{2}-\angle IDB=\pi-\angle BRD ∠IDE=2π−∠IDB=π−∠BRD.
所以 ∠ R B E + ∠ I D R + ∠ I D E = π \angle RBE+\angle IDR+\angle IDE=\pi ∠RBE+∠IDR+∠IDE=π, E E E, B B B, R R R, D D D 四点共圆.
∠ B R E = ∠ B D E = π 2 \angle BRE=\angle BDE=\frac{\pi}{2} ∠BRE=∠BDE=2π.
证毕.
22

证明:

∠ K B Q = ∠ K Q B = ∠ K P B \angle KBQ=\angle KQB=\angle KPB ∠KBQ=∠KQB=∠KPB, 由此可知 △ K B P ∼ △ K R B \triangle KBP \sim \triangle KRB △KBP∼△KRB.
∴ K C 2 = K B 2 = K R ⋅ K P \therefore KC^2=KB^2=KR\cdot KP ∴KC2=KB2=KR⋅KP.
∴ △ K C R ∼ △ K R C \therefore \triangle KCR \sim \triangle KRC ∴△KCR∼△KRC.
A K ⊥ B C AK \bot BC AK⊥BC, 所以 E C ⊥ B C EC \bot BC EC⊥BC.
∠ B R C = ∠ B R K + ∠ C R K = ∠ P B K + ∠ P C K = ∠ P B A + ∠ P C B − 2 ∠ K A B = π − ∠ B A C / 2 − 2 ∠ K B A \angle BRC=\angle BRK+\angle CRK=\angle PBK+\angle PCK=\angle PBA+\angle PCB-2\angle KAB=\pi-\angle BAC/2-2\angle KBA ∠BRC=∠BRK+∠CRK=∠PBK+∠PCK=∠PBA+∠PCB−2∠KAB=π−∠BAC/2−2∠KBA.

设 ( E B C ) (EBC) (EBC) 的圆心为 O O O, 易知 O O O 在 A K AK AK 上.
取 ( E B C ) (EBC) (EBC) 和 ⨀ A \bigodot A ⨀A 的内位似中心 K ′ K' K′.
则 D A / O E = A K ′ / O K ′ DA/OE=AK'/OK' DA/OE=AK′/OK′, 所以 △ D A K ′ ∼ △ E O K ′ \triangle DAK'\sim \triangle EOK' △DAK′∼△EOK′, ∠ D K ′ A = ∠ O K ′ E \angle DK'A=\angle OK'E ∠DK′A=∠OK′E, 进而可知 D D D, K ′ K' K′, E E E 共线, K ′ K' K′ 即为 K K K.

B A / B O = A K ′ / O K ′ BA/BO=AK'/OK' BA/BO=AK′/OK′, 所以 ∠ K ′ B A = ∠ K ′ B O \angle K'BA=\angle K'BO ∠K′BA=∠K′BO.
∠ B E C = ∠ A O E = ∠ B A C / 2 + 2 ∠ K B A \angle BEC=\angle AOE=\angle BAC/2+2\angle KBA ∠BEC=∠AOE=∠BAC/2+2∠KBA.
∴ ∠ B E C + ∠ B R C = π \therefore \angle BEC+\angle BRC=\pi ∴∠BEC+∠BRC=π, 进而 E E E, C C C, R R R, B B B 共圆.
∴ ∠ E R B = ∠ E R C = π 2 \therefore \angle ERB=\angle ERC=\frac{\pi}{2} ∴∠ERB=∠ERC=2π.
证毕.
23

证明:

设 ( A E F ) (AEF) (AEF) 交 ( A B C ) (ABC) (ABC) 除 A A A 外的另一个交点为 T T T.
△ T E B ∼ △ T F C \triangle TEB \sim \triangle TFC △TEB∼△TFC. (证明略)
T C / T B = C F / B E TC/TB=CF/BE TC/TB=CF/BE.
设 ( A F B ) (AFB) (AFB) 交线段 B D BD BD 于 X X X, ( A E C ) (AEC) (AEC) 交线段 B C BC BC 于 Y Y Y.
D X = D P ⋅ D A / D B = D P ⋅ D A / D C = D Y DX=DP \cdot DA/DB=DP \cdot DA/DC=DY DX=DP⋅DA/DB=DP⋅DA/DC=DY.
B E ⋅ B A = B Y ⋅ B C = C X ⋅ B C = C F ⋅ C A ⇒ B E / C F = C A / B A BE \cdot BA=BY\cdot BC=CX \cdot BC=CF \cdot CA \Rightarrow BE/CF=CA/BA BE⋅BA=BY⋅BC=CX⋅BC=CF⋅CA⇒BE/CF=CA/BA.
T C / T B = B A / C A TC/TB=BA/CA TC/TB=BA/CA, 所以四边形 T A B C TABC TABC 构成等腰梯形 ⇒ O \Rightarrow O ⇒O 在 T A TA TA 的中垂线上 ⇒ O \Rightarrow O ⇒O 在 B C BC BC 的中垂线上.
证毕.
24

证明:

记内切圆 I I I 在 A B AB AB, A C AC AC 上的切点分别为 J J J, L L L. 设若能证明 ∠ A L T = ∠ C L S \angle ALT=\angle CLS ∠ALT=∠CLS, 则 ∠ A L T = ∠ C L S = ∠ L T S \angle ALT=\angle CLS=\angle LTS ∠ALT=∠CLS=∠LTS, T S / / A C TS//AC TS//AC. 下面证明 ∠ A L T = ∠ C L S \angle ALT=\angle CLS ∠ALT=∠CLS.
∠ A L T = ∠ C L S ⟺ ∠ L S T = ∠ L T S ⟺ L T = L S ⟺ ∠ T I L = ∠ S I L \angle ALT=\angle CLS \iff \angle LST=\angle LTS \iff LT=LS \iff \angle TIL=\angle SIL ∠ALT=∠CLS⟺∠LST=∠LTS⟺LT=LS⟺∠TIL=∠SIL.
∠ T I L = ∠ J I L − 2 ∠ F I J = ( π − A ) − 2 ( π / 2 − A − C / 2 ) = A + C \angle TIL=\angle JIL - 2\angle FIJ=(\pi-A)-2(\pi/2-A-C/2)=A+C ∠TIL=∠JIL−2∠FIJ=(π−A)−2(π/2−A−C/2)=A+C.
∠ S I L = 2 ∠ L P S \angle SIL=2\angle LPS ∠SIL=2∠LPS.
∠ L P S = π / 2 − C / 2 − ∠ S P C = π / 2 − C / 2 − ∠ S K P \angle LPS=\pi/2-C/2-\angle SPC=\pi/2-C/2-\angle SKP ∠LPS=π/2−C/2−∠SPC=π/2−C/2−∠SKP.
因为 A I / / K S AI//KS AI//KS, 所以 ∠ S K P = ∠ A I K = π − ∠ B I P − ∠ A I B = π / 2 + B / 2 − ( π / 2 + C / 2 ) = B / 2 − C / 2 \angle SKP=\angle AIK=\pi- \angle BIP -\angle AIB=\pi/2 + B/2-(\pi/2+C/2)=B/2-C/2 ∠SKP=∠AIK=π−∠BIP−∠AIB=π/2+B/2−(π/2+C/2)=B/2−C/2.
所以 ∠ L P S = π / 2 − B / 2 \angle LPS=\pi/2-B/2 ∠LPS=π/2−B/2, 进而 ∠ S I L = π − B = A + C = ∠ T I L \angle SIL=\pi-B=A+C=\angle TIL ∠SIL=π−B=A+C=∠TIL.
证毕.
25

证明:

设
D
N
DN
DN 交
B
C
BC
BC 于点
G
G
G, 设
D
M
DM
DM 交
(
A
B
C
)
(ABC)
(ABC) 于点
H
H
H.
显然 D H DH DH 为直径.
∠ H N G = ∠ G M H = π 2 \angle HNG= \angle GMH = \frac{\pi}{2} ∠HNG=∠GMH=2π, 所以 N N N, H H H, M M M, G G G 四点共圆.
倒角易知 ∠ G F C = ∠ G H C \angle GFC=\angle GHC ∠GFC=∠GHC (过程略). 进而有 G G G, F F F, H H H, C C C 四点共圆.
∠ A E F = ∠ B N D − ∠ A B N \angle AEF=\angle BND-\angle ABN ∠AEF=∠BND−∠ABN.
∠ N G B = ∠ N H M = ∠ F H C \angle NGB=\angle NHM=\angle FHC ∠NGB=∠NHM=∠FHC, 所以 ∠ N H F = ∠ D H C \angle NHF=\angle DHC ∠NHF=∠DHC.
∠ A H F = ∠ N H F − ∠ N H A = ∠ D H C − ∠ A B N = ∠ B N D − ∠ A B N = ∠ A E F \angle AHF=\angle NHF-\angle NHA=\angle DHC-\angle ABN=\angle BND-\angle ABN=\angle AEF ∠AHF=∠NHF−∠NHA=∠DHC−∠ABN=∠BND−∠ABN=∠AEF.
∴ A \therefore A ∴A, E E E, H H H, F F F 共圆.
∠ E H F = ∠ B A C = 2 ∠ D H C = 2 ∠ N H F \angle EHF=\angle BAC =2\angle DHC=2\angle NHF ∠EHF=∠BAC=2∠DHC=2∠NHF.
∴ ∠ N H F = ∠ N H E \therefore \angle NHF=\angle NHE ∴∠NHF=∠NHE.
∠ H A C = π 2 − ∠ D A C = 1 2 ( π − ∠ B A C ) \angle HAC=\frac{\pi}{2}-\angle DAC=\frac{1}{2}(\pi-\angle BAC) ∠HAC=2π−∠DAC=21(π−∠BAC).
∴ ∠ E A H = ∠ H A C \therefore \angle EAH=\angle HAC ∴∠EAH=∠HAC, E H = F H EH=FH EH=FH.
进而可知 △ E H N ≃ △ F H N \triangle EHN \simeq \triangle FHN △EHN≃△FHN, E N = F N EN=FN EN=FN.
证毕.
26

证明:

延长 B C BC BC 交 ( A B D ) (ABD) (ABD) 于 H H H.
∠ E A B = ∠ B C E = ∠ B H F ⇒ H F / / C E \angle EAB=\angle BCE=\angle BHF \Rightarrow HF//CE ∠EAB=∠BCE=∠BHF⇒HF//CE. 结合 F G / / C E FG//CE FG//CE 可知 F F F, G G G, H H H 共线.
设过 G G G 的 B C BC BC 的平行线交 B K BK BK 于点 S S S.
C G / K G = E F / K F = B S / K S ⇒ B E / / F S CG/KG=EF/KF=BS/KS \Rightarrow BE//FS CG/KG=EF/KF=BS/KS⇒BE//FS
进而 ∠ G S F = ∠ C B E = ∠ D A F = ∠ D B F \angle GSF= \angle CBE=\angle DAF= \angle DBF ∠GSF=∠CBE=∠DAF=∠DBF, B B B, G G G, F F F, S S S 四点共圆.
∠ F B S = ∠ S G F = ∠ B H F \angle FBS=\angle SGF=\angle BHF ∠FBS=∠SGF=∠BHF, 所以 B S BS BS 是 ⨀ O \bigodot O ⨀O 在 B B B 点处的切线.
证毕.
27

证明:

K P = N P ⇒ ∠ K D P = ∠ N D P KP=NP \Rightarrow \angle KDP=\angle NDP KP=NP⇒∠KDP=∠NDP.
∠ K N D = ∠ K P D = 2 ∠ K N M ⇒ ∠ K N M = ∠ D N M \angle KND=\angle KPD=2\angle KNM \Rightarrow \angle KNM=\angle DNM ∠KND=∠KPD=2∠KNM⇒∠KNM=∠DNM.
∴ M \therefore M ∴M 为 △ D N K \triangle DNK △DNK 的内心.
∠ D K M = ∠ N K M = ∠ N A M \angle DKM=\angle NKM=\angle NAM ∠DKM=∠NKM=∠NAM.
∴ K M \therefore KM ∴KM 与 A N AN AN 的交点在 ( A B C ) (ABC) (ABC) 上.
∠ O A D = ∠ K A D − π 2 = ∠ D K M \angle OAD=\angle KAD-\frac{\pi}{2}=\angle DKM ∠OAD=∠KAD−2π=∠DKM.
∴ A \therefore A ∴A, N N N, O O O 共线, 即 O O O 在 ( K M D ) (KMD) (KMD) 上.
28


证明:

∠ K B Q = ∠ K Q B = ∠ K P B \angle KBQ=\angle KQB=\angle KPB ∠KBQ=∠KQB=∠KPB, 由此可知 △ K B P ∼ △ K R B \triangle KBP \sim \triangle KRB △KBP∼△KRB.
∴ K C 2 = K B 2 = K R ⋅ K P \therefore KC^2=KB^2=KR\cdot KP ∴KC2=KB2=KR⋅KP.
∴ △ K C R ∼ △ K R C \therefore \triangle KCR \sim \triangle KRC ∴△KCR∼△KRC.
A K ⊥ B C AK \bot BC AK⊥BC, 所以 E C ⊥ B C EC \bot BC EC⊥BC.
∠ B R C = ∠ B R K + ∠ C R K = ∠ P B K + ∠ P C K = ∠ P B A + ∠ P C B − 2 ∠ K A B = π − ∠ B A C / 2 − 2 ∠ K B A \angle BRC=\angle BRK+\angle CRK=\angle PBK+\angle PCK=\angle PBA+\angle PCB-2\angle KAB=\pi-\angle BAC/2-2\angle KBA ∠BRC=∠BRK+∠CRK=∠PBK+∠PCK=∠PBA+∠PCB−2∠KAB=π−∠BAC/2−2∠KBA.
设 ( E B C ) (EBC) (EBC) 的圆心为 O O O, 易知 O O O 在 A K AK AK 上.
取 ( E B C ) (EBC) (EBC) 和 ⨀ A \bigodot A ⨀A 的内位似中心 K ′ K' K′.
则 D A / O E = A K ′ / O K ′ DA/OE=AK'/OK' DA/OE=AK′/OK′, 所以 △ D A K ′ ∼ △ E O K ′ \triangle DAK'\sim \triangle EOK' △DAK′∼△EOK′, ∠ D K ′ A = ∠ O K ′ E \angle DK'A=\angle OK'E ∠DK′A=∠OK′E, 进而可知 D D D, K ′ K' K′, E E E 共线, K ′ K' K′ 即为 K K K.
B A / B O = A K ′ / O K ′ BA/BO=AK'/OK' BA/BO=AK′/OK′, 所以 ∠ K ′ B A = ∠ K ′ B O \angle K'BA=\angle K'BO ∠K′BA=∠K′BO.
∠ B E C = ∠ A O E = ∠ B A C / 2 + 2 ∠ K B A \angle BEC=\angle AOE=\angle BAC/2+2\angle KBA ∠BEC=∠AOE=∠BAC/2+2∠KBA.
∴ ∠ B E C + ∠ B R C = π \therefore \angle BEC+\angle BRC=\pi ∴∠BEC+∠BRC=π, 进而 E E E, C C C, R R R, B B B 共圆.
∴ ∠ E R B = ∠ E R C = π 2 \therefore \angle ERB=\angle ERC=\frac{\pi}{2} ∴∠ERB=∠ERC=2π.
证毕.
29 已知 △ A B C \triangle ABC △ABC, ∠ B A C \angle BAC ∠BAC 的平分线交 △ A B C \triangle ABC △ABC 的外接圆于点 D D D, 作 E F / / B C EF//BC EF//BC 交 D B DB DB, D C DC DC 分别于点 E E E, F F F, ( B D F ) (BDF) (BDF) 交 A B AB AB 于点 B B B, M M M, ( C D E ) (CDE) (CDE) 交 A C AC AC 于点 C C C, N N N. 求证: A M = A N AM=AN AM=AN.

证明:
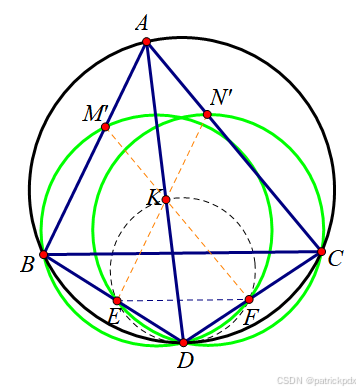
设 ( D E F ) (DEF) (DEF) 交 A D AD AD 于点 K K K, 则 ∠ E K D = ∠ D F E = ∠ D C B = A / 2 \angle EKD=\angle DFE=\angle DCB=A/2 ∠EKD=∠DFE=∠DCB=A/2, ∠ F K D = ∠ D E F = ∠ D B C = A / 2 \angle FKD=\angle DEF=\angle DBC=A/2 ∠FKD=∠DEF=∠DBC=A/2. 进而 ∠ E K D = ∠ B A D \angle EKD=\angle BAD ∠EKD=∠BAD, E K / / A B EK//AB EK//AB, ∠ D K F = ∠ D A C \angle DKF =\angle DAC ∠DKF=∠DAC, F K / / A C FK//AC FK//AC.
延长 E K EK EK, F K FK FK, 分别交 A B AB AB, A C AC AC 于 M ′ M' M′, N ′ N' N′.
易知 ∠ A B D + ∠ M ′ F D = ∠ A B D + ∠ A C D = π \angle ABD+\angle M'FD=\angle ABD+\angle ACD=\pi ∠ABD+∠M′FD=∠ABD+∠ACD=π, M ′ M' M′ 在 ( B D F ) (BDF) (BDF) 上, M ′ M' M′ 即为 M M M.
类似地, 可证明 N ′ N' N′ 即为 N N N.
显然四边形 A M K N AMKN AMKN 是菱形, 因此 A M = A N AM=AN AM=AN.
证毕.
整理时间: 2025年2月22日
























 858
858

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








