【离散】画哈斯图--最好理解绝不会出错

离散数学哈斯图的画法

两个步骤：
第一步：排点的层数
第二步：把有关系的点连接起来

看一道题：

设A={1,2,3,4,6,8,9}，偏序集S={A,《 },其中《为整除关系，请画出S的哈斯图

首先把他们的所有的关系列出来（后面的数可以整除前面的数，这两个数就有整除的关系）

<1,2> <1,3> <1,4> <1,6> <1,8> <1,9>

<2,4> <2,6> <2,8>

<3,6> <3,9>

<4,8>

然后来排点的层数。

首先看，所有关系里面不在值域的元素有哪几个：最先找到的是1

所以我们把1放到第一层

然后我们删掉<1,x>的所有元素(之后就不考虑那些元素)

<1,2> <1,3> <1,4> <1,6> <1,8> <1,9>

<2,4> <2,6> <2,8>

<3,6> <3,9>

<4,8>

继续找（没被加入哈斯图的）不出现在值域的元素，我们找到了2，3，那么把2，3放在第二排.
同样删除<2,x>和<3,x>的所有元素

<1,2> <1,3> <1,4> <1,6> <1,8> <1,9>

<2,4> <2,6> <2,8>

< 3,6> < 3,9>

<4,8>

这时不出现在值域且没被加入哈斯图的元素有4，6，9。那么把4，6，9放到第三排。

最后还剩下8，那么把8放在第四排。
在这里插入图片描述

现在我们点的排序就排好了。

最后把每一层之间有关系的点连起来就好了。

⚠️注意，这里每一层只会和上一层相连，不会跨两层连。

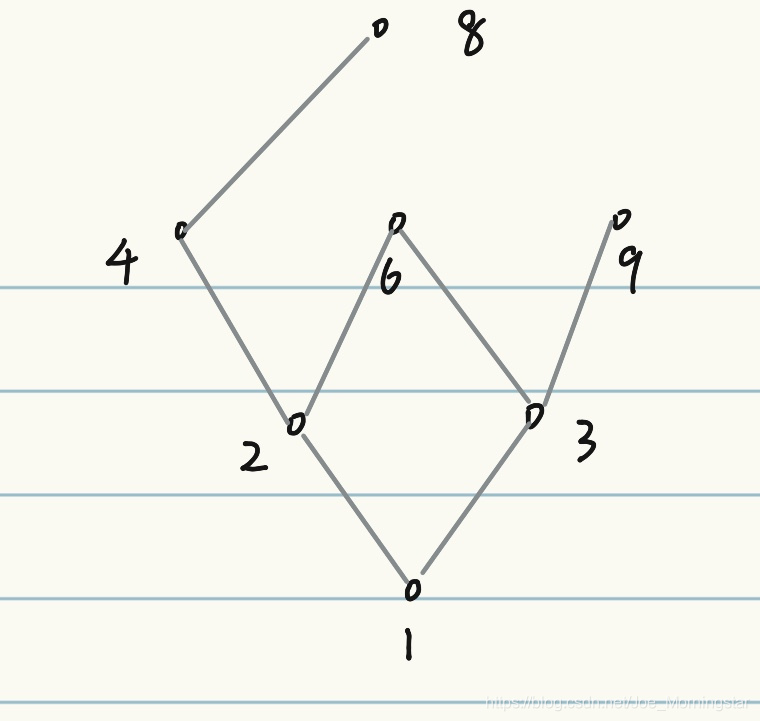
有帮助的话就给我点个赞吧！
5个赞更新极大极小元。

更新一下极大极小元：
极小元就是 没有元素比它小
如果有的关系只有它自己 那么也是极小的 那也是极小元
极大元同理 ：）

---

楼主最近在准备保研 要复习专业课内容

大家如果有什么想看的科目也可以评论我 （毕竟我都会复习到）