题目来源:力扣(LeetCode)和传说
链接:https://leetcode-cn.com/problems
特别鸣谢:来自夸夸群的 醉笑陪公看落花@知乎,王不懂不懂@知乎,QFIUNE@csdn
感谢任老师倾囊相授,感谢小伙伴们督促学习,一起进步
leetcode 11 容器
给你 n 个非负整数 a1,a2,…,an,每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线,垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0) 。找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
说明:你不能倾斜容器。

思路:双指针,先找最宽,再找最高
指针从两头往中间走,每次向内移动短柱子的指针,计算面积,最后给出最大值即可
t O(n)
def solve(self, height):
n = len(height)
max_area = 0
j = n-1
i = 0
while(i<j):
max_area = max(min(height[j],height[i])*(j-i),max_area)
if height[i]<height[j]:i +=1
else:j-=1
return max_area
leetcode 42 接雨水
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
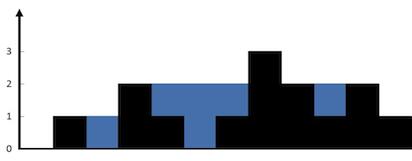
给出了三种方案,第一种是穷举,超时,其他两种测试通过
双指针:即是找最大桶
'''
穷举 超时
'''
# class Solution:
# def solve(self, height):
# sum_area = 0
# n = len(height)
# for i in range(1,n-1):
# left_edge = height[0]
# right_edge = height[n - 1]
# for j in range(n):
# if j<i:left_edge = max(left_edge,height[j])
# else:right_edge = max(right_edge,height[j])
# m_area = min(right_edge,left_edge)-height[i]
# sum_area += m_area if m_area >0 else 0
# print(i,sum_area,left_edge,right_edge)
# return sum_area
'''
找左右墙 通过
'''
# class Solution:
# def solve(self, height):
# sum_area = 0
# n = len(height)
# lw = [0]*n # lw[i] 第i根柱子的左墙高度
# rw = [0]*n # lw[i] 第i根柱子的左墙高度
# for i in range(1,n-1):
# # 找左墙
# lw[i] = max(lw[i-1],height[i-1])
# for i in range(n-2,0,-1):
# # 找右墙
# rw[i] = max(rw[i+1],height[i+1])
#
# for i in range(1,n-1):
# m_area = min(lw[i], rw[i]) - height[i]
# sum_area += m_area if m_area >0 else 0
# return sum_area
'''
双指针 通过
'''
class Solution:
def solve(self, height):
ans = 0
left = 0
right = len(height)-1
if right<=0:
return 0
lw = height[left]
rw = height[right]
while(left<right):
if lw<=rw:
left += 1
if lw<=height[left]:
lw = height[left]
else:
ans += lw-height[left]
else:
right -= 1
if rw<=height[right]:
rw = height[right]
else:
ans += rw-height[right]
return ans
leetcode 407 二维雨水
给你一个 m x n 的矩阵,其中的值均为非负整数,代表二维高度图每个单元的高度,请计算图中形状最多能接多少体积的雨水。
示例:
给出如下 3x6 的高度图:
[
[1,4,3,1,3,2],
[3,2,1,3,2,4],
[2,3,3,2,3,1]
]
返回 4 。
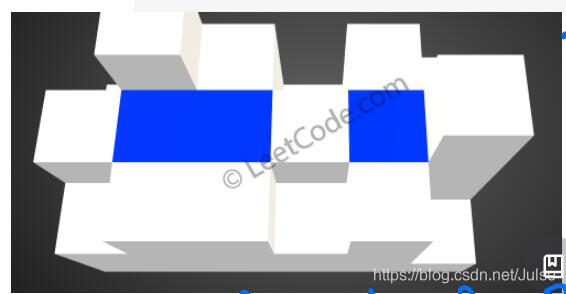
主要用到了小顶堆找最矮墙,数组记录节点是否访问过
小顶堆 查找t O(1) 插入t O(log2n)
def solve(self, height):
# 找最大的桶,装水
ans = 0
# 找墙 小于3*3 只有墙,没有容器
if len(height)<3:return 0
if len(height[0])<3:return 0
m = len(height)
n = len(height[0])
import heapq
w = []
# v = [[0]*n]*m # 会是一个相同的地址被存储n遍,每次修改其中一个的时候,其他的也会被改掉。
v = [[True for i in range(n)] for i in range(m)]
i = 0
for j in range(n):
v[i][j] = False
heapq.heappush(w,(height[i][j],i,j))
i = m-1
for j in range(n):
v[i][j] = False
heapq.heappush(w,(height[i][j],i,j))
j = 0
for i in range(1,m-1):
v[i][j] = False
heapq.heappush(w,(height[i][j],i,j))
j = n-1
for i in range(1,m-1):
v[i][j] = False
heapq.heappush(w,(height[i][j],i,j))
# 找容器
# [1:m-2,1:n-2]
while(w!=[]):
min_w = heapq.heappop(w)
# 前后左右
i = min_w[1]
j = min_w[2]
# 非墙 有些地方会被算两遍
for p,q in [[1,0],[-1,0],[0,1],[0,-1]]:
if i+p>0 and j+q>0 and i+p<m-1 and j+q<n-1 and v[i+p][j+q]:
if min_w[0] > height[i+p][j+q]:
ans += min_w[0] - height[i+p][j+q]
heapq.heappush(w, (min_w[0], i+p,j+q))
else:
heapq.heappush(w, (height[i+p][j+q], i+p,j+q))
v[i+p][j+q] = False
return ans
拓展题目:把二维雨水题改成求坑的数目
连通的坑算一个
set() 用hash存储内容,查找t O(1),插入 t O(1)
找连通坑的两种方案:
广度优先:借助队列实现,Queue
深度优先:借助递归实现
class Solution:
dig = set()
def solve(self, height):
self.height = height
# 找最大的桶,装水,能装水的是坑,坑和坑挨着算一个
# 找墙 小于3*3 只有墙,没有容器
if len(height)<3:return 0
if len(height[0])<3:return 0
m = len(height)
n = len(height[0])
import heapq
w = []
v = [[False for i in range(n)] for i in range(m)] # 图里面,一般未访问过的地方标记False
i = 0
for j in range(n):
v[i][j] = True
heapq.heappush(w,(height[i][j],i,j))
i = m-1
for j in range(n):
v[i][j] = True
heapq.heappush(w,(height[i][j],i,j))
j = 0
for i in range(1,m-1):
v[i][j] = True
heapq.heappush(w,(height[i][j],i,j))
j = n-1
for i in range(1,m-1):
v[i][j] = True
heapq.heappush(w,(height[i][j],i,j))
# 找容器
# [1:m-2,1:n-2]
while(w!=[]):
min_w = heapq.heappop(w)
# 前后左右
i = min_w[1]
j = min_w[2]
# 非墙 有些地方会被算两遍,所以要visit数组记录被访问过的地方
for p,q in [[1,0],[-1,0],[0,1],[0,-1]]:
new_i = i+p
new_j = j+q
# if i+p>0 & j+q>0 & i+p<n-1 & j+q<m-1 & v[i+p][j+q] :
# if new_i>0 and new_j>0 and new_i<m-1 and new_j<n-1 and v[new_i][new_j]:
if 0<new_i<m-1 and 0<new_j<n-1 and not v[new_i][new_j]:
if min_w[0] > height[new_i][new_j] and height[new_i][new_j] not in self.dig:# 此处有坑,坑位号记录下来
# global dig
self.dig.add((new_i,new_j))
# ans += 1
heapq.heappush(w, (min_w[0], new_i,new_j))
else:
heapq.heappush(w, (height[new_i][new_j], new_i,new_j))
v[new_i][new_j] = True
'''
算坑的数目
'''
# ans = self.BFS(m,n) # 广度优先
ans = self.DFS(m,n) # 深度优先
return ans
def BFS(self,m,n):
'''
广度优先
:return:
'''
ans = 0 # 联通坑的数目
v = [[False for i in range(n)] for i in range(m)]
from queue import Queue
for i in range(m):
for j in range(n):
if (i,j) not in self.dig or v[i][j]:continue
que = Queue(maxsize=m*n)
que.put((i, j))
v[i][j] = True
while(not que.empty()):
node = que.get()
for p,q in [[1,0],[-1,0],[0,1],[0,-1]]:
new_i = node[0]+p
new_j = node[1]+q
if 0<new_i<m-1 and 0<new_j<n-1 and not v[new_i][new_j] and (new_i,new_j) in self.dig:
que.put((new_i, new_j))
v[new_i][new_j] = True
ans+=1
return ans
def DFS(self,m,n):
'''
深度优先
:return:
'''
ans = 0 # 连通坑的数目
self.v = [[False for i in range(n)] for i in range(m)]
for i in range(m):
for j in range(n):
if (i, j) not in self.dig or self.v[i][j]:continue
self.v[i][j] = True
self.doDFS(i, j, m, n)
ans+=1
return ans
def doDFS(self,i,j,m,n):
for p, q in [[1, 0], [-1, 0], [0, 1], [0, -1]]:
new_i = i + p
new_j = j + q
if 0 < new_i < m - 1 and 0 < new_j < n - 1 and not self.v[new_i][new_j] and (new_i, new_j) in self.dig:
self.v[new_i][new_j] = True
return self.doDFS(new_i, new_j, m, n)
测试用例
# dig = 2
# height= [
# [1,4,3,1,3,2],
# [3,2,1,3,2,4],
# [2,3,3,2,3,1],
# ]
# dig = 1
height= [
[1, 4, 3, 1, 3, 2],
[3, 2, 1, 0, 2, 4],
[2, 3, 3, 2, 3, 1],
]
相关笔记
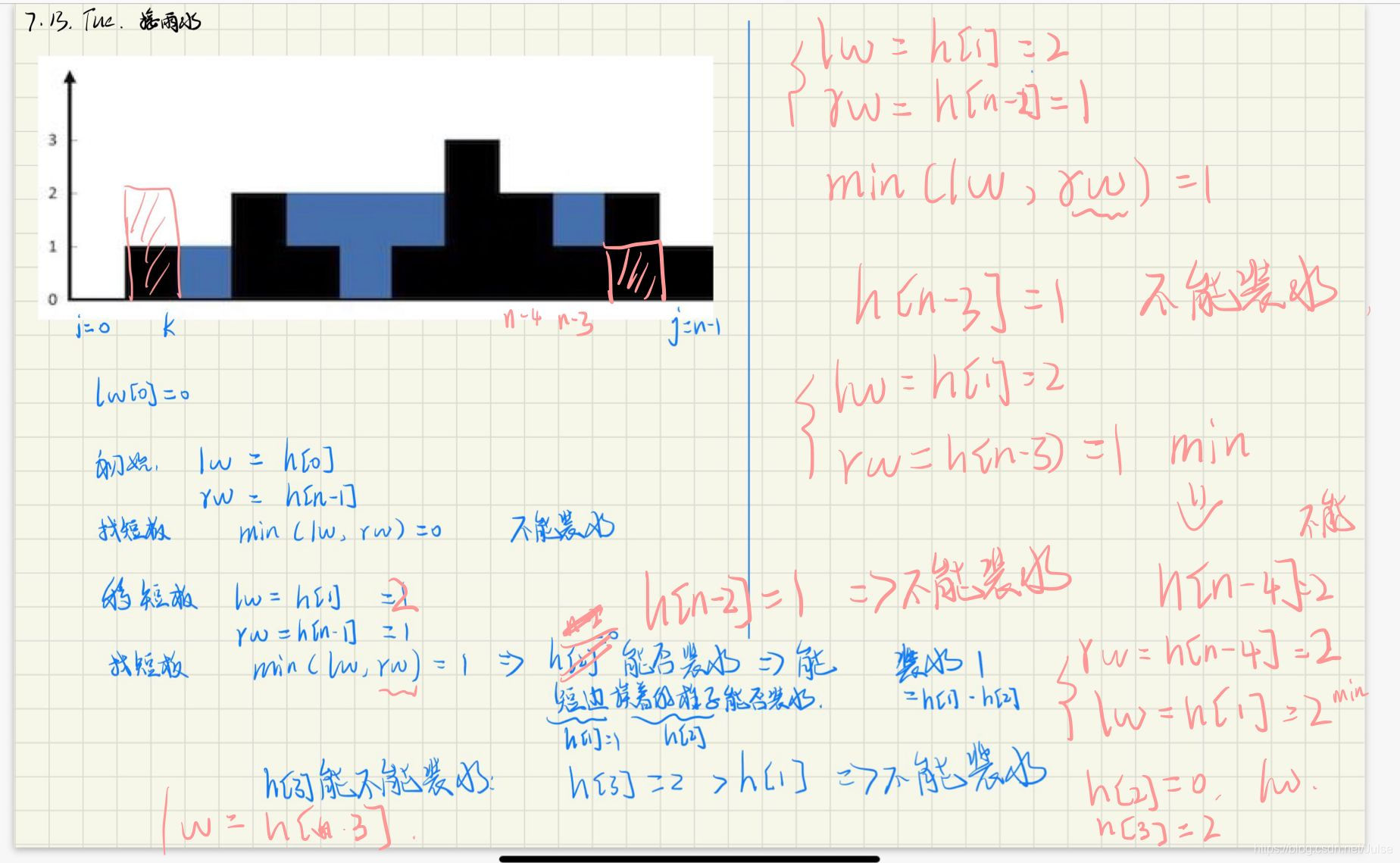
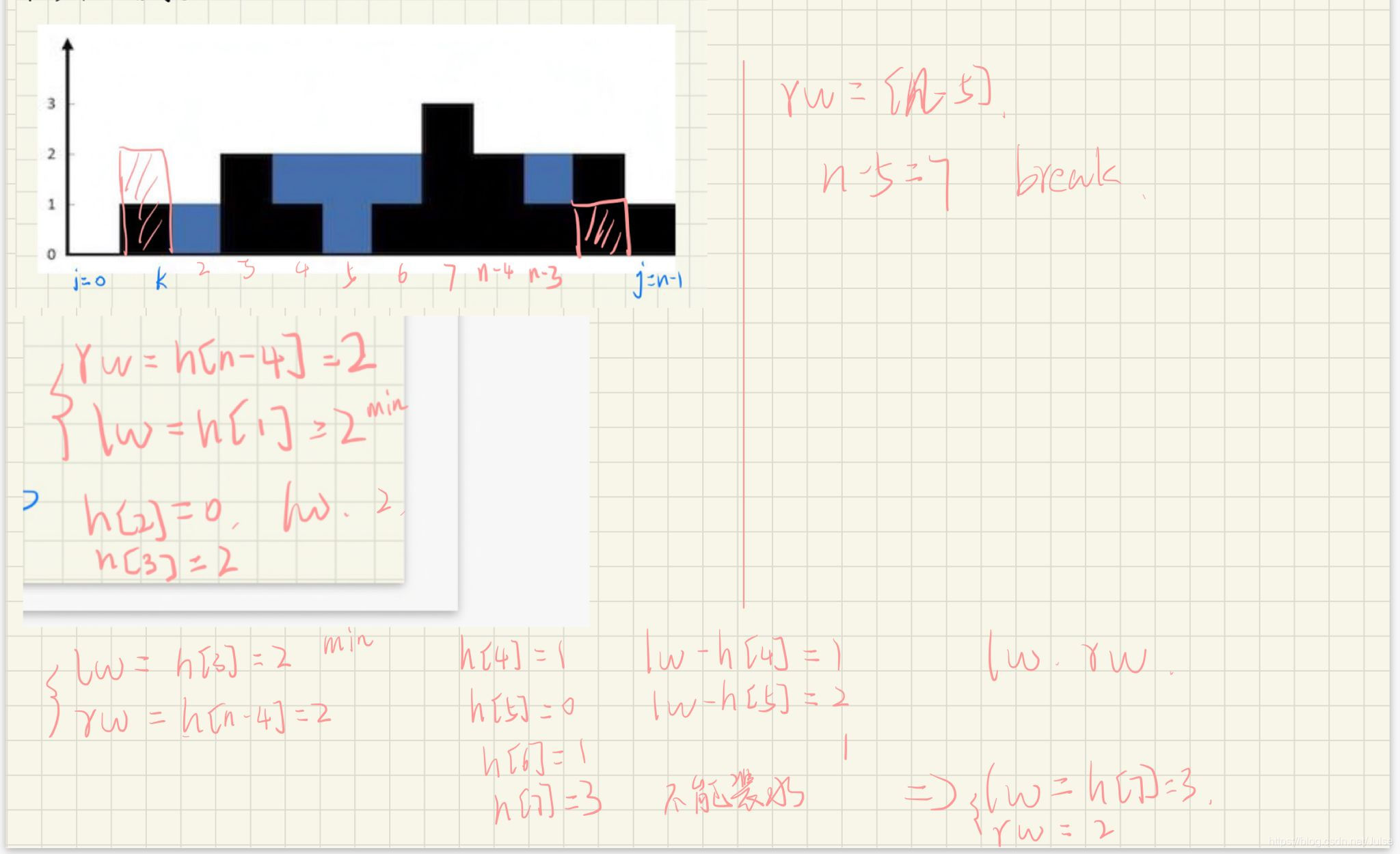
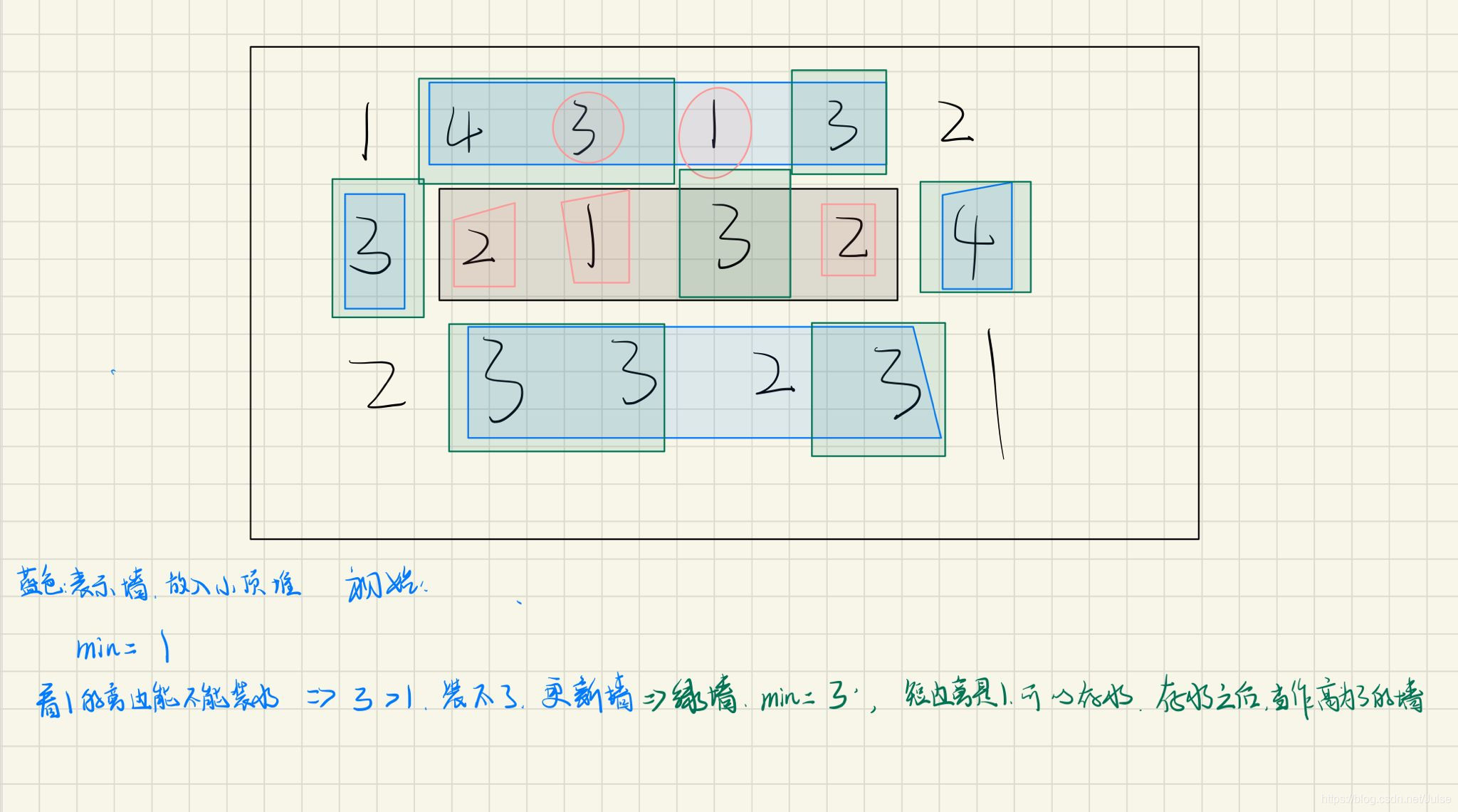

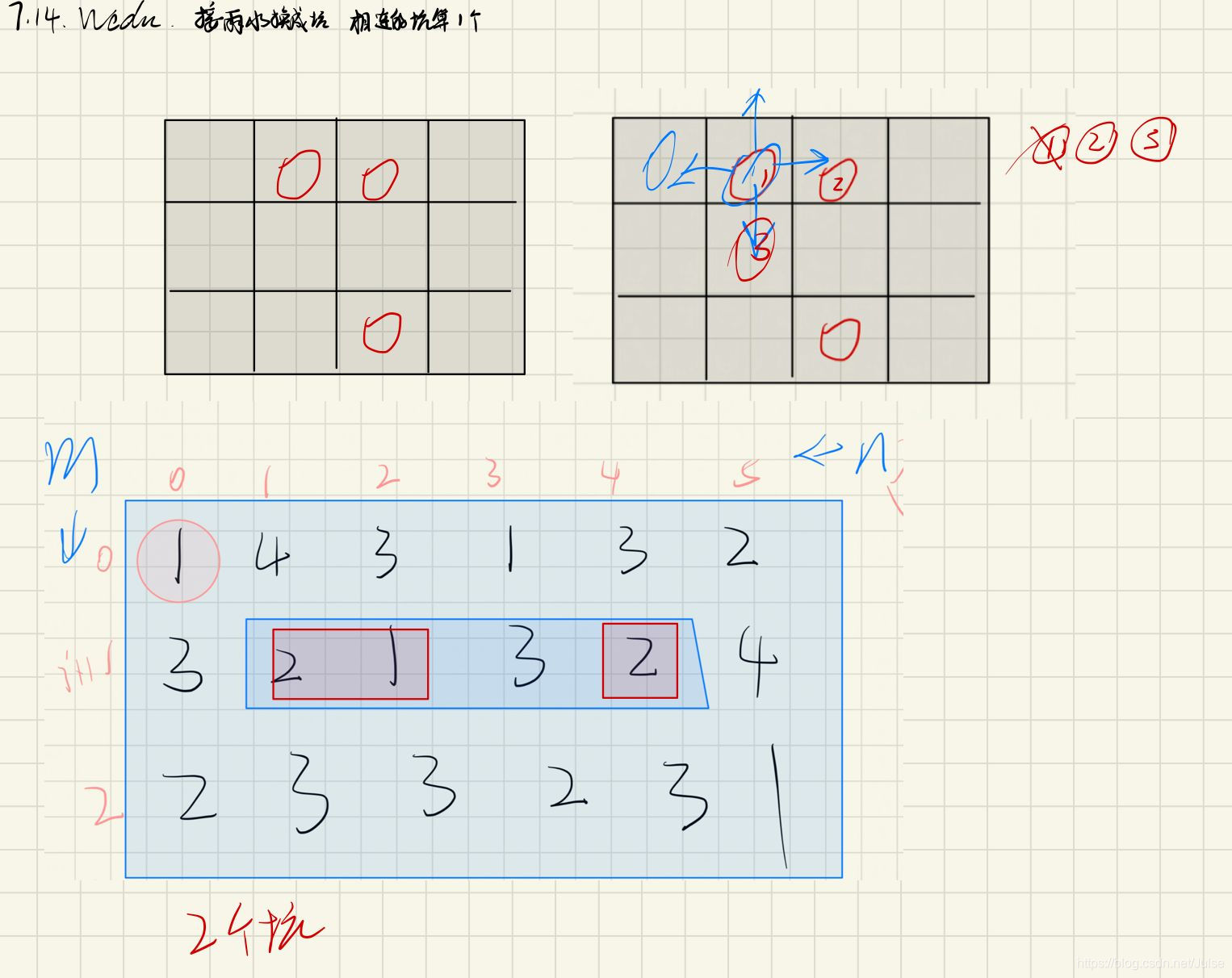








 本文介绍了LeetCode上的经典问题,如11. 容器接水和42. 接雨水的解决方案,包括双指针、找最矮墙等策略。同时,对407. 二维雨水问题进行了拓展,提出了求解坑的数目,并给出了广度优先和深度优先的搜索方法。文章提供了详细的代码实现和测试用例。
本文介绍了LeetCode上的经典问题,如11. 容器接水和42. 接雨水的解决方案,包括双指针、找最矮墙等策略。同时,对407. 二维雨水问题进行了拓展,提出了求解坑的数目,并给出了广度优先和深度优先的搜索方法。文章提供了详细的代码实现和测试用例。
















 1668
1668

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








