Binary Indexed Tree树状数组初步 & USACO2011 November Gold Above the Median

---

Description

Farmer John has lined up his $N$ (1$\le N \le$100,000) cows in a row to measure their heights; cow $i$ has height $H_i$ (1$\le H_i \le$1,000,000,000) nanometers–FJ believes in precise measurements! He wants to take a picture of some contiguous subsequence of the cows to submit to a bovine photography contest at the county fair.

The fair has a very strange rule about all submitted photos: a photograph is only valid to submit if it depicts a group of cows whose median height is at least a certain threshold $X$ (1$\le X \le$1,000,000,000).

For purposes of this problem, we define the median of an array A[0…K] to be A[$\lceil\frac{K}{2}\rceil$] after A is sorted. For example the median of {7, 3, 2, 6} is 6, and the median of {5, 4, 8} is 5.

Please help FJ count the number of different contiguous subsequences of his cows that he could potentially submit to the photography contest.

题目大意

给定一个序列，求有多少个区间满足其中的中位数（如果区间内元素个数n为偶数，则中位数为第n/2+1个）不小于给定值X。

Input

• Line 1: Two space-separated integers: N and X.
• Lines 2..N+1: Line i+1 contains the single integer H_i.

Sample Input

4 6
10
5
6
2

Output

• Line 1: The number of subsequences of FJ’s cows that have median at least X. Note this may not fit into a 32-bit integer.

Sample Output

7

---

$Solution$：
暴力$O(n^3)$的做法是枚举一维$O(n)$，滑动一维$O(n)$，用插入排序操作$O(n)$维护数组有序。但这样显然是过不了的，这个时候我们需要挖掘数据间的关系。

要注意的是题目是要求我们判断区间内中位数与给定值的大小关系，而不是具体得到所有符合题意的中位数的准确值。因而我们可以把每个数与给定值的关系用+-1表示出来，得到下面这个转化关系：如果一个区间内的总权值为非负的，则这个区间的中位数不小于给定的准确值。

这样我们就可以得到$O(n^2)$的做法：

• 枚举一维R $O(n)$，滑动一维L $O(n)$，找所有满足$\sum_{i=1}^{R}w[i]-\sum_{j=1}^{L-1}w[j] \ge 0$的L。

注意我们上述的说法，实际上我们只需要找到所有$\{sum[j]<=sum[i]\mid j \lt i\}$的j的个数即可。即维护一段权值区间内元素的个数。那么我们就可以采用数据结构来优化此题。

$1)$权值线段树

因为权值是可以$O(n)$预处理出来的，所以我们可以对权值进行离散，线段树维护权值$[1,sum[j]-1]$内的元素个数，每次再插入$sum[j]$即可。

$Code$：

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define M 100005
using namespace std;
int sum[M],n,P,res[M];
struct Weight{
    struct Node{
        int cnt;
        Node(){cnt=0;}
    }tree[M<<2];
    void update(int L,int R,int c,int p){
        if(L==R){
            tree[p].cnt++;
            return;
        }
        int mid=L+R>>1;
        if(c<=mid)update(L,mid,c,p<<1);
        else update(mid+1,R,c,p<<1|1);
        tree[p].cnt=tree[p<<1].cnt+tree[p<<1|1].cnt;
    }
    int query(int L,int R,int l,int r,int p){
        if(l>r)return 0;
        if(L==l&&R==r)return tree[p].cnt;
        int mid=L+R>>1;
        if(r<=mid)return query(L,mid,l,r,p<<1);
        else if(l>mid)return query(mid+1,R,l,r,p<<1|1);
        else return query(L,mid,l,mid,p<<1)+query(mid+1,R,mid+1,r,p<<1|1);
    }
}Tree;
int main(){
    scanf("%d %d",&n,&P);
    for(int i=1;i<=n;i++){
        int x;scanf("%d",&x);
        if(x>=P)sum[i]=sum[i-1]+1;
        else sum[i]=sum[i-1]-1;
        res[i]=sum[i];
    }
    sort(res+1,res+n+1);
    int rn=unique(res+1,res+n+1)-(res+1);

    long long ans=0;
    for(int i=1;i<=n;i++){
        sum[i]=lower_bound(res+1,res+rn+1,sum[i])-res;
        ans+=Tree.query(1,rn,1,sum[i],1);
        if(res[sum[i]]>=0)ans++;
        Tree.update(1,rn,sum[i],1);
    }
    cout<<ans<<endl;
    return 0;
}

---

树状数组的基本功能是动态前缀和，它的本质是经过简化的线段树，再采用位运算优化常数。

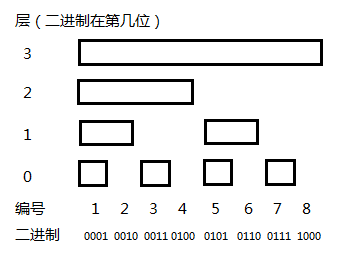
构建出的树状数组：

树状数组本质：

• 分析上述的权值线段树，我们可以发现：所有的右区间都是没有用的。因为一旦用到了整个右区间，那么我们可以直接使用包括它的上面那个大区间的值。为优化这类线段树，我们选择树状数组去代替。

树状数组复杂度：

• 没有预处理操作。
• 更新操作复杂度：$O(logn)$
• 求和操作复杂度：$O(logn)$

树状数组优势：

• 相较于线段树：
  
  • 更新和统计操作的常数比线段树小得多。（原因：线段树是严格的$O(logn)$，它要不断分治并且一直递归到底，而且由于递归操作也会导致变慢）
  • 所需空间比线段树小。
  • 代码短。w(ﾟДﾟ)w
• 相较于静态前缀和：
  
  • 在更新上静态前缀和更新不力，复杂度为$O(n)$。且树状数组有着更好的适用性。

树状数组劣势：

• 相较于线段树：
  
  • 不经过复杂实现的树状数组一般只能兼容查询区间连续和与前缀内最值（还必须要求更新是单调的，如LIS）的线段树。而线段树的一些更加灵活的运用则不好在树状数组上实现。

注意点：

• 树状数组非常依赖下标之间的关系，即编号一定要从1开始。在处理包含0下标的题目时要小心这一点，因为0是无法更新查询到的。

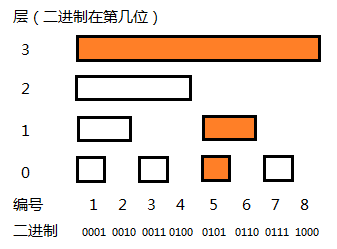
求值操作：

如果要计算$sum[7]$，我们提取出编号为4,6,7的节点就能完全覆盖$[1,7]$这段区间。

$$7_{10}=0111_{2}(7)=0110_2(6)+0001_2=0100_2(4)+0010_2+0001_2$$ 比较上述下标的关系，我们发现只需要每次除掉每个数 二进制下的最低位的1，就能找到所有覆盖 $sum[7]$的节点。

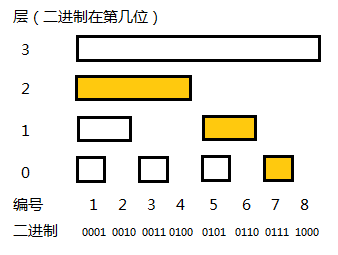
更新操作：

如果在位置5增加一个权值$\Delta a$，类比静态前缀和，我们需要更新所有的$sum[5,6,\ldots,n]$。所以我们需要将树状数组中覆盖它的5,6,8三个节点的值增加。

$$5_{10}=0101_{2}(5)=0110_2(6)-0001_2=1000_2(8)-0010_2-0001_2$$ 这里与求值时相反，需要每次加上每个数最低位的1即可。

查找最低位的1(lowbit)：x&(-x)

这个操作的正确性基于数在计算机中的存储方式。根据NOIP初赛知识点，计算机中所有的数都是以补码形式存在的。以x=6（用8位二进制表示）为例：

• x的补码：$00000110_2$（正数的原码，反码，补码全部相同）。
• -x的补码：$10000110_2$$\to$$11111001$$\to$$11111010$。

最后x&(-x)就是$00000010_2$了，也就是x的最低位的1。

---

$2)$树状数组（所以这是一道树状数组裸题）

$Code$：

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define M 100005
using namespace std;
int sum[M],n,P,res[M];
struct Binary_Indexed{
    int bit[M];
    inline void lowbit(int x){return x&(-x);}
    void add(int c){
        while(c<=n){
            bit[c]++;
            c+=lowbit(c);
        }
    }
    int query(int pos){
        int ans=0;
        while(pos>0){
            ans+=bit[pos];
            pos-=lowbit(pos); 
        }
        return ans;
    }
}Tree;
int main(){
    scanf("%d %d",&n,&P);
    for(int i=1;i<=n;i++){
        int x;
        scanf("%d",&x);
        x=(x>=P)?1:-1;
        sum[i]=sum[i-1]+x;
        res[i]=sum[i];
    }
    sort(res+1,res+n+1);
    int rn=unique(res+1,res+n+1)-(res+1);

    long long ans=0;
    for(int i=1;i<=n;i++){
        sum[i]=lower_bound(res+1,res+rn+1,sum[i])-res;
        ans+=Tree.query(sum[i]);
        if(res[sum[i]]>=0)ans++;//特判一下区间长度为1的情况
        Tree.add(sum[i]);
    }
    cout<<ans<<endl;
    return 0;
}

---