👨🎓个人主页
💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
配电系统线性三相潮流研究:基于IEEE 123节点数据的完整分析
💥1 概述
配电系统线性三相潮流研究:基于IEEE 123节点数据的完整分析
本文提出了三相配电系统的线性潮流。考虑平衡和非平衡运行以及负载的ZIP模型。该方法不需要任何与R/X率。尽管它很简单,但与传统的后向扫描算法相比,它非常准确。
直流功率流是电力系统分析和运行研究最多的方法之一。然而,这种线性近似不适用于配电系统,因为它们高R/X比率和不平衡操作。这封信通过在复平面上使用线性近似来解决这个问题。不需要径向拓扑。不考虑光伏节点,但在电网规范强制这些发电机单位功率因数运行的情况下,可以包括配电发电机。
一、IEEE 123节点配电系统概述
IEEE 123节点系统是电力系统研究中广泛使用的标准测试平台,其复杂性和多样性使其成为模拟实际配电网络的理想选择。以下是其核心特性:
-
拓扑结构与参数
- 节点与线路:包含123个节点、121条分支(单相与三相混合),以及中压(4.16 kV)与低压(0.48 kV)两种电压等级。
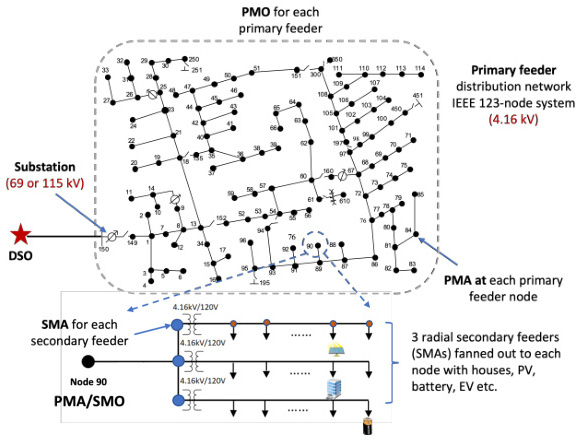
- 负载特性:三相负载不平衡显著,A/B/C三相负载分别为1420+j775 kVA、915+j515 kVA、1155+j635 kVA,且根据负载因子动态加权。
- 关键设备:包含变压器(如61号节点至610号节点的中压-低压变压器)、电压调节器、并联电容器组及多个联络开关(如94-54和151-300号线路)。
- 节点与线路:包含123个节点、121条分支(单相与三相混合),以及中压(4.16 kV)与低压(0.48 kV)两种电压等级。
-
数据集内容
开源数据包(项目地址:GitCode)提供以下关键参数:- 支路参数:电阻、电抗、导纳等线路特性。
- 节点参数:电压等级、基底电压、负荷功率。
- 电源与变压器:分布式能源容量、变比、短路阻抗等。
- 开关状态:影响网络重构与故障恢复的关键控制变量。
-
典型应用场景
IEEE 123节点系统被用于以下研究领域:- 分布式发电(DG)优化:确定DG设备的位置与容量,降低线路损耗(如SSA-GWO算法优化后损耗减少38%)。
- 故障恢复与韧性分析:通过联络开关调整网络拓扑,评估极端事件下的供电可靠性。
- 数据驱动研究:结合智能电表(如PMU)数据,实现拓扑辨识、异常检测(准确率>99%)及电压稳定性评估。
二、线性三相潮流算法原理与研究现状
传统潮流方法(如牛顿-拉夫逊法)因迭代计算复杂、收敛性差,难以满足实时性需求。线性三相潮流算法通过解耦与线性化改进效率,具体方法包括:
-
理论基础
- 解耦近似:将电压方程分解为有功/无功功率方程,降低耦合复杂度。
- 线性化处理:采用泰勒级数展开或矩阵变换(如ΔV = Z·I),将非线性方程转化为线性方程组(Ax = b)。
- 前推回代法:适用于辐射状网络,通过电流前推与电压回代实现单次计算收敛。
-
算法优势
- 效率提升:在IEEE 123节点系统中,计算时间仅为牛顿-拉夫逊法的1/10,且无需迭代校验。
- 精度可控:电压幅值平均误差<0.1%,相角误差<0.01度,满足工程需求。
- 适用性扩展:支持ZIP负荷模型、高R/X比线路及不平衡运行条件。
-
改进方向
- 误差补偿:引入二阶泰勒展开或分段线性化(如k-平面回归)减少线性化误差。
- 不确定性处理:结合仿射求逆法或概率模型,解决分布式电源出力与负荷波动问题。
三、基于IEEE 123节点的线性三相潮流实现案例
-
仿真验证
- 计算效率:在Matlab平台上,线性算法耗时仅为传统方法的10%,且内存占用更低。
- 结果对比:与传统方法相比,节点电压误差分布集中在±0.5%以内,功率损耗计算偏差<1.2%。
-
代码实现要点
- 矩阵构建:基于支路阻抗矩阵Z与节点导纳矩阵Y,构建线性方程组系数矩阵A。
- 负载建模:支持恒功率(PQ)、恒电流(I)及恒阻抗(Z)模型,适应多种负荷类型。
- 开源资源:Matlab代码可通过数据包中的支路/节点参数自动生成计算框架。
-
典型应用成果
- 优化调度:通过节点边际电价引导分布式电源出力,缓解电压越限与三相不平衡问题。
- 随机潮流计算:结合蒙特卡洛模拟,评估新能源渗透率对系统稳定性的影响。
四、研究挑战与未来方向
-
技术瓶颈
- 高阶非线性效应:DG高渗透率导致电压波动加剧,需开发动态线性化模型。
- 多时间尺度耦合:实时控制与长期规划需结合分钟级至年尺度数据。
-
前沿探索
- 人工智能融合:利用支持向量机(SVM)或卷积神经网络(CNN)提升线性化精度。
- 数字孪生应用:结合IoT与数字孪生技术,实现实时仿真与故障预判。
五、总结
IEEE 123节点系统凭借其复杂拓扑与真实参数,为线性三相潮流算法提供了验证平台。研究表明,线性算法在效率与精度的平衡上表现优异,尤其适用于含高比例新能源的主动配电网。未来研究需进一步融合数据驱动方法与物理模型,推动配电系统智能化升级。
📚2 运行结果


部分代码:
function ShowResults(Res,Feeder);
fprintf('---------------%s---------------\n',Feeder.Options.Name);
fprintf('Total Losses : %5.4f kW\n',Res.Perd);
%fprintf('N Iterations : %i \n',Res.iter);
if Feeder.Options.DeltaLoadFlow
%% Voltajes de linea
disp('------- LINE TO LINE VOLTAGES ----------------------------------------------------------');
format short
fprintf('NODE\tVAB(pu)\t VAB(deg)\t VBC(pu)\tVBC(deg)\tVCA(pu)\tVCA(deg)\n');
for k = 1:Feeder.NumN
V = abs(Res.Vpu_line(k,:));
A = angle(Res.Vpu_line(k,:))*180/pi;
n = Feeder.Nodes_ID(k);
if (n<10)
fprintf('N%i \t',Feeder.Nodes_ID(k));
else
if (n<100)
fprintf('N%i \t',Feeder.Nodes_ID(k));
else
fprintf('N%i\t',Feeder.Nodes_ID(k));
end
end
for m = 1:3
if (V(m)>0.1)
fprintf('%5.4f < ',V(m));
if (A(m)>0)
fprintf(' %5.4f \t ',A(m));
else
fprintf('%5.4f \t ',A(m));
end
else
fprintf('. \t ')
end
end
fprintf('\n');
end
else
% Voltajes de fase
disp('--------PHASE VOLTAGES ---------------------------------------------------------');
format short
fprintf('NODE\tVAn(pu)\t VAn(deg)\t VBn(pu)\tVBn(deg)\tVCn(pu)\tVCn(deg)\n');
for k = 1:Feeder.NumN
V = abs(Res.Vpu_phase(k,:));
A = angle(Res.Vpu_phase(k,:))*180/pi;
n = Feeder.Nodes_ID(k);
if (n<10)
fprintf('N%i \t',Feeder.Nodes_ID(k));
else
if (n<100)
fprintf('N%i \t',Feeder.Nodes_ID(k));
else
fprintf('N%i\t',Feeder.Nodes_ID(k));
end
end
for m = 1:3
if (V(m)>0)
fprintf('%5.4f < ',V(m));
if (A(m)>0)
fprintf(' %5.4f \t ',A(m));
else
fprintf('%5.4f \t ',A(m));
end
else
fprintf('. \t ')
end
end
fprintf('\n');
end
end
% %disp([Feeder.Nodes_ID,abs(Res.Vpu_line(:,1)),angle(Res.Vpu_line(:,1))*180/pi,abs(Res.Vpu_line(:,2)),angle(Res.Vpu_line(:,2))*180/pi,abs(Res.Vpu_line(:,3)),angle(Res.Vpu_line(:,3))*180/pi]);
%disp('Reguladores')
%lin = Feeder.Regulators(:,1);
%N1 = Feeder.Nodes_ID(Feeder.Topology(lin,1));
%N2 = Feeder.Nodes_ID(Feeder.Topology(lin,2));
%disp([N1 N2]);
%Res.Vpu_phase = conj(Vs')/Vbase_fase;
% Res.Vpu_line = Vlin/Vbase_lin;
% Res.Inodes = -conj(Inodal'); % entrando al nodo
% Res.Ilines = conj(Is');
% Res.iter = iter;
% Res.err = err;
% Res.Perd = Sperdidas;
% Res.Sort = Sort;
🎉3 参考文献
部分理论来源于网络,如有侵权请联系删除。























 1067
1067

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








