C++基础：tarjan算法

Keven_11

已于 2022-01-30 17:52:00 修改

阅读量1.7k

点赞数 11

分类专栏： C++基础知识文章标签： c++ 图论 tarjan

于 2022-01-29 22:56:52 首次发布

原文链接：https://www.jisuanke.com

版权

C++基础知识专栏收录该内容

50 篇文章

订阅专栏

本文详细介绍了图论中的割点、点双连通分量、桥和边双连通分量的概念，并提供了C++实现这些概念的算法。通过对无向图进行深度优先搜索，求解割点、点双连通分量以及桥，同时探讨了强连通分量的计算方法。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

一.割点和点双连通分量

1.割点

在一个 无向连通图 中，如果删除这个点和这个点关联的所有边，剩下图的连通分量大于 1，也即剩下的图不再连通，那么我们称这个点是割点。

比如对于下面这个图，割点有两个，分别是 1 和 3。这说明一个图可以有多个割点。

2.点双连通图（点双）

一个点双连通图的定义如下：一个 无向连通图 ，对于任意一个点，如果删除这个点和这个点关联的所有边，剩下的图还是连通的，那么称这个图是一个 点双连通图，也就是点双连通图中不会有割点出现。

下图是一个点双连通图。

3.点双连通分量（点双）

无向图 G 的的所有子图 G' 中，如果 G' 是一个点双连通图，则称图 G′ 为图 G 的点双连通子图。如果一个点双连通子图 G′ 不是任何一个点双连通子图的真子集，则图 G' 为图 G 的 极大点双连通子图，也称为 点双连通分量。

连通图与连通分量（连通块）的区别：https://mp.csdn.net/mp_blog/creation/editor/121315793

二.桥和边双连通分量

1.桥

在一个 无向连通图 中，如果删除某条边，剩下图的连通分量的个数大于 1，也即剩下的图不再连通，那么我们称这条边是桥。

下图中，用绿色标识的边是桥。

桥与割点的区别：桥针对于边，割点针对与点和与之关联的边。

2.边双连通图（边双）

一个边双连通图的定义如下：一个 无向连通图 ，对于任意一条边，如果删除这条边，剩下的图还是连通的，那么称这个图是一个 边双连通图，也就是边双连通图中不会有桥出现。

下图是一个边双连通图。

3.边双连通分量（边双）

无向图图 G 的的所有子图 G′ 中，如果 G′ 是一个边双连通图，则称图 G′ 为图 G 的 边双连通子图。如果一个边双连通子图 G′ 不是任何一个边双连通子图的真子集，则 G′ 为图 G 的 极大边双连通子图，也称为 边双连通分量。

点双连通和边双连通的区别，用下面这个图就可以很明显的看出来。下图是一个边双连通图，却不是一个点双连通图，它有两个点双连通分量，3 是割点。

4.强连通分量

前面我们一直都在讨论无向图的连通性，而避开有向图。因为有向图的连通性比较特殊，在有向图中，如果存在点 a 到 b 的路径，却不一定存在 b 到 a 路径。

如果 有向图 G 中任意两个点都 相互可达，则称图 G 是一个 强连通图。

下图是一个强连通图。

有向图 G 的的所有子图 G′ 中，如果 G′ 是一个强连通图，则称图 G′ 为图 G 的 强连通子图。如果一个强连通子图 G′ 不是任何一个强连通子图的真子集，则 G′ 为图 G 的 极大强连通子图，也称为 强连通分量。

二.连通性的理解

强连通图中必然存在环
一个点只可能属于一个边双连通分量（如果某个点属于两个边双连通分量，这两个边双连通分量可以合并成一个更大的边双连通分量）
点双连通图不一定是边双连通图（这个有两个点和一条边的图，是点双而不是边双）
边双连通图不一定是点双连通图（漏斗形）

三.求割点与点双连通分量

前面我们已经介绍了割点和点双连通分量的概念，这一节我们将重点关注如何求割点和点双连通分量。

在此之前，我们先介绍 时间戳 的概念，后面求其他几种连通分量都需要用到时间戳。

时间戳是对一个图做深度优先搜索的时候，第一次访问某个点的时间，初始时间为 0，每访问一个点，时间都加 1。反映在代码中如下，我们用dfn数组记录访问每个点的时间。

int times = 0;
int dfn[maxn];
void dfs(int u) {
    dfn[u] = ++times;
    for (int i = p[u]; i != -1; i = E[i].next) {
        int v = E[i].v;
        if (dfn[v] == 0) {
            dfs(v);
        }
    }
}

我们在图上做对每个点只访问一次的 DFS，虽然是在图上，但是实际上，会形成一颗搜索树。在从点 u 访问点 v 的时候，如果 v 之前没有被访问过，那么我们会对 v 继续做 DFS，这样，(u, v) 就是一条树边。如果 v 已经被访问，并且 v 是 u 的一个祖先，那么 (u, v)(u,v) 就是一条 反向边(返祖边)。

如下左图，以 AA 为根结点进行 DFS，右图中的实线表示树边，虚线表示反向边。数字标识时间戳。

基于前面基础，我们现在来求图的割点。为了简化讨论，我们假设整个图是一个连通图。对于树根来说，显而易见，当且仅当它有两个或者更多的子结点的时候，它才是割点。如下图，子树 1 和子树 2 之间不会不存在任何边，如果存在的话，子树 1 DFS 的时候就会访问了子树 2 的所有点，而不会由 u 去访问子树 2，那么去掉根结点以后，会形成两个连通块。

对于非根结点，就变得复杂，但是有如下定理。

定理：在无向连通图 G 的 DFS 树中，非根结点 u 是个割点当且仅当 u 存在一个子结点 v，使得 v 及其所有后代都没有反向边连回 u 的祖先（不包括 u）。

证明：如下图，考虑 uu 的任意子结点 v，如果 v 及其后代不能连回 f，则删除 u 之后，f 和 v 不再连通；反过来如果 v 或者它的某个后代存在一条反向边连回 f，则删除 u 之后，以 v 为根的整棵子树都能通过这条反向边和 f 连通。

有了前面的定理，我们用一个 low(u) 来表示 u 以及其后代 最多经过 一条反向边能回到的最早的点的时间戳。对于树边 (u,v) 当有一个 v 满足 low(v)≥dfn(u) 时，u 就是割点。

而更新 low(u) 就很简单了，对于树边 (u,v)，有 low(u)=min(low(u), low(v))，对于 反向边 (u, v)，有 low(u)=min(low(u),dfn(v))。当然，初始的时候，low(u)=dfn(u)，我们认为自己当然可以回到自己。

经过前面这么多的分析，我们就可以完全写出代码了。注意我们的代码中需要传入一个fa参数表示父节点。

int times = 0;
int dfn[maxn], low[maxn];
bool iscut[maxn];  // 标记是否是割点
void dfs (int u, int fa) {
    dfn[u] = low[u] = ++times;
    int child = 0;  // 用来处理根结点子结点数
    for (int i = p[u]; i != -1; i = E[i].next) {
        int v = E[i].en;
        if (dfn[v] == 0) {  // v 没有被访问过，u, v 是树边
            ++child;
            dfs(v, u);
            low[u] = min(low[u], low[v]);
            if (low[v] >= dfn[u]) {
                iscut[u] = true;
            }
        } else if (dfn[v] < dfn[u] && v != fa) {  // 反向边，注意 v == fa 的时候，是访问重复的边
            low[u] = min(low[u], dfn[v]);
        }
    }
    if (fa < 0 && child == 1) {
        // fa < 0 表示根结点，之前根结点一定会被标记为割点, 取消之
        iscut[u] = false;
    }
}

注意，调用上面的函数，初始fa参数必须传入一个负数，我们一般传入-1，比如dfs(1, -1)

求出了割点以后，我们再来求点双连通分量，求点双连通分量的算法如下:
用一个栈保存边，每次访问一个树边或者反向边的时候，把这条边压入栈中。当通过边 (u, v)(u,v) 找到一个割点 u 的时候，实际上就出现了一个点双连通分量，然后我们一直弹出栈中的边，直到弹出边 (u,v) 停止，这过程中弹出来的所有的边都属于同一个点双连通分量。

所以我们可以在 O(V+E) 的时间复杂度内求出割点和点双连通分量。

代码如下（没有处理重边，若要能处理重边，需要单独标记每条边是否被访问），这里，我们用set记录每个点双连通分量的点集。

int times = 0;
int dfn[maxn], low[maxn];
int bcc_cnt = 0;  // 点双连通分量数量
bool iscut[maxn];  // 标记是否是割点
set<int> bcc[maxn];  // 记录每个点双连通分量里面的点
stack<edge> S;
void dfs (int u, int fa) {
    dfn[u] = low[u] = ++times;
    int child = 0;  // 用来处理根结点子结点数
    for (int i = p[u]; i != -1; i = E[i].next) {
        int v = E[i].v;
        if (dfn[v] == 0) {  // v 没有被访问过，u, v 是树边
            S.push(E[i]);
            ++child;
            dfs(v, u);
            low[u] = min(low[u], low[v]);
            if (low[v] >= dfn[u]) {
                iscut[u] = true;
                ++bcc_cnt;  // 增加一个点双连通分量
                while (true) {
                    edge x = S.top();
                    S.pop();
                    bcc[bcc_cnt].insert(x.u);
                    bcc[bcc_cnt].insert(x.v);
                    if (x.u == u && x.v == v) {
                        break;
                    }
                }
            }
        } else if (dfn[v] < dfn[u] && v != fa) {  // 反向边，注意 v == fa 的时候，是访问重复的边
            S.push(E[i]);
            low[u] = min(low[u], dfn[v]);
        }
    }
    if (fa < 0 && child == 1) {
        // fa < 0 表示根结点，之前根结点一定被标记为割点, 取消之
        iscut[u] = false;
    }
}

我们以下面的图为例子跑一遍算法。

对 1 号点进行 dfs。

访问 (1,2) 这条边，对 2 做 dfs，并且把边压入栈中。

访问 (2,3) 这条边，对 3 做 dfs，并且把边压入栈中。

访问 (3,1) 这条边，dfn[1]<dfn[3]，这是一条反向边。更新 low[3]=1。

访问] (3,4) 这条边，对 4 做 dfs。

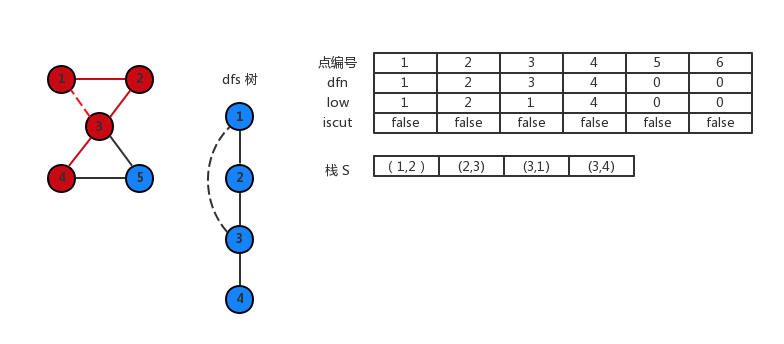
访问 (4,5) 这条边，对 5 做 dfs。

访问 (5,3) 这条边，是反向边。更新 low[5]=3。

没有边访问了，现在开始回溯了。由 5 回溯到 4 更新 4 的 low[4]=3。此时 low[5]<dfn[4]，没找到割点。

然后 4 回溯到 3，此时 low[4]≥dfn[3]，所以 3 是割点了，栈一直弹出边，直到弹出 (3,4) 这条边。得到 3,4,5 是一个点双连通分量。

继续回溯，直到 1，此时 low[2]≥dfn[1]，所以 1 被设置成为割点，栈一直弹出边，直到弹出 (1,2) 这条边。得到点 1,2,3 是一个双连通分量。

最后 1 回溯，由于根结点的特殊性，取消 1 是割点的标记。

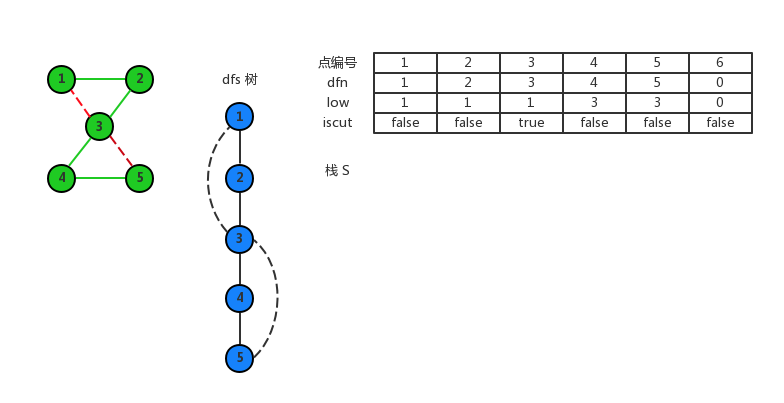
至此，算法结束，所有的割点和点双连通分量都求出来了。

总代码：

#include <iostream>
#include <stack>
#include <set>
#include <cstring>
using namespace std;
const int maxm = 1010;  // 最大边数
const int maxn = 110;  // 最大点数
struct edge {
    int u, v;
    int next;
} E[maxm];
int p[maxn], eid = 0;
void init() {
    memset(p, -1, sizeof(p));
    eid = 0;
}
void insert(int u, int v) {
    E[eid].u = u;
    E[eid].v = v;
    E[eid].next = p[u];
    p[u] = eid++;
}
int times=0;
int dfn[maxn],low[maxn];
int bcc_cnt=0;
bool iscut[maxn];
set<int> bcc[maxn];
stack<edge> S;
void dfs(int u,int fa){
    dfn[u]=low[u]=++times;
    int child=0;
    for (int i=p[u];i!=-1;i=E[i].next){
        int v=E[i].v;
        if (dfn[v]==0){
            S.push(E[i]);
            ++child;
            dfs(v,u);
            low[u]=min(low[u],low[v]);
            if (low[v]>=dfn[u]){
                iscut[u]=true;
                ++bcc_cnt;
                while (true){
                    edge x=S.top();
                    S.pop();
                    bcc[bcc_cnt].insert(x.u);
                    bcc[bcc_cnt].insert(x.v);
                    if (x.u==u && x.v==v){
                        break;
                    }
                }
            }
        }else if (dfn[v]<dfn[u] && v!=fa){
            S.push(E[i]);
            low[u]=min(low[u],dfn[v]);
        }
    }
    if (fa<0 && child==1){
        iscut[u]=false;
    }
}
int main() {
    init();
    int n, m;
    cin >> n >> m;
    for (int i = 0; i < m; ++i) {
        int u, v;
        cin >> u >> v;
        insert(u, v);
        insert(v, u);
    }
    memset(dfn, 0, sizeof(dfn));
    times = bcc_cnt = 0;
    dfs(1, -1);
    cout << bcc_cnt << endl;
    for (int i = 1; i <= bcc_cnt; ++i) {
        for (set<int>::iterator it = bcc[i].begin(); it != bcc[i].end(); ++it) {
            cout << (*it) << " ";
        }
        cout << endl;
    }
    return 0;
}

四.桥和边双连通分量

前面我们已经介绍了桥和边双连通分量的概念，这一节我们将重点关注如何求桥和边双连通分量。

求桥和边双连通分量还是会沿用之前求割点和点双连通的理论。

对于一条边 (u,v)，如果 v 及其后代结点能访问 u 及 u 之前，那么删掉边 (u,v) 之后，以 v 为根结点的子树和 u 能连通；反之，如果删除掉边 (u,v)，整个图就不连通了。所以一条边 (u, v) 是桥的条件是 low(v)>dfn(u)。

求边双连通分量和求点双连通分量的方法差不多，不同之处在于我们需要用栈来保存每个顶点而不是边。只需在dfs函数开头出把当前顶点 u 放入栈中，因为每个顶点只会进栈一次，我们只需用vector保存每个边双连通分量，而不需要用set。在dfs结尾，若low[u] == dfn[u]，有两种可能：

u 是根节点，此时我们需要把栈中的顶点弹出，放在一个新的双连通分量里。
u 不是根节点，说明low[u] > dfn[fa]，即fa→u 这条边为桥，我们需要把栈中的顶点弹出，直到 u 为止，然后把这些顶点放在一个新的双连通分量里。

核心代码如下（没有处理重边，若要能处理重边，需要单独标记每条边是否被访问），时间复杂度为 O(V+E)。

int times = 0;
int dfn[maxn], low[maxn];
int bcc_cnt = 0;        // 边双连通分量数量
vector<int> bcc[maxn];  // 记录每个点双连通分量里面的点
stack<int> S;
void dfs(int u, int fa) {
    dfn[u] = low[u] = ++times;
    S.push(u);
    for (int i = p[u]; i != -1; i = E[i].next) {
        int v = E[i].v;
        if (dfn[v] == 0) {  // v 没有被访问过，u, v 是树边
            dfs(v, u);
            low[u] = min(low[u], low[v]);
        } else if (dfn[v] < dfn[u] && v != fa) {  // 反向边，注意 v == fa 的时候，是访问重复的边
            low[u] = min(low[u], dfn[v]);
        }
    }
    if (low[u] == dfn[u]) {  // 此时 u 是根结点或者 fa -> u 是桥
        ++bcc_cnt;           // 增加一个边双连通分量
        while (!S.empty()) {  //从栈中弹出 u 及 u 之后的顶点
            int x = S.top();
            S.pop();
            bcc[bcc_cnt].push_back(x);
            if (x == u) break;  
        }
    }
}

总代码如下：

#include <cstring>
#include <iostream>
#include <stack>
#include <vector>
using namespace std;
const int maxm = 1010;  // 最大边数
const int maxn = 110;   // 最大点数
struct edge {
    int u, v;
    int next;
} E[maxm];
int p[maxn], eid = 0;
void init() {
    memset(p, -1, sizeof(p));
    eid = 0;
}
void insert(int u, int v) {
    E[eid].u = u;
    E[eid].v = v;
    E[eid].next = p[u];
    p[u] = eid++;
}
int times = 0;
int dfn[maxn], low[maxn];
int bcc_cnt = 0;
vector<int> bcc[maxn];
stack<int> S;
void dfs(int u, int fa) {
    dfn[u] = low[u] = ++times;
    S.push(u);
    for (int i=p[u];i!=-1;i=E[i].next){
        int v=E[i].v;
        if (dfn[v]==0){
            dfs(v,u);
            low[u]=min(low[u],low[v]);
        }else if (dfn[v]<dfn[u] && v!=fa){
            low[u]=min(low[u],dfn[v]);
        }
    }
    if (low[u] == dfn[u]) {
        ++bcc_cnt;
        while (true) {
            int x = S.top();
            S.pop();
            bcc[bcc_cnt].push_back(x);
            if (x == u) break;
        }
    }
}
int main() {
    init();
    int n, m;
    cin >> n >> m;
    for (int i = 0; i < m; ++i) {
        int u, v;
        cin >> u >> v;
        insert(u, v);
        insert(v, u);
    }
    memset(dfn, 0, sizeof(dfn));
    times = bcc_cnt = 0;
    dfs(1, -1);
    cout << bcc_cnt << endl;
    for (int i = 1; i <= bcc_cnt; ++i) {
        for (int j = 0; j < bcc[i].size(); j++) {
            cout << bcc[i][j] << " ";
        }
        cout << endl;
    }
    return 0;
}

五.求强连通分量

强连通分量是相对于有向图来说的。这一讲我们学习如何求强连通分量，求强连通分量的方法和之前学习的求双连通分量的方法有异曲同工之妙。

我们先考虑一个强连通分量 C，假设我们在 DFS 的时候，强连通分量中第一个被发现的点是 x，那么 C 中的其他点必然都是 x 的后代（强连通分量中任意两点相互可达）。那么如何找到每个强连通分量的第一个点呢？

如图，我们正在判断 u 是否为某个强连通分量的第一个被发现的点。如果我们发现从 u 的子结点出发可以到达 u 的某个祖先 w，那么 u,v,w 必然在同一个强连通分量里面，而 w 比 u 更早被发现，所以 w 才是第一个被发现的点，如上图 (a)。另外，如果从 v 最多只能发现到 u，那么 u 是这个强连通第一个发现的点。所以 u 是第一个被发现的点的条件是 low(u)=dfn(u)。

有了第一个被发现的点之后，我们还是借助栈来找强连通分量里面的点。每次对一个点做 dfs 的时候，都把这个点先压入到一个栈中（这里为什么只压入点？因为每个点只属于一个强连通分量）。当我们找到一个强连通分量的第一个点 u 的时候，栈中在这个点之后访问的点都和点 u 属于同一个强连通分量，具体的操作就是一直弹出栈顶元素，直到弹出来点 u。

这里有一个疑点，栈中 u 之后的元素一定是 u 的后代，但是为什么就一定和 u 是一个强连通分量呢？我们考虑，假如栈中 u 的后代中有一个点 v 和 u 不属于一个强连通分量，那么 v 势必应该之前会被当做另一个强连通分量的第一个点，所以 v 不应该出现在栈中的。

看下面的图就能理解了，假设我 dfs 的顺序为 A,B,C,D,E,F，那么 D 会被当做 D,E,F 这个强连通分量第一个被探测的点，而当回溯到 A 的时候，D,E,F 早已经出栈了，栈中只剩下 A,B,C 了。

还有一个需要处理的地方，这里处理的是有向图，不像连通无向图，连通无向图从任意点 dfs 都可以访问完所有点。但是，对于有向图，如果选择的点不对，就不能通过一次 dfs 访问所有的点。就如上一页这个图，

如果我们不幸的选择了 D 作为 dfs 的起点，那么只能求出来 D,E,F 这个强连通分量。要解决这个问题实际上很简单，我们对没有访问过的点都进行一次 dfs，每次 dfs 都能求出若干个强连通分量，把这些强连通分量在图上删掉以后，继续找其他的强连通分量。

这样，我们虽然可能进行了很多次 dfs，但是保证每个点只访问一次，最终总的时间复杂度是 O(V+E) 的。

代码：

#include <iostream>
#include <stack>
#include <set>
#include <cstring>
using namespace std;
const int maxm = 1010;
const int maxn = 110;
struct edge {
    int v;
    int next;
} E[maxm];
int p[maxn], eid = 0;
void init() {
    memset(p, -1, sizeof(p));
    eid = 0;
}
void insert(int u, int v) {
    E[eid].v = v;
    E[eid].next = p[u];
    p[u] = eid++;
}
int times = 0;
int dfn[maxn], low[maxn];
int scc_cnt = 0;  // 强连通分量数量
int sccno[maxn];  // 记录每个点属于的强连通分量的编号
set<int> scc[maxn];
stack<int> S;
void dfs (int u) {
    dfn[u] = low[u] = ++times;
    S.push(u);
    for (int i = p[u]; i != -1; i = E[i].next) {
        int v = E[i].v;
        if (dfn[v] == 0) {  // v 没有被访问过，u, v 是树边
            dfs(v);
            low[u] = min(low[u], low[v]);
        } else if (!sccno[v]) {  // 对于已经求出 scc 的点，直接删除
            low[u] = min(low[u], dfn[v]);
        }
    }
    if (low[u] == dfn[u]) {  // u 是第一个被探测到的点
        ++scc_cnt;
        while (true) {
            int x = S.top();
            S.pop();
            sccno[x] = scc_cnt;
            scc[scc_cnt].insert(x);
            if (x == u) {
                break;
            }
        }
    }
}
int main() {
    init();
    int n, m;
    cin >> n >> m;
    for (int i = 0; i < m; ++i) {
        int u, v;
        cin >> u >> v;
        insert(u, v);
    }
    memset(dfn, 0, sizeof(dfn));
    memset(sccno, 0, sizeof(sccno));
    times = scc_cnt = 0;
    for (int i = 1; i <= n; ++i) {
        if (!dfn[i]) {  // 每个点都要尝试 dfs 一次
            dfs(i);
        }
    }
    cout << scc_cnt << endl;
    for (int i = 1; i <= scc_cnt; ++i) {
        for (set<int>::iterator it = scc[i].begin(); it != scc[i].end(); ++it) {
            cout << (*it) << " ";
        }
        cout << endl;
    }
    return 0;
}

最后，我们通过一个例子来跑一遍求强连通的算法。

对于如下这个有向图，我们从顶点 0 开始进行 DFS。

将顶点 0 的 dfn0 和 low0 都设置为当前时间戳 1。

接下来访问相邻未访问的顶点 1，将 dfn1 和 low1 都设置为当前时间戳 22。

接下来访问相邻未访问顶点 3，将 dfn3 和 low3 都设置为当前时间戳 3。

没有其他相邻顶点，此时 dfn3=low3，故将 3 出栈作为一个强连通分量。

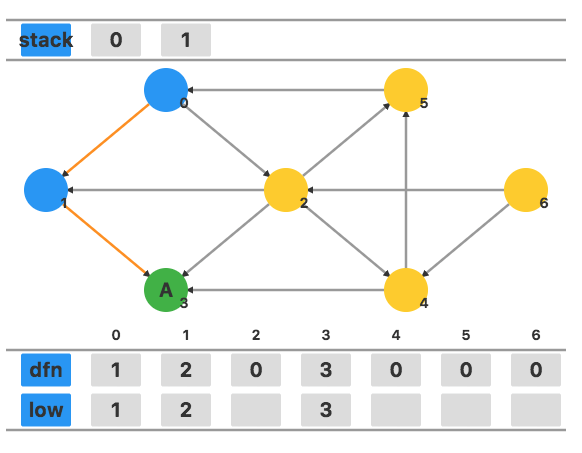
同样地，因为 dfn1=low1，所以将 1 出栈作为一个强连通分量。

继续访问和 0 相邻的其他顶点 2，将 dfn2 和 low2 都设置为当前的时间戳 4。

访问相邻顶点 4，将 dfn4 和 low4 都设置为当前的时间戳 5。

访问相邻顶点 5，将 dfn5 和 low5 都设置为当前的时间戳 6。

发现此时有指向栈中元素 1 的边，将 low5 更新为 dfn0=1。

回溯到顶点 4，用 low5 更新 low4，更新为 1。

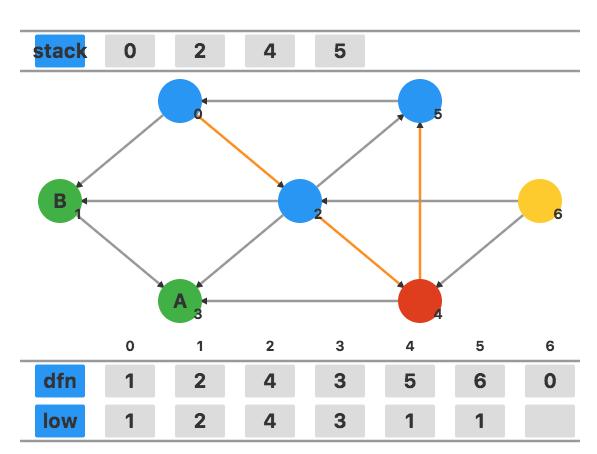
回溯到顶点 2，用 low4 更新 low2，更新为 1。

顶点 2 有一个在栈中的相邻顶点 5，用 dfn5 更新 low2，不发生任何变化。

回溯到顶点 0，用 low2 更新 low0。此时发现 low0=dfn0，将栈中元素弹出作为一个新的强连通分量。

找到下一个未访问的顶点 6，设置 dfn6=low6=7。

发现顶点 6 没有指向栈中元素的边，搜索结束，将 6 作为一个新的强连通分量。

计算结束，3,1,0,2,4,5,6 是图中的四个强连通分量。

六.缩点

以强连通分量为例

我们知道，一个强连通分量里面点，都是可以相互任意到达的，如果一个点能到达这个强连通分量里面的任一点，就可以到达这个强连通分量所有点。利用这一点，对于一些问题，可以把一个强连通分量里面的所有点看成是一个点，这也就是我们常说的缩点。

缩点以后会形成一个新的图，这个新图一定是一个 有向无环图，简写是 DAG，每个点代表一个强连通分量。

具体的操作方法如下，遍历原图上的每一条边，如果两个点不属于同一个强连通分量，然后在新图上的这两个强连通分量之间建一条有向边。

#include <iostream>
#include <stack>
#include <set>
#include <cstring>
using namespace std;
const int maxm = 1010;
const int maxn = 110;
struct edge {
    int v;
    int next;
} E[maxm];
int p[maxn], eid = 0;
void init() {
    memset(p, -1, sizeof(p));
    eid = 0;
}
void insert(int u, int v) {
    E[eid].v = v;
    E[eid].next = p[u];
    p[u] = eid++;
}
int times = 0;
int dfn[maxn], low[maxn];
int scc_cnt = 0;  // 强连通分量数量
int sccno[maxn];
set<int> scc[maxn];
stack<int> S;
void dfs (int u) {
    dfn[u] = low[u] = ++times;
    S.push(u);
    for (int i = p[u]; i != -1; i = E[i].next) {
        int v = E[i].v;
        if (dfn[v] == 0) {  // v 没有被访问过，u, v 是树边
            dfs(v);
            low[u] = min(low[u], low[v]);
        } else if (!sccno[v]) {  // 对于已经求出 scc 的点，直接删除
            low[u] = min(low[u], dfn[v]);
        }
    }
    if (low[u] == dfn[u]) {
        ++scc_cnt;
        while (true) {
            int x = S.top();
            S.pop();
            sccno[x] = scc_cnt;
            scc[scc_cnt].insert(x);
            if (x == u) {
                break;
            }
        }
    }
}
edge new_E[maxm];
int new_p[maxn], new_eid = 0;
void new_init() {
    memset(new_p, -1, sizeof(new_p));
    new_eid = 0;
}
void new_insert(int u, int v) {
    new_E[new_eid].v = v;
    new_E[new_eid].next = new_p[u];
    new_p[u] = new_eid++;
}
int main() {
    init();
    int n, m;
    cin >> n >> m;
    for (int i = 0; i < m; ++i) {
        int u, v;
        cin >> u >> v;
        insert(u, v);
    }
    memset(dfn, 0, sizeof(dfn));
    times = scc_cnt = 0;
    for (int i = 1; i <= n; ++i) {
        if (!dfn[i]) {
            dfs(i);
        }
    }
    new_init();
    for (int u = 1; u <= n; ++u) {
        for (int i = p[u]; i != -1; i = E[i].next) {
            int v = E[i].v;
            if (sccno[u] != sccno[v]) {
                new_insert(sccno[u], sccno[v]);
            }
        }
    }
    return 0;
}