数学规划运输问题

最新推荐文章于 2024-04-18 19:58:00 发布

Kilig*

最新推荐文章于 2024-04-18 19:58:00 发布

阅读量1.8k

点赞数 2

分类专栏：数学建模文章标签：最优化模型运输问题线性规划 CVXPY 距离计算

本文链接：https://blog.csdn.net/Kilig___/article/details/119616002

版权

数学建模专栏收录该内容

18 篇文章

订阅专栏

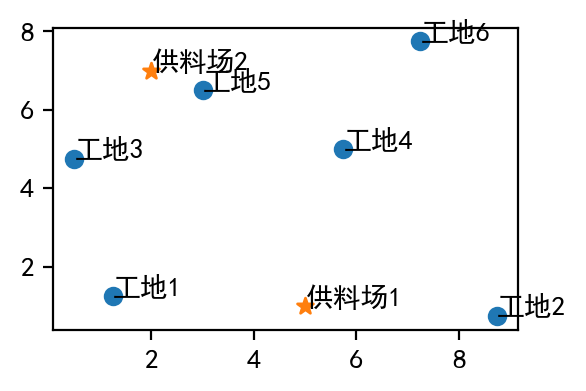
在这里插入图片描述
我们可以先绘制出各个工地以及临时料场的位置如下图所示

import numpy as np
import  matplotlib
import  matplotlib.pyplot as plt
#指定默认字体
matplotlib.rcParams['font.sans-serif'] = ['SimHei'] 
matplotlib.rcParams['font.family']='sans-serif'
#解决负号'-'显示为方块的问题
matplotlib.rcParams['axes.unicode_minus'] = False 

x = [1.25,8.75,0.5,5.75,3,7.25]
y = [1.25,0.75,4.75,5,6.5,7.75]
d = [3,5,4,7,6,11]
x_1 = [5,2]
y_1 = [1,7]
plt.figure(figsize=(3,2), dpi=200)
plt.scatter(x,y,marker="o")
plt.scatter(x_1,y_1,marker="*")
for i in range(1,7):
    plt.annotate("工地"+str(i),(x[i-1],y[i-1]))
    
for i in range(1,3):
    plt.annotate("供料场"+str(i),(x_1[i-1],y_1[i-1]))
plt.show()

我们可以算出供料场到各个工地的距离

第一个料场到各工地的距离[3.758324094593227, 3.758324094593227, 5.8576872569299905, 4.0697051490249265, 5.852349955359813, 7.115124735378854]
第二个料场到各工地的距离[5.798706752371601, 9.199184746487049, 2.704163456597992, 4.25, 1.118033988749895, 5.303300858899107]

x = [1.25,8.75,0.5,5.75,3,7.25]
y = [1.25,0.75,4.75,5,6.5,7.75]
d = [3,5,4,7,6,11]
x_1 = [5,2]
y_1 = [1,7]
def distance(x_1,y_1,x_2,y_2):
    return ((x_1-x_2)**2+(y_1-y_2)**2)**(1/2)
list_all = []
for i in range(2):
    list_line = []
    for j in range(6):
        list_line.append(distance(x_1[i],y_1[i],x[j],y[j]))
    list_all.append(list_line)
for i in list_all:
    print(i)

那么我们可以假设从第 $i$ 个料场运送往第 $j$ 个工地的水泥量为 $x_{ij}$ 距离为 $distance_{ij}$ 第 $j$ 个工地的水泥需求量为 $need_j$
那么我们可以建立模型:
$\qquad \sum_{i=1,j=1}^{i=2,j=6}x_{ij}*distance_{ij}$
$S.T.\left\{ \begin{aligned} \sum_{i=1}^{i=2}x_{ij}<=20\\ \sum_{j=1}^{j=6}x_{ij}>=need_j\\ x_{ij}>=0 \qquad,i=1,2\quad j= 1\cdots6 \end{aligned} \right.$
最终解得结果如下

import cvxpy as cp
import numpy as np
c=np.array(list_all)
x = cp.Variable((2,6),integer=False)
obj = cp.Minimize(cp.sum(cp.multiply(c,x)))
d = [3.,5.,4,7,6,11]
con= [cp.sum(x, axis=1, keepdims=True)<=np.array([20,20]).reshape(-1,1),
      cp.sum(x, axis=0, keepdims=True)==np.array([d]),
     x>=0]
prob = cp.Problem(obj, con)
prob.solve(solver='GLPK_MI',verbose =True)
print("最优值为:",prob.value)
print("最优解为：\n",x.value)
'''
输出结果
===============================================================================
                                     CVXPY                                     
                                    v1.1.12                                    
===============================================================================
(CVXPY) Aug 12 09:22:59 AM: Your problem has 12 variables, 3 constraints, and 0 parameters.
(CVXPY) Aug 12 09:22:59 AM: It is compliant with the following grammars: DCP, DQCP
(CVXPY) Aug 12 09:22:59 AM: (If you need to solve this problem multiple times, but with different data, consider using parameters.)
(CVXPY) Aug 12 09:22:59 AM: CVXPY will first compile your problem; then, it will invoke a numerical solver to obtain a solution.
-------------------------------------------------------------------------------
                                  Compilation                                  
-------------------------------------------------------------------------------
(CVXPY) Aug 12 09:22:59 AM: Compiling problem (target solver=GLPK_MI).
(CVXPY) Aug 12 09:22:59 AM: Reduction chain: Dcp2Cone -> CvxAttr2Constr -> ConeMatrixStuffing -> GLPK_MI
(CVXPY) Aug 12 09:22:59 AM: Applying reduction Dcp2Cone
(CVXPY) Aug 12 09:22:59 AM: Applying reduction CvxAttr2Constr
(CVXPY) Aug 12 09:22:59 AM: Applying reduction ConeMatrixStuffing
(CVXPY) Aug 12 09:22:59 AM: Applying reduction GLPK_MI
(CVXPY) Aug 12 09:22:59 AM: Finished problem compilation (took 1.900e-02 seconds).
-------------------------------------------------------------------------------
                                Numerical solver                               
-------------------------------------------------------------------------------
(CVXPY) Aug 12 09:22:59 AM: Invoking solver GLPK_MI  to obtain a solution.
-------------------------------------------------------------------------------
                                    Summary                                    
-------------------------------------------------------------------------------
(CVXPY) Aug 12 09:22:59 AM: Problem status: optimal
(CVXPY) Aug 12 09:22:59 AM: Optimal value: 1.362e+02
(CVXPY) Aug 12 09:22:59 AM: Compilation took 1.900e-02 seconds
(CVXPY) Aug 12 09:22:59 AM: Solver (including time spent in interface) took 5.996e-03 seconds
最优值为: 136.22751988318157
最优解为：
 [[ 3.  5. -0.  7. -0.  1.]
 [-0. -0.  4. -0.  6. 10.]]

'''