数值分析原理课程实验——牛顿（Newton）迭代法

牛顿（Newton）迭代法

方法概要

待求问题

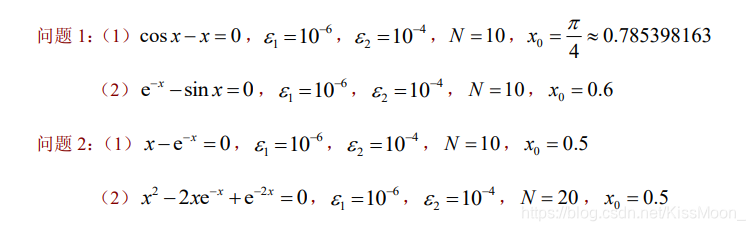
程序流程

程序代码

/*Matlab函数
function Result = Newton(x0, e1, e2, N, f)
    n = 1;
    while n <= N
        F = subs(f, symvar(f), x0);
        DF = subs(diff(f), symvar(f), x0);
        if(abs(F) < e1)
            Result = double(x0);
            return;
        end
        if(abs(DF) < e2)
            Result = 'Iteration failed!';
            return;
        end
        x1 = x0-F/DF;
        Tol = abs(x1 - x0);
        if(Tol < e1)
            Result = double(x1);
            return;
        end
        n = n+1;
        x0 = x1;
    end
    Result = 'Iteration failed!';
end*/


/*C语言程序
#include <stdio.h>
#include <stdlib.h>
#include <math.h>

double x, e1, e2;
int n;

double f(double x) { return cos(x) - x; }
double df(double x) { return -sin(x) - 1; }

int main() {
    scanf("%lf%lf%lf%d", &x, &e1, &e2, &n);
    for (int i = 1; i <= n; i++) {
        double F = f(x), DF = df(x);
        if (fabs(F) < e1) {
            printf("%lf", x);
            return 0;
        }
        if (fabs(DF) < e2) {
            printf("Failed");
            return 0;
        }
        double x1 = x - F / DF;
        double tol = fabs(x - x1);
        if (tol < e1) {
            printf("%lf", x1);
            return 0;
        }
        x = x1;
    }
    printf("Failed");
    return 0;
}
*/

运行结果

高斯（Gauss）列主元消去法，原文链接：

https://blog.csdn.net/KissMoon_/article/details/116278197

拉格朗日（Lagrange）插值，原文链接：

https://blog.csdn.net/KissMoon_/article/details/116278449

四阶龙格-库塔（Runge-Kutta）方法，原文链接：

https://blog.csdn.net/KissMoon_/article/details/116278567

Newton/Gauss/Lagrange/Runge-Kutta实验内容+方法指导+Matlab脚本+Matlab函数+Matlab运行报告+C程序+实验报告，一键下载：

https://download.csdn.net/download/KissMoon_/18244419

凉梦空间

欢迎你进入我的个人博客网站参观交流：https://www.liangmeng.xyz