Logistic回归模型、损失函数和成本函数
logistic模型
logistic模型： y ^ = σ ( w T x + b ) \hat{y} = σ(w^Tx+b) y^=σ(wTx+b) ； σ ( z ) = 1 1 + e − z σ(z)=\frac{1}{1+e^{-z}} σ(z)=1+e−z1，其中 w T x + b = z w^Tx+b=z wTx+b=z，所以 0 ≤ y ^ ≤ 1 0≤\hat{y}≤1 0≤y^≤1
损失函数
损失函数是在单个训练样本中定义的 ，它是衡量单个训练样本上的表现；
损失函数也叫误差函数，可以用来衡量算法的运行情况，损失函数越小，算法越精确；
如果使用 L ( y ^ , y ) = 1 2 ( y ^ − y ) 2 L(\hat{y},y)=\frac{1}{2}{(\hat{y}-y)}^2 L(y^,y)=21(y^−y)2，那么梯度下降法将不能使用；
因此使用 L ( y ^ , y ) = − ( y l o g y ^ + ( 1 − y ) l o g ( 1 − y ^ ) ) L(\hat{y},y)=-(ylog\hat{y}+(1-y)log(1-\hat{y})) L(y^,y)=−(ylogy^+(1−y)log(1−y^))，其中0＜ y ^ \hat{y} y^＜1;
如果训练样本 y = 1 y=1 y=1：那么 L ( y ^ , y ) = − l o g y ^ L(\hat{y},y)=-log\hat{y} L(y^,y)=−logy^，要使 L ( y ^ , y ) L(\hat{y},y) L(y^,y)足够小，就要 l o g y ^ log\hat{y} logy^足够大，就要 y ^ \hat{y} y^足够大（但是 y ^ \hat{y} y^永远＜1，即无限接近1）；
如果训练样本 y = 0 y=0 y=0：那么 L ( y ^ , y ) = − l o g ( 1 − y ^ ) L(\hat{y},y)=-log(1-\hat{y}) L(y^,y)=−log(1−y^)，要使 L ( y ^ , y ) L(\hat{y},y) L(y^,y)足够小，就要 l o g ( 1 − y ^ ) log(1-\hat{y}) log(1−y^)足够大，就要 y ^ \hat{y} y^足够小（但是 y ^ \hat{y} y^永远＞0，即无限接近0）；
总结：如果 y = 1 y=1 y=1，尽可能让 y ^ \hat{y} y^接近1；如果 y = 0 y=0 y=0，尽可能让 y ^ \hat{y} y^接近0。
成本函数
w和b的函数，衡量全体训练样本上参数w和b的效果的表现（成本函数越小越好）；
1 m \frac{1}{m} m1的损失函数之和的平均值
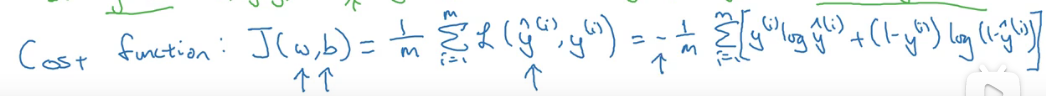
梯度下降法
来训练或学习训练集的参数w和b；
- 损失函数就是将训练出来的 y ^ ( i ) \hat{y}^{(i)} y^(i)和真值 y ( i ) y^{(i)} y(i)进行比较；
- 成本函数衡量了参数
w
w
w和
b
b
b在训练集上的效果，要训练出合适的
w
w
w和
b
b
b使得成本函数最小。
$J(w,b)是如上的凸函数
下图是用二维来解释梯度下降法的实现原理
①是斜率，通常只有一个变量用
d
d
d表示，两个变量以上用
∂
∂
∂表示，通常④表达是对的，但是③易理解，且通常使用②变量符号来代表①；
左上角的函数图解读：若 w w w在最低点的右边，则成本函数较大，通过减去 σ ∗ d ( w , b ) σ*d(w,b) σ∗d(w,b)（此时 d ( w , b ) d(w,b) d(w,b)为正），不断迭代使得 w w w减小（ b b b同理）最后找到最小的成本函数
121
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
