吴恩达Coursera课程 DeepLearning.ai 编程作业系列,本文为《神经网络与深度学习》部分的第四周“深层神经网络”的课程作业,增加了一些辅助的测试函数。
另外,本节课程笔记在此:《吴恩达Coursera深度学习课程 DeepLearning.ai 提炼笔记(1-4)》,如有任何建议和问题,欢迎留言。
Part 1:Building your Deep Neural Network: Step by Step
1 - Packages
Let’s first import all the packages that you will need during this assignment.
- numpy is the main package for scientific computing with Python.
- matplotlib is a library to plot graphs in Python.
- dnn_utils provides some necessary functions for this notebook.
- testCases provides some test cases to assess the correctness of your functions
- np.random.seed(1) is used to keep all the random function calls consistent. It will help us grade your work. Please don’t change the seed.
import numpy as np
import h5py
import matplotlib.pyplot as plt
from testCases_v3 import *
from dnn_utils_v2 import sigmoid, sigmoid_backward, relu, relu_backward
%matplotlib inline
plt.rcParams['figure.figsize'] = (5.0, 4.0) # set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'
%load_ext autoreload
%autoreload 2
np.random.seed(1)You can get the support code from here.
the sigmoid function:
def sigmoid(Z):
"""
Implements the sigmoid activation in numpy
Arguments:
Z -- numpy array of any shape
Returns:
A -- output of sigmoid(z), same shape as Z
cache -- returns Z as well, useful during backpropagation
"""
A = 1/(1+np.exp(-Z))
cache = Z
return A, cachethe sigmoid_backward function:
def sigmoid_backward(dA, cache):
"""
Implement the backward propagation for a single SIGMOID unit.
Arguments:
dA -- post-activation gradient, of any shape
cache -- 'Z' where we store for computing backward propagation efficiently
Returns:
dZ -- Gradient of the cost with respect to Z
"""
Z = cache
s = 1/(1+np.exp(-Z))
dZ = dA * s * (1-s)
assert (dZ.shape == Z.shape)
return dZthe relu function:
def relu(Z):
"""
Implement the RELU function.
Arguments:
Z -- Output of the linear layer, of any shape
Returns:
A -- Post-activation parameter, of the same shape as Z
cache -- a python dictionary containing "A" ; stored for computing the backward pass efficiently
"""
A = np.maximum(0,Z)
assert(A.shape == Z.shape)
cache = Z
return A, cachethe relu_backward function:
def relu_backward(dA, cache):
"""
Implement the backward propagation for a single RELU unit.
Arguments:
dA -- post-activation gradient, of any shape
cache -- 'Z' where we store for computing backward propagation efficiently
Returns:
dZ -- Gradient of the cost with respect to Z
"""
Z = cache
dZ = np.array(dA, copy=True) # just converting dz to a correct object.
# When z <= 0, you should set dz to 0 as well.
dZ[Z <= 0] = 0
assert (dZ.shape == Z.shape)
return dZ2 - Outline of the Assignment
To build your neural network, you will be implementing several “helper functions”. These helper functions will be used in the next assignment to build a two-layer neural network and an L-layer neural network. Each small helper function you will implement will have detailed instructions that will walk you through the necessary steps. Here is an outline of this assignment, you will:
- Initialize the parameters for a two-layer network and for an L L -layer neural network.
- Implement the forward propagation module (shown in purple in the figure below).
- Complete the LINEAR part of a layer’s forward propagation step (resulting in ).
- We give you the ACTIVATION function (relu/sigmoid).
- Combine the previous two steps into a new [LINEAR->ACTIVATION] forward function.
- Stack the [LINEAR->RELU] forward function L-1 time (for layers 1 through L-1) and add a [LINEAR->SIGMOID] at the end (for the final layer L L ). This gives you a new L_model_forward function.
- Compute the loss.
- Implement the backward propagation module (denoted in red in the figure below).
- Complete the LINEAR part of a layer’s backward propagation step.
- We give you the gradient of the ACTIVATE function (relu_backward/sigmoid_backward)
- Combine the previous two steps into a new [LINEAR->ACTIVATION] backward function.
- Stack [LINEAR->RELU] backward L-1 times and add [LINEAR->SIGMOID] backward in a new L_model_backward function
- Finally update the parameters.
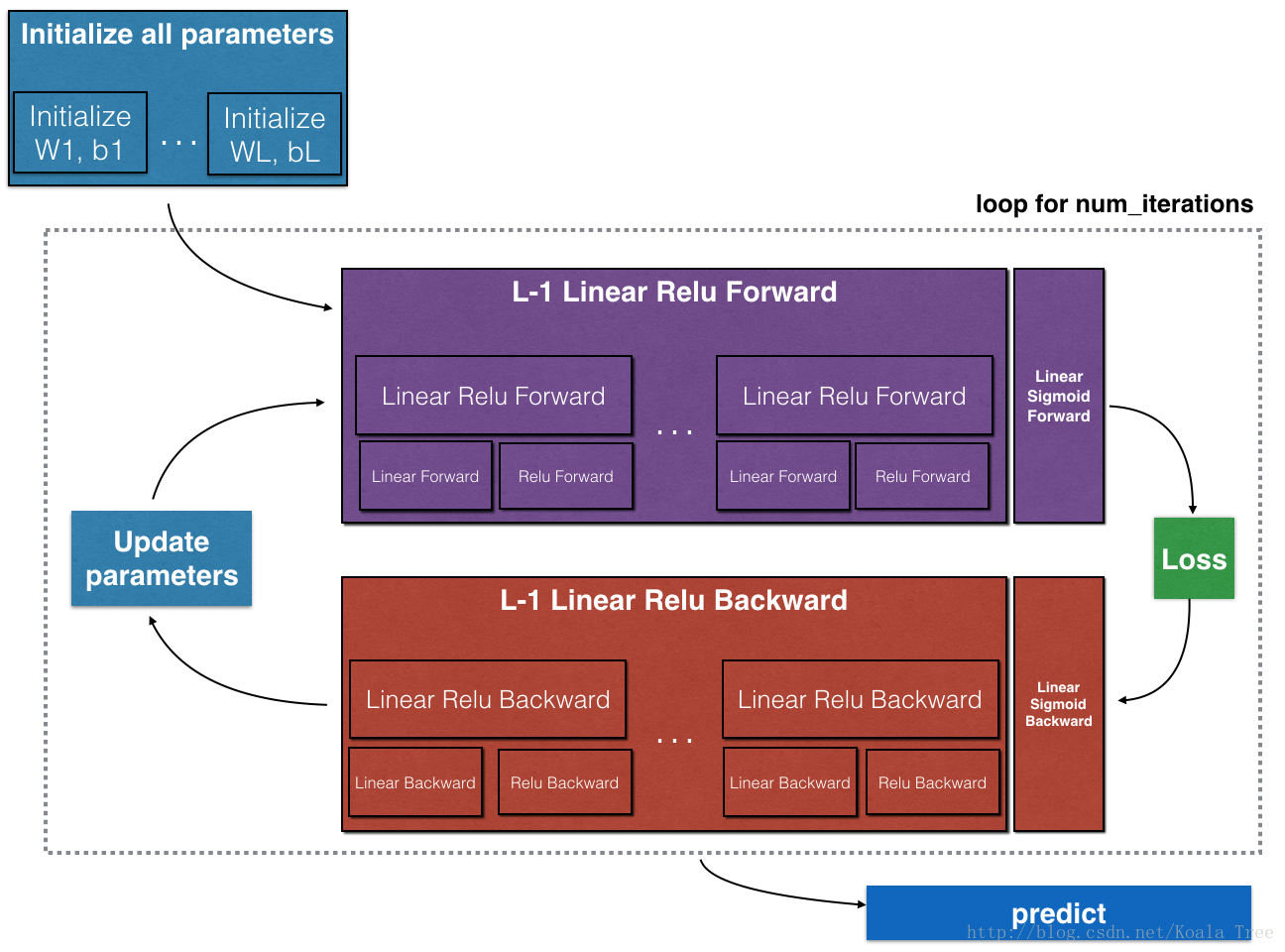
Note that for every forward function, there is a corresponding backward function. That is why at every step of your forward module you will be storing some values in a cache. The cached values are useful for computing gradients. In the backpropagation module you will then use the cache to calculate the gradients. This assignment will show you exactly how to carry out each of these steps.
3 - Initialization
You will write two helper functions that will initialize the parameters for your model. The first function will be used to initialize parameters for a two layer model. The second one will generalize this initialization process to layers.
3.1 - 2-layer Neural Network
Exercise: Create and initialize the parameters of the 2-layer neural network.
Instructions:
- The model’s structure is: LINEAR -> RELU -> LINEAR -> SIGMOID.
- Use random initialization for the weight matrices. Use np.random.randn(shape)*0.01 with the correct shape.
- Use zero initialization for the biases. Use np.zeros(shape).
# GRADED FUNCTION: initialize_parameters
def initialize_parameters(n_x, n_h, n_y):
"""
Argument:
n_x -- size of the input layer
n_h -- size of the hidden layer
n_y -- size of the output layer
Returns:
parameters -- python dictionary containing your parameters:
W1 -- weight matrix of shape (n_h, n_x)
b1 -- bias vector of shape (n_h, 1)
W2 -- weight matrix of shape (n_y, n_h)
b2 -- bias vector of shape (n_y, 1)
"""
np.random.seed(1)
### START CODE HERE ### (≈ 4 lines of code)
W1 = np.random.randn(n_h, n_x)*0.01
b1 = np.zeros((n_h, 1))
W2 = np.random.randn(n_y, n_h)*0.01
b2 = np.zeros((n_y, 1))
### END CODE HERE ###
assert(W1.shape == (n_h, n_x))
assert(b1.shape == (n_h, 1))
assert(W2.shape == (n_y, n_h))
assert(b2.shape == (n_y, 1))
parameters = {
"W1": W1,
"b1": b1,
"W2": W2,
"b2": b2}
return parameters parameters = initialize_parameters(3,2,1)
print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))W1 = [[ 0.01624345 -0.00611756 -0.00528172]
[-0.01072969 0.00865408 -0.02301539]]
b1 = [[ 0.]
[ 0.]]
W2 = [[ 0.01744812 -0.00761207]]
b2 = [[ 0.]]
3.2 - L-layer Neural Network
The initialization for a deeper L-layer neural network is more complicated because there are many more weight matrices and bias vectors. When completing the initialize_parameters_deep, you should make sure that your dimensions match between each layer. Recall that n[l] n [ l ] is the number of units in layer l l . Thus for example if the size of our input
is (12288,209) ( 12288 , 209 ) (with m=209 m = 209 examples) then:
| **Shape of W** | **Shape of b** | **Activation** | **Shape of Activation** | |
| **Layer 1** | (n[1],12288) ( n [ 1 ] , 12288 ) | (n[1],1) ( n [ 1 ] , 1 ) | Z[1]=W[1]X+b[1] Z [ 1 ] = W [ 1 ] X + b [ 1 ] | (n[1],209) ( n [ 1 ] , 209 ) |
| **Layer 2** | (n[2],n[1]) ( n [ 2 ] , n [ 1 ] ) | (n[2],1) ( n [ 2 ] , 1 ) | Z[2]=W[2]A[1]+b[2] Z [ 2 ] = W [ 2 ] A [ 1 ] + b [ 2 ] | (n[2],209) ( n [ 2 ] , 209 ) |
| ⋮ ⋮ | ⋮ ⋮ | ⋮ ⋮ | ⋮ ⋮ | ⋮ ⋮ |
| **Layer L-1** | (n[L−1],n[L−2]) ( n [ L − 1 ] , n [ L − 2 ] ) | (n[L−1],1) ( n [ L − 1 ] , 1 ) | Z[L−1]=W[L−1]A[L−2]+b[L−1] Z [ L − 1 ] = W [ L − 1 ] A [ L − 2 ] + b [ L − 1 ] | (n[L−1],209) ( n [ L − 1 ] , 209 ) |
| **Layer L** | (n[L],n[L−1]) ( n [ L ] , n [ L − 1 ] ) | (n[L],1) ( n [ L ] , 1 ) | Z[L]=W[L]A[L−1]+b[L] Z [ L ] = W [ L ] A [ L − 1 ] + b [ L ] | (n[L],209) ( n [ L ] , 209 ) |
Remember that when we compute WX+b W X + b in python, it carries out broadcasting. For example, if:








 本文详细介绍了吴恩达在Coursera上的深度学习课程《神经网络与深度学习》的编程作业,包括搭建深度神经网络的步骤、函数实现以及在图像分类中的应用。内容涵盖初始化参数、前向传播、损失函数、反向传播、参数更新等关键模块,并提供了测试用例。此外,还展示了2层和多层神经网络的模型结构及其实现细节,最后分析了模型在猫与非猫图像分类任务中的表现和错误案例。
本文详细介绍了吴恩达在Coursera上的深度学习课程《神经网络与深度学习》的编程作业,包括搭建深度神经网络的步骤、函数实现以及在图像分类中的应用。内容涵盖初始化参数、前向传播、损失函数、反向传播、参数更新等关键模块,并提供了测试用例。此外,还展示了2层和多层神经网络的模型结构及其实现细节,最后分析了模型在猫与非猫图像分类任务中的表现和错误案例。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章















 1323
1323

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








