习题一
5.
(1)
设事件A为从中任意抽取5片,至少是2片安慰剂
P ( A ) = C 5 2 C 5 3 + C 5 3 C 5 2 + C 5 4 C 5 1 + C 5 5 C 10 5 = 1 − P ( A ‾ ) = 1 − C 5 1 C 5 4 + C 5 5 C 10 5 = 226 252 = 113 126 \large {P(A)=\frac{C_{5}^{2}C_{5}^{3}+C_{5}^{3}C_{5}^{2}+C_{5}^{4}C_{5}^{1}+C_{5}^{5}}{C_{10}^{5}}=1-P(\overline A)}=1-\frac{C_{5}^{1}C_{5}^{4}+C_{5}^{5}}{C_{10}^{5}}=\frac{226}{252}=\frac{113}{126} P(A)=C105C52C53+C53C52+C54C51+C55=1−P(A)=1−C105C51C54+C55=252226=126113
t=choose(5,2)*choose(5,3)+choose(5,3)*choose(5,2)+choose(5,4)*choose(5,1)+choose(5,5)
s=choose(10,5)
p=t/s
p

(2)
设事件A为第一次取到安慰剂,事件B为第二次取到安慰剂,事件C为第三次取到安慰剂
P ( A B C ) = P ( C ∣ A B ) P ( B ∣ A ) P ( A ) = 1 2 ∗ 4 9 ∗ 3 8 = 1 12 \large{P(ABC)=P(C|AB)P(B|A)P(A)}=\frac{1}{2}*\frac{4}{9}*\frac{3}{8}=\frac{1}{12} P(ABC)=P(C∣AB)P(B∣A)P(A)=21∗94∗83=121

6.
(1)
设事件A为最小号码为5号
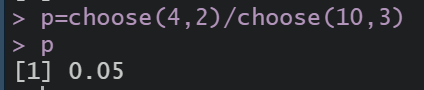
P ( A ) = C 5 2 C 10 3 = 1 12 \large{P(A)=\frac{C_{5}^{2}}{C_{10}^{3}}}=\frac{1}{12} P(A)=C103C52=121

(2)
设事件A为最大号码为5号
P ( A ) = C 4 2 C 10 3 = 1 20 \large{P(A)=\frac{C_{4}^{2}}{C_{10}^{3}}}=\frac{1}{20} P(A)=C103C42=201
7.
设事件A为顾客恰能按所订颜色如数得到订货
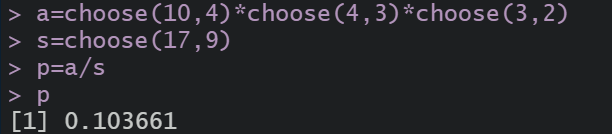
P ( A ) = C 10 4 C 4 3 C 3 2 C 17 9 = 252 2431 \large{P(A)=\frac{C_{10}^{4}C_{4}^{3}C_{3}^{2}}{C_{17}^{9}}=\frac{252}{2431}} P(A)=C179C104C43C32=2431252
8.
(1)
设事件A为恰有90件次品
P ( A ) = C 400 90 C 1100 110 C 1500 200 \large{P(A)=\frac{C_{400}^{90}C_{1100}^{110}}{C_{1500}^{200}}} P(A)=C1500200C40090C1100110
(太大了没算,见R代码及结果)

(2)
设事件A为至少有两件次品
P ( A ) = 1 − P ( A ‾ ) = 1 − C 400 1 C 1100 199 + C 1100 200 C 1500 200 \large{P(A)=1-P(\overline A)=1-\frac{C_{400}^{1}C_{1100}^{199}+C_{1100}^{200}}{C_{1500}^{200}}} P(A)=1−P(A)=1−C1500200C4001C1100199+C1100200

9.
设事件A为四只鞋子中至少有两只配成一双
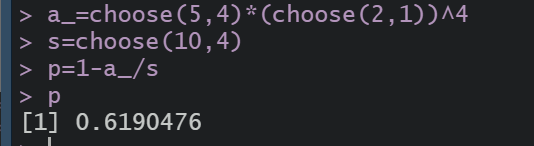
P ( A ) = 1 − P ( A ‾ ) = 1 − C 5 4 C 2 1 5 C 10 4 = 13 21 \large{P(A)=1-P(\overline A)=1-\frac{C_{5}^{4}{C_{2}^{1}}^5}{C_{10}^{4}}}=\frac{13}{21} P(A)=1−P(A)=1−C104C54C215=2113
10.
设事件A为其排列结果为ability
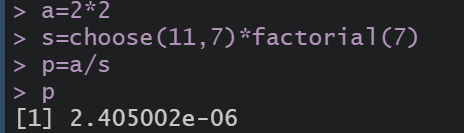
P ( A ) = C 1 1 C 2 1 C 2 1 C 1 1 C 1 1 C 1 1 C 1 1 A 11 7 = 1 415800 \large{P(A)=\frac{C_{1}^{1}C_{2}^{1}C_{2}^{1}C_{1}^{1}C_{1}^{1}C_{1}^{1}C_{1}^{1}}{A_{11}^{7}}}=\frac{1}{415800} P(A)=A117C11C21C21C11C11C11C11=4158001
11.
设事件A为杯子中球的最大个数为1
P ( A ) = C 4 3 3 4 \large{P(A)=\frac{C_{4}^{3}}{3^4}} P(A)=34C43
设事件B为杯子中球的最大个数为2
P ( B ) = C 4 1 C 3 2 3 4 \large{P(B)=\frac{C_{4}^{1}C_{3}^{2}}{3^4}} P(B)=34C41C32
设事件C为杯子中球的最大个数为3
P ( C ) = C 4 1 C 3 1 3 4 \large{P(C)=\frac{C_{4}^{1}C_{3}^{1}}{3^4}} P(C)=34C41C31

以上做法是错误的,再此感谢热心网友指出错误,下面说明下正解,以及错误原因
原题意思应该是每个杯子的都是本质不同的,例如:1 1 1 0 表示一二三号杯子各有一个球,但不等同于 0 1 1 1,同理得证及求球的个数的排列。
设事件A为杯子中球的最大个数为1
P ( A ) = A 4 3 4 3 \large{P(A)=\frac{A_{4}^{3}}{4^3}} P(A)=43A43
设事件B为杯子中球的最大个数为2
(三个球中选两个球捆绑一起,在对应投入杯中,下同理
P ( B ) = C 3 2 A 4 2 4 3 \large{P(B)=\frac{C_{3}^{2}A_{4}^{2}}{4^3}} P(B)=43C32A42
设事件C为杯子中球的最大个数为3
P ( C ) = C 3 3 A 4 1 4 3 \large{P(C)=\frac{C_{3}^{3}A_{4}^{1}}{4^3}} P(C)=43C33A41
R代码让我偷个懒 在此略过 (~ ̄▽ ̄)~
12.
设事件A为发生一个部件强度太弱
P ( A ) = C 10 1 C 47 3 . . . C 26 3 C 23 3 C 50 3 C 47 3 . . . C 26 3 C 23 3 = C 10 1 C 50 3 = 1 1960 \large{P(A)=\frac{C_{10}^{1}C_{47}^{3}...C_{26}^{3}C_{23}^{3}}{C_{50}^{3}C_{47}^{3}...C_{26}^{3}C_{23}^{3}}=\frac{C_{10}^{1}}{C_{50}^{3}}}=\frac{1}{1960} P(A)=C503C473...C263C233C101C473...C263C233=C503C101=19601
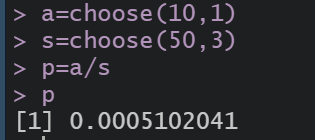
13.
(1)
设事件A为任选4名学生,一、二、三、四年级的学生各占一名
P ( A ) = C 5 1 C 2 1 C 3 1 C 2 1 C 12 5 = 4 33 \large{P(A)=\frac{C_{5}^{1}C_{2}^{1}C_{3}^{1}C_{2}^{1}}{C_{12}^{5}}=\frac{4}{33}} P(A)=C125C51C21C31C21=334

(2)
设事件A为任选5名学生,一、二、三、四年级的学生均包含在内
P ( A ) = C 5 2 C 2 1 C 3 1 C 2 1 + C 5 1 C 2 2 C 3 1 C 2 1 + C 5 1 C 2 1 C 3 2 C 2 1 + C 5 1 C 2 1 C 3 1 C 2 2 C 12 5 = 10 33 \large{P(A)=\frac{C_{5}^{2}C_{2}^{1}C_{3}^{1}C_{2}^{1}+C_{5}^{1}C_{2}^{2}C_{3}^{1}C_{2}^{1}+C_{5}^{1}C_{2}^{1}C_{3}^{2}C_{2}^{1}+C_{5}^{1}C_{2}^{1}C_{3}^{1}C_{2}^{2}}{C_{12}^{5}}}=\frac{10}{33} P(A)=C125C52C21C31C21+C51C22C31C21+C51C21C32C21+C51C21C31C22=3310

R

代码
详细解释在代码注释中
# 定义一个函数,该函数为所求的积分函数
# 因此在计算上述定积分和计算sqrt(2)同理
# 在此用例为sqrt(2)
f = function(x)
sqrt(2)
# 生成x
x = seq(1.5, 3.5, length=100)
y = rep(0, length(x))
j = 1
# 计算每个x对应的y值
for (i in x) {
y[j] = f(i)
j = j + 1
}
# 根据函数划出积分曲线
plot(x, y, type='o')
# 确定积分边界
abline(v = 2)
abline(v = 3)
# 简单设定随机点 (x,y)|2<=x<=3,0<=y<=100
# 即随机点的分布面积为100
s = 100
a = 0
cnt <- 1
# 有兴趣的朋友可以适当的多循环几次,这样结果更为精确,但是运行时间太长,并没有跑太久
while (cnt <= 100000) {
# 随机点 xx,yy
xx = 2 + runif(1)
yy = 100 * runif(1)
# 点在积分面积内则点为红色
if( f(xx) > yy ) {
a = a + 1
points(x = xx, y = yy, pch = 20, cex = 1, col = "red")
}
# 否则为绿色
else
points(x = xx, y = yy, pch = 20, cex = 1, col = "green")
cnt = cnt + 1
}
# 计算积分
print((a / 10000) * s)






















 1479
1479











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








