Dijkstra最短路径算法详解

简介

Dijkstra最短路径算法是非常经典的图搜索算法，而且具有一定难度，需要花时间好好理解。算法导论第24章对此有详细的分析，值得研究一番。而我自己也结合一个具体实例，实现了代码，确实只有在编码的过程中才能理解算法的细节，提高自己的算法能力。

实例分析

1.分步解析

Dijkstra最短路径算法也叫单源最短路径算法，意思就是只需要输入一个起点，求出该起点到图中其余点的最短路径即可。（而floyd则是求任意两点间的最短路径）
假如有如下有向图（无向图也可以，不能存在负值的边）：

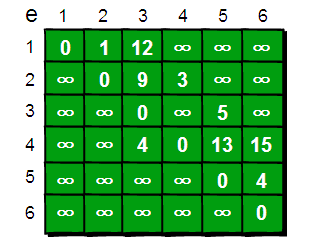
依旧使用二维数组存储这幅图的点和边：

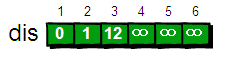
还需要一个distance数组，用于存储起点到其余终点的最短距离：

假设我们的起点即为1号顶点，由上图可知，此时它只有到点2，点3两条路。要找点1到剩余2,3,4,5,6号顶点的最短距离，那么当然只能先到点2，或点3，再到4,5,6号点。而应该通过走边（1–>2) 还是走边 （1–>3)再走到其他的点呢？相信正常人都会走最短的那条，也就是边(1–>2)。

也就是说，此时，我们要距离起点1，距离最近的点作为中转点，也就是2号点，将它加入到最短路径记录数组中。
既然选择了走2号点，那么从2号点出发，有两条路可走，先讨论通过（2–>3)这条边能否让1号顶点到3号顶点的路程变短。也就是说现在来比较distance[3]和distance[2]+e[2][3]的大小。其中distance[3]表示1号顶点到3号顶点的路程。distance[2]+e[2][3]中distance[2]表示1号顶点到2号顶点的路程，e[2][3]表示(2–>3)这条边。所以distance[2]+e[2][3]就表示从1号顶点先到2号顶点，再通过2->3这条边，到达3号顶点的路程。

我们发现原来的distance[3]=12，而distance[2]+e[2][3]=1+9=10，distance[3]>distance[2]+e[2][3]，因此dis[3]要更新为10。这个过程在算法导论中的专业术语叫做边的“松弛”。1号顶点到3号顶点的路程即distance[3]，通过2->3这条边松弛成功。这便是Dijkstra算法的主要思想：通过“边”来松弛1号顶点到其余各个顶点的路程。

同理，通过边（2–>4）（即e[2][4]），可以将distance[4]的值从∞松弛为4（distance[4]初始为∞，distance[2]+e[2][4]=1+3=4，distacne[4]>distance[2]+e[2][4]，因此dis[4]要更新为4）。

此时，对2号顶点所有的出边进行了