许多求最优解的问题可以用动态规划来解决。用动态规划解题,首先要把原问题分解为若干个子问题,这一点和前面的递归方法类似。区别在于,单纯的递归往往会导致子问题被重复计算,而用动态规划的方法,子问题的解一旦求出就会被保存,所以每个子问题只需求解一次。
子问题经常和原问题形式相似,有时甚至完全一样,只不过规模从原来的n变成了n-1,或从原来的n×m变成了n×(m-1) ……等等。找到子问题,就意味着找到了将整个问题逐渐分解的办法,因为子问题可以用相同的思路分解成子子问题,一直分解下去,直到最底层规模最小的的子问题可以一目了然地看出解(象上面数字三角形的递推公式中,r=N时,解就是一目了然的)。每一层子问题的解决,会导致上一层子问题的解决,逐层向上,就会导致最终整个问题的解决。如果从最底层的子问题开始,自底向上地推导出一个个子问题的解,那么编程的时候就不需要写递归函数。
在用动态规划解题时,我们往往将和子问题相关的各个变量的一组取值,称之为一个“状态”。一个“状态”对应于一个或多个子问题,所谓某个“状态”下的“值”,就是这个“状态”所对应的子问题的解。
具体到数字三角形的例子,子问题就是“从位于(r,j)数字开始,到底边路径的最大和”。这个子问题和两个变量r和j相关,那么一个“状态”,就是r, j的一组取值,即每个数字的位置就是一个“状态”。该“状态”所对应的“值”,就是从该位置的数字开始,到底边的最佳路径上的数字之和。
定义出什么是“状态”,以及在该 “状态”下的“值”后,就要找出不同的状态之间如何迁移―――即如何从一个或多个“值”已知的 “状态”,求出另一个“状态”的“值”。状态的迁移可以用递推公式表示,此递推公式也可被称作“状态转移方程”。
子问题经常和原问题形式相似,有时甚至完全一样,只不过规模从原来的n变成了n-1,或从原来的n×m变成了n×(m-1) ……等等。找到子问题,就意味着找到了将整个问题逐渐分解的办法,因为子问题可以用相同的思路分解成子子问题,一直分解下去,直到最底层规模最小的的子问题可以一目了然地看出解(象上面数字三角形的递推公式中,r=N时,解就是一目了然的)。每一层子问题的解决,会导致上一层子问题的解决,逐层向上,就会导致最终整个问题的解决。如果从最底层的子问题开始,自底向上地推导出一个个子问题的解,那么编程的时候就不需要写递归函数。
在用动态规划解题时,我们往往将和子问题相关的各个变量的一组取值,称之为一个“状态”。一个“状态”对应于一个或多个子问题,所谓某个“状态”下的“值”,就是这个“状态”所对应的子问题的解。
具体到数字三角形的例子,子问题就是“从位于(r,j)数字开始,到底边路径的最大和”。这个子问题和两个变量r和j相关,那么一个“状态”,就是r, j的一组取值,即每个数字的位置就是一个“状态”。该“状态”所对应的“值”,就是从该位置的数字开始,到底边的最佳路径上的数字之和。
定义出什么是“状态”,以及在该 “状态”下的“值”后,就要找出不同的状态之间如何迁移―――即如何从一个或多个“值”已知的 “状态”,求出另一个“状态”的“值”。状态的迁移可以用递推公式表示,此递推公式也可被称作“状态转移方程”。
如下的递推式就说明了状态转移的方式:
上面的递推式表明了如果知道了状态(r+1,j)和状态(r+1,j+1)对应的值,该如何求出状态(r,j)对应的值,即两个子问题的解决,如何导致一个更高层的子问题的解决。
所有“状态”的集合,构成问题的“状态空间”。“状态空间”的大小,与用动态规划解决问题的时间复杂度直接相关。在数字三角形的例子里,一共有N×(N+1)/2个数字,所以这个问题的状态空间里一共就有N×(N+1)/2个状态。在该问题里每个“状态”只需要经过一次,且在每个状态上作计算所花的时间都是和N无关的常数。
用动态规划解题,经常碰到的情况是,K个整型变量能构成一个状态(如数字三角形中的行号和列号这两个变量构成“状态”)。如果这K个整型变量的取值范围分别是N1, N2, ……Nk,那么,我们就可以用一个K维的数组array[N1] [N2]……[Nk]来存储各个状态的“值”。这个“值”未必就是一个整数或浮点数,可能是需要一个结构才能表示的,那么array就可以是一个结构数组。一个“状态”下的“值”通常会是一个或多个子问题的解。
用动态规划解题,如何寻找“子问题”,定义“状态”,“状态转移方程”是什么样的,并没有一定之规,需要具体问题具体分析,题目做多了就会有感觉。甚至,对于同一个问题,分解成子问题的办法可能不止一种,因而“状态”也可以有不同的定义方法。不同的“状态”定义方法可能会导致时间、空间效率上的区别。








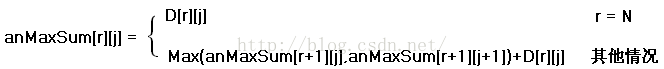














 675
675

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








