方格填数

方格填数

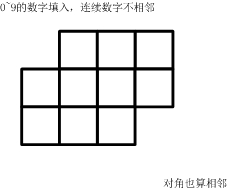
如图，如下的10个格子，填入0~9的数字。要求：连续的两个数字不能相邻。
（左右、上下、对角都算相邻）一共有多少种可能的填数方案？
请填写表示方案数目的整数。

思路：这题方法很简单，暴力求解，依次向每个格子填数与已经填入的进行比较是否连续，即：是否两者之差的绝对值为1。比赛的时候一直在纠结，题干没有说明0~9的数字可以重复使用还是只能用一次，比赛时最后我按照可以重复使用提交的，不知道是不是正确。

思路：每一个格子可能数字都是0到9，所以暴力解决就用多重循环来解决，控制条件是每个数字之间是不相等的而且相邻之间的数字是不能连续的。

数字之间连续的判断条件是：相减绝对值为1。

#include<bits/stdc++.h>
using namespace std;
int main(){
	int a,b,c,d,e,f,g,h,i,j;
	int cnt=0;
	for(a=0;a<=9;a++){
		for(b=0;b<=9;b++){
			if(a==b||abs(b-a)==1)
			  continue;
			for(c=0;c<=9;c++){
				if(a==c||b==c||abs(c-b)==1)
				 continue;
				for(d=0;d<=9;d++){
					if(a==d||b==d||c==d||abs(d-a)==1)
					  continue;
					for(e=0;e<=9;e++){
						if(a==e||b==e||c==e||d==e||abs(e-a)==1||abs(e-d)==1||abs(e-b)==1)
						 continue;
						for(f=0;f<=9;f++){
							if(a==f||b==f||c==f||d==f||e==f||abs(f-e)==1||abs(f-b)==1||abs(f-c)==1||abs(f-a)==1)
							  continue;
							for(g=0;g<=9;g++){
								if(a==g||b==g||c==g||d==g||e==g||f==g||abs(g-c)==1||abs(g-f)==1||abs(g-b)==1)
								 continue;
								for(h=0;h<=9;h++){
									if(a==h||b==h||c==h||d==h||e==h||f==h||g==h||abs(h-d)==1||abs(h-e)==1)
									 continue;
									for(i=0;i<=9;i++){
										if(a==i||b==i||c==i||d==i||e==i||f==i||g==i||h==i||abs(i-h)==1||abs(i-e)==1||abs(i-f)==1||abs(i-d)==1)
											 continue;
										for(j=0;j<=9;j++){
										  if(a==j||b==j||c==j||d==j||e==j||f==j||g==j||h==j||i==j||abs(j-i)==1||abs(j-f)==1||abs(j-e)==1||abs(j-g)==1)
										    continue;
										  cnt++;	
										}
									}
								}
							}
						}
					}
				}
			}
		}
	}
	cout<<cnt<<endl;
}