二叉树的遍历

一、二叉树的遍历方式

提到二叉树的遍历，最常见的有以下几种方式：

• 前序遍历：根->左->右
• 中序遍历：左->根->右
• 后序遍历：左->右->根
• 层序遍历：从左到右，从上到下遍历根节点

在开始讲解前，我们先定义好树节点的结构

public class TreeNode
{
	public int Val;
	public TreeNode Left;
	public TreeNode Right;

	public TreeNode(int x)
	{
		Val = x;
	}
}

二、递归实现

对于二叉树的前、中、后序遍历，采用递归方式实现将异常简单。我们首先考虑如何如何递归地遍历一棵二叉树，而不考虑遍历的顺序。很容易想到如下的实现方式

private void TraverseTree(TreeNode? root)
{
	if(root == null)
		return;
	TraverseTree(root.Left);
	TraverseTree(root.Right);
}

也就是说，对于任何一棵子树，我们先遍历到它的根节点，然后再去分别遍历它的左子树和右子树。

2.1 前序遍历

那么假如我们每遍历到一个根节点就将根节点输出，则输出逻辑就是：先输出当前树的根节点，再去左子树上找左子树的根节点并输出…直到找到叶子节点，然后停止递归并开始回溯。在回溯途中，如果找到了右子树，那就输出右子树的根节点，然后继续去左子树寻找。这实际上就是前序遍历（根->左->右）的遍历方式。

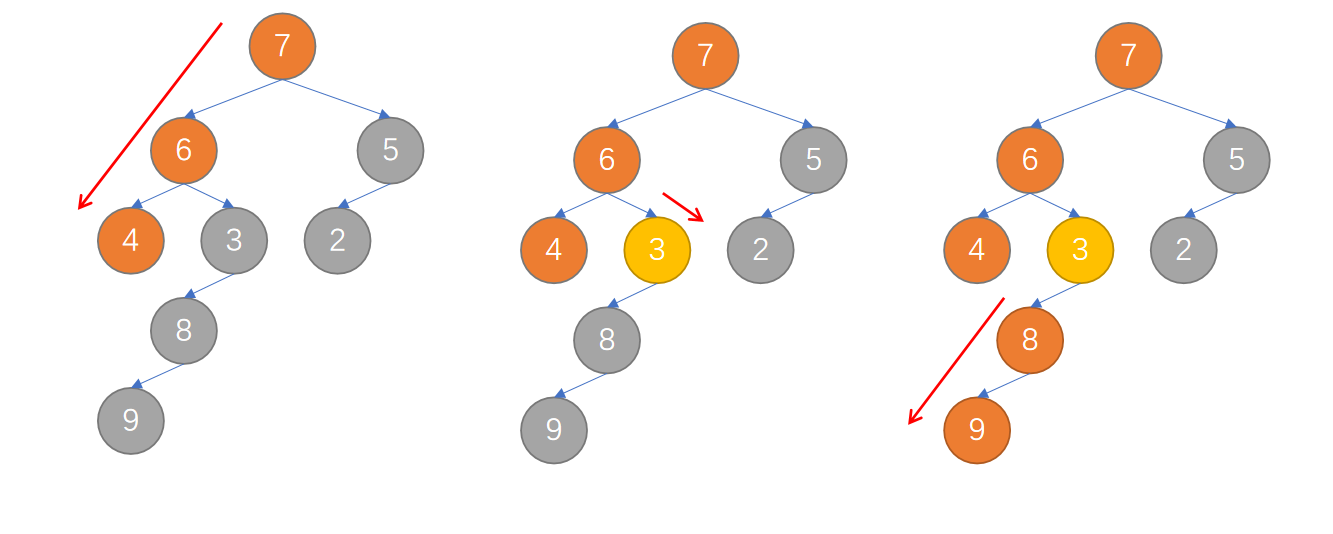
代码如下

private void TraverseTree(TreeNode? root)  
{  
    if(root == null)  
        return;  
    Console.Write(root.Val+" ");  
    TraverseTree(root.Left);  
    TraverseTree(root.Right);  
}

2.2 中序遍历

如果在遍历完左子树之后再输出根节点，那么输出逻辑就会变为：只要当前节点存在左子树，就往左子树遍历。直到遍历到的节点没有左子树，则输出根节点。然后再去右子树上，重复上述过程。遍历完右子树后，开始回溯。这就是中序遍历（左->根->右）的遍历方式。

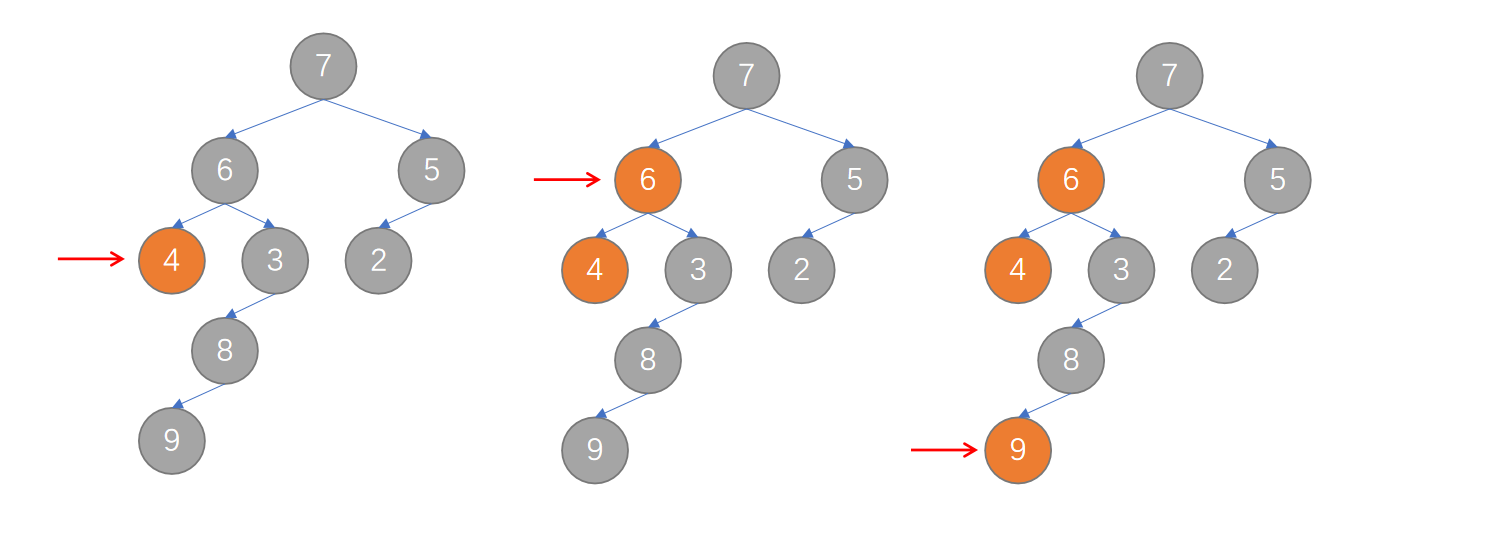
代码如下

private void TraverseTree(TreeNode? root)
{
	if(root == null)
		return;
	TraverseTree(root.Left);
	Console.Write(root.Val+" ");
	TraverseTree(root.Right);
}

2.3 后续遍历

如果在遍历完右子树之后再输出根节点，则输出逻辑会变为：只要当前节点存在左子树，就继续往左子树遍历。如果当前节点没有左子树，但有右子树，则往右子树遍历。直到当前节点既没有左子树也没有右子树，就开始回溯，输出根节点。这就是后序遍历（左->右->根）的遍历方式。

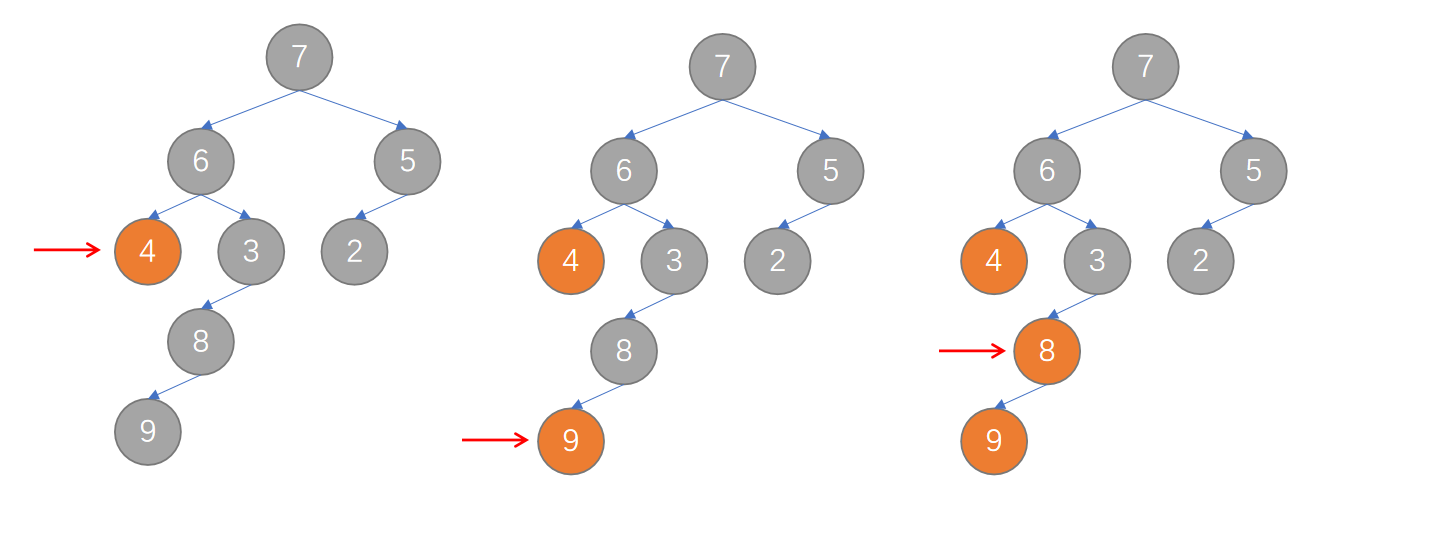
2.4 层序遍历

层序遍历采用递归方式实现就有点复杂了，因为在不借助外部存储结构的情况下，我们无法记录正确的输出顺序。所以要么用集合记录每一层遍历到的节点，要么先得出树的高度，再一层一层的进行递归。

首先是使用集合记录的方式

private List<List<int>> res = new();
private void LevelOrder1(TreeNode? root, int i = 0)
{
	if(root == null)
		return;
	if(res.Count < i+1)
		res.Add(new List<int>());
	res[i].Add(root.Val);
	LevelOrder1(root.Left,i+1);
	LevelOrder1(root.Right,i+1);
}

其次是先求出高度，然后再层层递归的方式

private void LevelOrder2En(TreeNode? root)
{
	int height = GetTreeHeight(root);
	for (int i = 0; i < height; i++)
	{
		LevelOrder2(root, i);
	}
}

private void LevelOrder2(TreeNode? root, int i)
{
	if(root == null)
		return;
	if(i == 0)
		Console.Write(root.Val+" ");
	LevelOrder2(root.Left,i-1);
	LevelOrder2(root.Right,i-1);
}
// 获取树的高度
private int GetTreeHeight(TreeNode? root)
{
	if (root == null)
		return 0;
	return Math.Max(GetTreeHeight(root.Left), GetTreeHeight(root.Right))+1;
}

三、非递归实现

通过递归实现二叉树的遍历，实际上是系统在维护一个栈。而非递归实现实际上就是我们通过手工方式维护一个栈。

3.1 前序遍历

前序遍历的非递归实现流程是：
① 先将根节点压栈
② 弹出栈顶元素并输出，然后先将右孩子压栈，再将左孩子压栈（这样在弹出时才是先左后右）
③ 重复②步骤直到栈弹空

代码如下

private void Preorder(TreeNode? root)
{
	if(root == null)
		return;
	var stack = new Stack<TreeNode>();
	stack.Push(root);
	while (stack.Count > 0)
	{
		var node = stack.Pop();
		Console.Write(node.Val+" ");
		if(node.Right != null)
			stack.Push(node.Right);
		if(node.Left != null)
			stack.Push(node.Left);
	}
}

3.2 中序遍历

中序遍历的非递归实现流程是：
① 从根节点开始遍历左孩子，并依次入栈，直到遍历到空
② 弹出栈顶元素并输出，如果有右孩子，则重复①，否则重复②
③ 栈弹空时跳出

代码如下

private void Inorder(TreeNode? root)
{
	if(root == null)
		return;
	var stack = new Stack<TreeNode>();
	var curNode = root;
	while (stack.Count > 0 || curNode != null)
	{
		// 不为空则入栈,继续寻找左孩子
		if (curNode != null)
		{
			stack.Push(curNode);
			curNode = curNode.Left;
		}
		// 为空则弹出栈顶元素,对右孩子进行上述操作
		else
		{
			curNode = stack.Pop();
			Console.Write(curNode.Val+" ");
			curNode = curNode.Right;
		}
	}
}

3.3 后序遍历

后序遍历的非递归实现流程是：
① 先将根节点入栈A
② 弹出栈A元素，将该元素压入栈B，其左孩子、右孩子先后入栈A
③ 重复②直到栈A为空，依次输出栈B

代码如下

private void Postorder(TreeNode? root)
{
	if(root == null)
		return;
	var stackA = new Stack<TreeNode>();
	var stackB = new Stack<TreeNode>();
	stackA.Push(root);
	while (stackA.Count > 0)
	{
		var node = stackA.Pop();
		stackB.Push(node);
		if(node.Left != null)
			stackA.Push(node.Left);
		if(node.Right != null)
			stackA.Push(node.Right);
	}

	while (stackB.Count > 0)
	{
		Console.Write(stackB.Pop().Val+" ");
	}
}

3.4 层序遍历

层序遍历的非递归实现就比较简单了，只需要通过一个队列就可以实现

private void LevelOrder(TreeNode? root)
{
	if(root == null)
		return;
	var queue = new Queue<TreeNode>();
	queue.Enqueue(root);
	while (queue.Count > 0)
	{
		var node = queue.Dequeue();
		Console.Write(node.Val+" ");
		if(node.Left != null)
			queue.Enqueue(node.Left);
		if(node.Right != null)
			queue.Enqueue(node.Right);
	}
}