在Logistic回归中,我们接触到了分类任务,今天我们将要介绍的是决策树,它是一种用于分类与回归的算法,这里主要讨论用于分类的决策树。
决策树初探
从名字中就不难猜出决策树模型是呈树形结构,在分类问题中,基于特征对实例进行分类,我们可以想象有一系列的if-else规则集合,通过判断特征是否符合这些规则来对实例进行分类。
决策树结构
决策树是一种对实例进行分类的树形结构,它由结点和有向边组成。而结点又分为内部结点和叶子结点,内部结点用来对特征或属性进行判断,叶子结点表示对应的类。
从上面的图可以看出,在每个内部结点内都对属性进行判断然后将样本划分成两部分,因此,应该如何选择对哪个属性进行判断才能更快地得到一棵树呢。
我们希望决策树的内部结点包含的样本尽可能属于同一类,也就是结点的“纯度”越来越高。
信息增益
我们用信息熵(information entropy)来度量样本集合的纯度,对于样本集D中第k类,其所占比例为pk(k=1,2,···,y),那么D的信息熵定义为:
E
n
t
(
D
)
=
−
∑
k
=
1
y
p
k
l
o
g
2
p
k
Ent(D) = - \sum_{k=1}^yp_klog_2p_k
Ent(D)=−k=1∑ypklog2pk
Ent(D)的值越小,那么D的纯度越高。
样本集D在属性a上的信息增益(information gain)为:
G
a
i
n
(
D
,
a
)
=
E
n
t
(
D
)
−
∑
v
=
1
V
∣
D
v
∣
∣
D
∣
E
n
t
(
D
v
)
Gain(D, a)=Ent(D) - \sum_{v=1}^V \frac{|D^v|}{|D|} Ent(D^v)
Gain(D,a)=Ent(D)−v=1∑V∣D∣∣Dv∣Ent(Dv)
其中V表示a可能的取值,
D
v
D^v
Dv表示属性a上取值为V的样本数。
信息增益越大,说明使用属性a进行划分能获得的纯度提升越大。但是这么做有个缺陷,对于取值比较多的属性,比如ID,日期等,使用这种属性进行划分产生的纯度会很大,但很明显这种属性不适合用来作为划分。事实上,信息增益对取值数目较多的属性会有所偏好,因此,我们不直接使用信息增益,而使用增益率。
增益率
信息增益率(gain ratio)定义为:
G
a
i
n
_
r
a
t
i
o
(
D
,
a
)
=
G
a
i
n
(
D
,
a
)
I
V
(
a
)
Gain\_ratio(D, a) = \frac{Gain(D, a)}{IV(a)}
Gain_ratio(D,a)=IV(a)Gain(D,a)
I V ( a ) = − ∑ v = 1 V ∣ D v ∣ ∣ D ∣ l o g 2 ∣ D v ∣ ∣ D ∣ IV(a) = -\sum_{v=1}^V\frac{|D^v|}{|D|}log_2 \frac{|D^v|}{|D|} IV(a)=−v=1∑V∣D∣∣Dv∣log2∣D∣∣Dv∣
IV(a)成为属性a的固有值(intrinsic value),属性a的可能取值越多,那么IV(a)越大。
然而,增益率对取值比较少的属性有所偏好,因此在C4.5算法中并没有直接选择增益率最大的属性进行划分,而是采用启发式的方式,先找出信息增益高于平均水平的属性,再选择增益率最高的。
基尼指数
在CART算法中,使用基尼指数(Gini index)来选择划分属性,用基尼值来度量数据集D的纯度。
G
i
n
i
(
D
)
=
∑
k
=
1
y
∑
k
′
̸
=
k
p
k
p
k
′
=
1
−
∑
k
=
1
y
p
k
2
Gini(D) = \sum_{k=1}^y \sum_{k' \not=k} p_kp_{k'} = 1 - \sum_{k=1}^yp_k^2
Gini(D)=k=1∑yk′̸=k∑pkpk′=1−k=1∑ypk2
Gini(D)反应了从数据集中随机抽取两个样本,它们属于不同类的概率,因此Gini(D)越小,那么数据集D的纯度越高,那么属性a的基尼指数为:
G
i
n
i
_
i
n
d
e
x
(
D
,
a
)
=
∑
v
=
1
V
∣
D
v
∣
∣
D
∣
G
i
n
i
(
d
v
)
Gini\_index(D, a) = \sum_{v=1}^V \frac{|D^v|}{|D|}Gini(d^v)
Gini_index(D,a)=v=1∑V∣D∣∣Dv∣Gini(dv)
因此,选择基尼指数最小的那个属性进行划分。
树剪枝
在生成决策树时,往往会产生树对训练数据分类很准确,但对未知数据不那么准确,出现了过拟合现象,这是因为在训练过程中过多的考虑如何提高对训练数据的正确分类,而将训练数据自身的一些特点当做所有数据的共性而学习进去,因此产生了较为复杂的树,因此使用剪枝的方式来简化树结构。
剪枝分为预剪枝和后剪枝。
预剪枝是在决策树生成过程中,在每个结点划分前先进行估计,如果不能带来泛化性能提升,那么不进行划分。但是,在处理某些结点时,虽然不能立刻带来泛化提升,但是在它的基础上的后续划分可能会提高泛化性能,因此预剪枝这种贪心性质会带来欠拟合风险。
而后剪枝是先训练好一棵树,再自底向上对内部结点进行考察,如果将它替换成叶结点能带来泛化性能提升,那么将它替换成叶结点。后剪枝的欠拟合风险小,但是它需要在生成一棵完整的树之后再进行剪枝,因此时间开销和最终树都比预剪枝大。
实践一下
初学者看到这么多的公式是不是吓了一跳,不用担心,Scikit-learn中已经帮我们实现好了,我们现在拿它来用一用,这里使用到的数据就是家喻户晓的鸢尾花卉数据集,它包含四个特征花萼长度,花萼宽度,花瓣长度,花瓣宽度,三个种类,Setosa,Versicolour,Virginica,一共有150条数据。
为方便可视化,我们先将特征两两组合,训练一个决策树模型,然后看看它的分类结果:
for pairidx, pair in enumerate([[0, 1], [0, 2], [0, 3],
[1, 2], [1, 3], [2, 3]]):
# We only take the two corresponding features
X = iris.data[:, pair]
y = iris.target
# Train
clf = DecisionTreeClassifier().fit(X, y)
# Plot the decision boundary
plt.subplot(2, 3, pairidx + 1)
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, plot_step),
np.arange(y_min, y_max, plot_step))
plt.tight_layout(h_pad=0.5, w_pad=0.5, pad=2.5)
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
cs = plt.contourf(xx, yy, Z, cmap=plt.cm.RdYlBu)
plt.xlabel(iris.feature_names[pair[0]])
plt.ylabel(iris.feature_names[pair[1]])
# Plot the training points
for i, color in zip(range(n_classes), plot_colors):
idx = np.where(y == i)
plt.scatter(X[idx, 0], X[idx, 1], c=color, label=iris.target_names[i],
cmap=plt.cm.RdYlBu, edgecolor='black', s=15)

接下来使用所有特征训练决策树并画出树结构:
clf = DecisionTreeClassifier().fit(iris.data, iris.target)
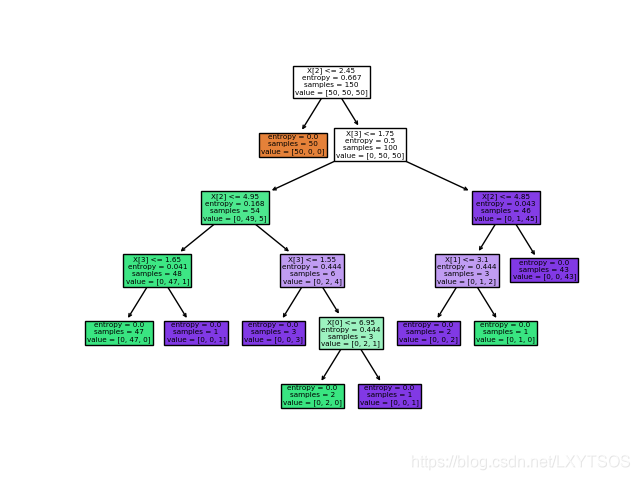
plot_tree(clf, filled=True)
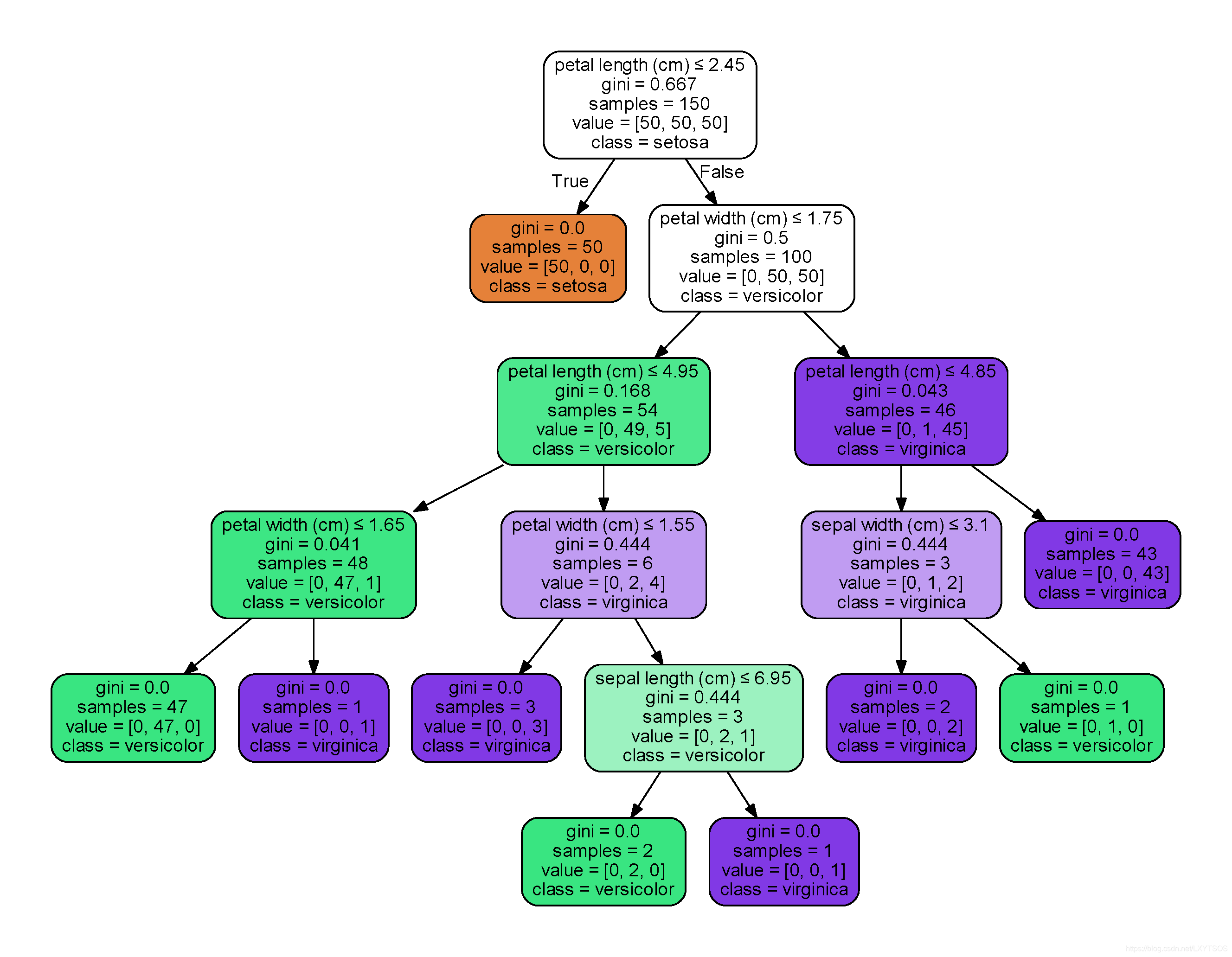
仔细看会发现,上面的树结构中,属性是用下标表示,类别也是用数组表示,不方便阅读,那么下面用graphviz将树结构更友好地显示出来:
dot_data = export_graphviz(clf, out_file=None, feature_names=iris.feature_names, class_names=iris.target_names,
filled=True, rounded=True, special_characters=True)
graph = graphviz.Source(dot_data)
graph.render('iris')
扫码关注微信公众号:机器工匠,回复关键字“决策树”获取实现代码。

























 1万+
1万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








