logistic回归算法原理及python实现

1 logistic回归与sigmoid函数

考虑如下线性函数：

$$\begin{equation} y=\pmb{w}^\rm{T}\pmb{x}+b \tag{1} \end{equation}$$
输出 $y$为连续的实值，如何让输出成为二值来完成二分类任务？即 $y \in \{0,1\}$,最理想的是单位阶跃函数即：
$$\begin{equation} y= \left\{ \begin{array}{lll} 0,\qquad z<0& \\ 0.5,\quad z=0 & \\ 1,\qquad z>0&\\ \end{array} \tag{2} \right. \end{equation}$$
但是，单位阶跃函数不连续，不利于求解权值，构建模型。于是sigmoid函数（对数几率函数，logistic function）出现了，他单调可微，并且形似阶跃函数，其公式描述如下所示:
$$\begin{equation} y=\frac{1}{1+e^{-(\pmb{w}^\rm{T}\pmb{x}+b )}}\tag{3} \end{equation}$$
sigmoid曲线如下图所示：

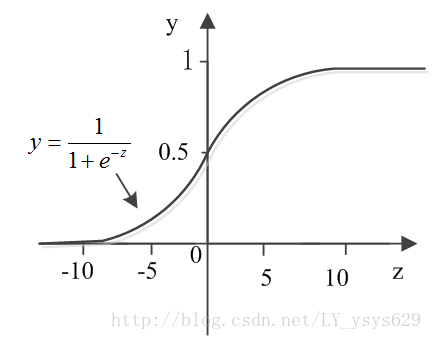
令$y$表示当输入为$x$时，输出为正例的概率（可能性），即$y=P(Y=1|X=x)$,$1-y$表示当输入为$x$时，输出为反例的概率（可能性），即$1-y=P(Y=0|X=x)$，两者的比值$\frac{y}{1-y}$称为几率（odds），对其取对数即达到对数几率，所以logistic回归又称为对数几率回归。因此根据（2）可得对数几率回归（logistic回归）公式如下所示：

$$\begin{equation} \log \frac{y}{1-y}=\pmb{w}^\rm{T}\pmb{x}+b \tag{4} \end{equation}$$

2 二项逻辑斯蒂回归模型与参数估计

由式（3）可得二项逻辑斯蒂回归模型如下所示：