人体骨骼图像增强【分析+Python代码】

一、设计思路

由于对于人体骨骼灰度图的动态范围计较窄，并且噪声比较大，单靠一种滤波或锐化算子无法较好的实现图像的细节增强。故通过设计一种混合的图像增强的方式如下图所示。

根据上图可知，首先通过对原图像img做拉普拉斯算子运算增强突出图像细节，接着将图laplacian与img图像叠加得到图img_laplacian。又因为二阶求导的拉普拉斯算子也会使得图像的噪声增强，而一阶求导的Sobel算子对噪声和小细节的响应较弱。所以通过对原图像img做X和Y两个维度的Sobel算子运算并相加得到图Sobel。进一步可以对图Sobel进行双边滤波，平滑噪声并保留细节，得到图Blur。然后将平滑后的图Blur和图img_laplacian相乘，乘积可以保留灰度变化强烈区域的细节，同时降低灰度变化相对平坦区域的噪声。最后将结果叠加在原图img，并做灰度图幂变化扩展灰度图范围即可得到最终混合增强的锐化图像。

二、实验结果分析

对图像做拉普拉斯运算（需要注意后面运算得到的图像需要将其灰度值映射到0-255范围内）
将其叠加在原图像上，可以略微观察出骨骼细节的增加
对原图像做Sobel运算，增强了细小的细节，但是噪声也被增加了。
对Sobel运算得到的图像进行双边滤波，可以平滑噪声保留边界；在书中利用的为均值滤波，我认为此处由于灰度范围比较窄，实际我也使用了均值滤波进行对比，实际差距不大。但是我觉得运用双边滤波会更好一些。
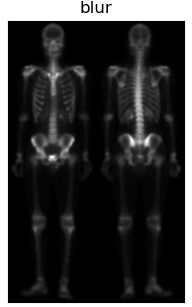将滤波后的图sobel与图img_laplacian进行相乘，保留变化强烈的细节，平滑噪声
将相乘得到的图masking叠加到原图上
由于图像灰度范围窄，整体偏暗，在此使用灰度幂变换扩展灰度范围，使得更符合人眼观察。

根据幂律（伽马）变换基本形式：
$$s=c{r}^{\gamma }$$
在此选择$\gamma =0.5,c=1$,最终得到的混合增强图像如下，可以看出人体的外形轮廓清晰，手腕，手掌等骨骼细节由人眼也可观察到。

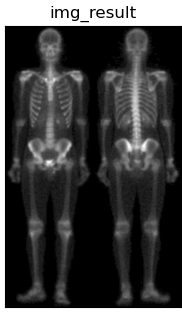最终将各结果进行对比显示

三、补充讨论

在一篇论文《基于Matlab工具的医学图像混合空间增强算法研究》中的处理方法为：首先进行直方图均衡化、规定化提升对比度,然后用Laplace变换突出图像中的小细节，接着用canny算子进行边缘检测,最后将Laplace变换后的图像与边缘检测后的图像相乘,再加上提升对比度后的图像,得到混合空间增强图像。

1. 对于使用直方图均衡化的方法，由于待处理图像较暗，处理后会出现许多杂点和噪声点，效果并不好。

2. 对于使用canny算子进行边缘细节检测，由于图像灰度范围窄，噪声大，实际通过调节上下阈值无法较好的获取边缘细节。

故综上实验中设计的混合图像增强方法效果更好。

四、Python代码

import numpy as np
import cv2
from matplotlib import pyplot as plt

#将灰度值映射到[0,255]的区间
def convert_gray255(image):
    image_r = 255*(image - image.min())/(image.max() - image.min())
    return(image_r)

################图像处理################
#plt.figure(figsize=(40,40))   #创建图片显示窗口大小
img = cv2.imread('img.bmp', 0)
laplacian = convert_gray255(cv2.Laplacian(img, cv2.CV_64F))
img_laplacian = convert_gray255(img + laplacian)
# 参数1,0 为只在x 方向求一阶导数，最大可以求2 阶导数。
sobelx = cv2.Sobel(img, cv2.CV_64F, 1, 0, ksize=3)
# 参数0,1 为只在y 方向求一阶导数，最大可以求2 阶导数。
sobely = cv2.Sobel(img, cv2.CV_64F, 0, 1, ksize=3)
sobel=np.clip(np.abs(sobelx) + np.abs(sobely),0,255)
blur = cv2.bilateralFilter(img,9,75,75)
masking = convert_gray255(blur * img_laplacian)
img_masking =convert_gray255(img + masking)
img_result = 1*((img_masking)**0.5)

################图像绘制################
plt.subplot(2, 4, 1), plt.imshow(img, cmap='gray')
plt.title('Original'), plt.xticks([]), plt.yticks([])
plt.subplot(2, 4, 2), plt.imshow(laplacian, cmap='gray')
plt.title('Laplacian'), plt.xticks([]), plt.yticks([])
plt.subplot(2, 4, 3), plt.imshow(img_laplacian, cmap='gray')
plt.title('img_laplacian'), plt.xticks([]), plt.yticks([])
plt.subplot(2, 4, 4), plt.imshow(sobel, cmap='gray')
plt.title('sobel'), plt.xticks([]), plt.yticks([])
plt.subplot(2, 4, 5), plt.imshow(blur, cmap='gray')
plt.title('blur'), plt.xticks([]), plt.yticks([])
plt.subplot(2, 4, 6), plt.imshow(masking, cmap='gray')
plt.title('masking'), plt.xticks([]), plt.yticks([])
plt.subplot(2, 4, 7), plt.imshow(img_masking, cmap='gray')
plt.title('img_masking'), plt.xticks([]), plt.yticks([])
plt.subplot(2, 4, 8), plt.imshow(img_result, cmap='gray')
plt.title('img_result'), plt.xticks([]), plt.yticks([])

plt.show()