各位小伙伴们好,我是努力学习AI算法的超级驼鹿,今天跟大家分享线性回归的原理和推导过程。
相信大家对下面两个图已经很熟悉了,今天我们就讲讲计算机是如何通过“学习”左边的蓝色点的数据拟合出右边这样一条 y = x 的直线的。


---------------------------------------------------------------------------------------------------------------------------------
首先,我们要知道我们给计算机的数据是什么样子的:
当然是左边一个个蓝色的点了
----也就是对应点的横纵坐标x与y的值,假设左边一共有n个点,那么我们就会有(x1,x2,x3,......,xn)个横坐标和对应的(y1,y2,y3,......,yn)个纵坐标,其中(y1,y2,y3......,yn)是真实的值,它们是我们的计算机要学习的“知识”,每个y都只受其对应的x值的影响,我们将y称为目标值,x称为特征。
---------------------------------------------------------------------------------------------------------------------------------
那么好了,请问各位小伙伴,我们的计算机现在要做的工作是什么呢?
当然是要根据所有的点拟合出一条“最符合”这些点分布规律的直线了,也就是说要找出y=wx+b中的w和b两个未知数,这样,我们的特征x经过w和b的运算,就能够得出目标值y了。
(因为是线性回归所以默认需要拟合的点的规律是一条直线的形式,也就是y=wx+b,后面会有不同的回归算法来解决需要拟合的点不是线性的问题)

---------------------------------------------------------------------------------------------------------------------------------
问题来了:我们应该如何评价这个“最符合”呢?
换句话说,你凭什么说 y = x 比 y = x + 1 更贴近于图片中数据点分布的情况呢?
 (红线:y=x 黑线:y=x+1)
(红线:y=x 黑线:y=x+1)
凭我们的感觉吗?哈哈哈当然可以且正确!诚然,我们人类的大脑是很聪明的,但计算机可没有感觉一说。小伙伴们可以想想,有什么办法来描述一条直线与对应点的符合程度呢?
为了描述这条线符合的情况,我们选择了让所有真实点到这条预测直线上的点的差值最小,这样我们就可以认为这条直线是“最符合”的。就好帮派内斗,无论哪方胜出,另一方都要遭受重大的损失,使帮派总体实力大减,但如果双方能和解,达成共识,虽然各有损失,但不至于让整个帮派没落下去。所以我们的任务就是找到这个公平的和事佬。
让我们显得专业一点的表达就是:
令:是根据我们“最合适”直线的方程预测出来的目标值,y是真实值,x是特征
则:对于相同的特征x,其对应的预测值与真实y差值的绝对值称为这个特征x的误差值,用
来表示
即: = |
- y |
这就是单个特征点x的误差值了
---------------------------------------------------------------------------------------------------------------------------------
接下来我们需要做一个重要的假设:假设我们所有误差的分布服从于正态分布(高斯分布),并且所有误差的形成是独立的(就是概率事件上的独立)。
由于误差的出现是随机的,而随机数据的数量一旦变得很大很多,那么我们就可以先默认为,它们是服从正态分布的。这是高斯这个天才数学家,在对自然界各种各样的数据数值做出分析评估之后得出来的分布,大自然的很多很多数值特征都会尊从正态分布。
直观一点的来说,人的身高,当统计数量足够多的时候,遵从的分布就是正态分布,特别高的人,像姚明,就很少,特别矮的人,像夏雨轩,也很少,大部分人都是“中不溜”的身高,就像你我一样。年龄、学习成绩等一系列看起来毫无关系的数据,都会遵从正态分布,是不是很神奇?
 (正态分布图像)
(正态分布图像)
---------------------------------------------------------------------------------------------------------------------------------
回到正轨,我们的误差独立且服从于正态分布,那我们就可以用最大似然法来计算了!
等等,什么是最大似然?让我来给你简单解释一下吧:最大似然就是根据已观测到的现象倒推最有可能导致这种现象发生的参数的方法。
呃,有点复杂。那我们来举个例子吧:一个盒子里放着黑球和白球,你不知道里面黑球占了多少比例,白球占了多少比例,现在让你每次从箱子里摸出一个球,看看他的颜色并记录,再将其放回至盒中,你摸了100次,其中70次摸出来的是黑球,30次摸出来的是白球,请问箱子里黑白球的占比最有可能是多少?
----当然是黑球占了70%,白球占了30%!
没错,你已经完成了一次最大似然估计了!
对于这个问题来说,每个误差发生的概率可以用正态分布的概率密度函数
 计算,其中
计算,其中为正态分布的期望,
是正态分布的方差,由于我们估计要的是总误差而不是单个误差值,我们总有办法(例如改变其函数的截距)使其期望
变为0(目的仅仅是为了方便计算且不会影响最终结果)
所以最终我们单个误差出现的概率为:![]()
又因为我们每个误差的出现是独立的,所以出现我们这一组误差的总概率P就是:
---------------------------------------------------------------------------------------------------------------------------------
呼~ 终于得到了一个像样的函数了!诶?我们要求的是什么来着?
----是系数w和b啊
那怎么办?P函数里根本没有这两个值啊?
相信细心的小伙伴已经发现了,我们的里不久含有w和b吗!
= |
- y | 而
= wx+b
好了,现在我们的函数P就完全是一个除了w和b以外都是已知数的函数了,这里再强调一下我们要做的事情:
P函数代表着所有这些误差点发生的总概率,而事实就是这些误差点已经发生了,正如前面讲到的最大似然一样,我们要找出相应的w和b使这个概率P达到最大值,也就是找到最适合的w和b使得误差点的分布最有可能是真实值的分布(因为此时的w和b刚好能使该事件发生的概率P最大,所以说是最有可能,就像摸球案例中的黑球最有可能的占比是70%)
---------------------------------------------------------------------------------------------------------------------------------
综上所述,现在这个问题就完全变成了函数求最大值的数学问题:我们要找到最合适的w和b,使得我们的总概率P的函数值最大!
这里我们再做一下数据上的扩展,方便各位小伙伴们后续跟着驼鹿一起推导出更一般的公式:我们假设真实值y不仅只与一个特征x有关,而是与多个特征(x1,x2,x3,...,xn)都有关系,那么自然地,每一个特征x都会对应着一个属于他自己的权重w,即权重分别是(w1,w2,w3,......,wn),那么我们的预测值就可以写成 =w1*x1+w2*x2+......+wn*xn+b ,把(x1,x2,x3,...,xn)和(w1,w2,w3,......,wn)看成是行向量(矩阵),就可以写出预测值的矩阵形式的公式 :
![]() (其中b看成w0即可,他与x的0次幂相乘)
(其中b看成w0即可,他与x的0次幂相乘)
那现在我们的P就可以写成:
接下来用数学方法对他求最值:
先两边取对数变连成为连加:

整理一下可得:

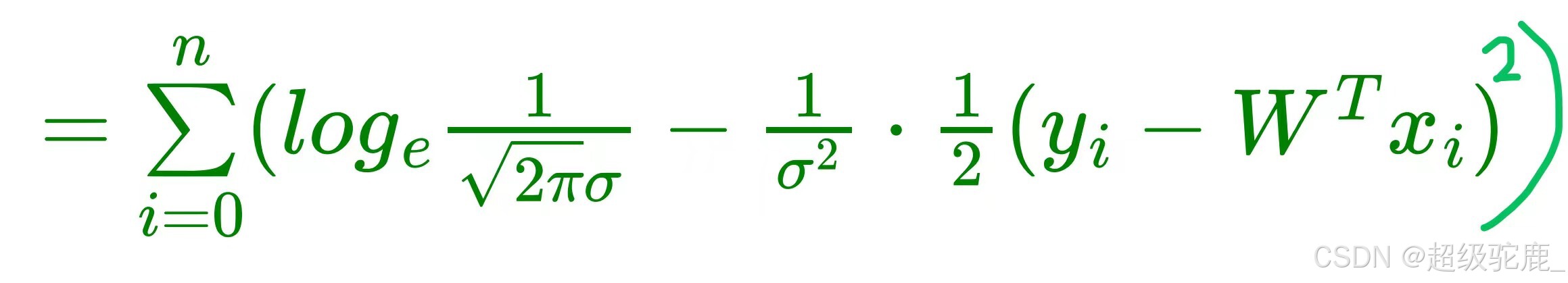
观察一下上式可以发现 ![]() 完全就是常数,
完全就是常数,![]() 也是个常数,故欲使P函数最大,等
也是个常数,故欲使P函数最大,等
价于使![]() 这一部分最小,我们把它记为L函数,代表Loss,也就是损失函数
这一部分最小,我们把它记为L函数,代表Loss,也就是损失函数

---------------------------------------------------------------------------------------------------------------------------------
哈哈哈这个函数是不是很眼熟?没错,它就是我们的最小二乘法,也就是MSE:mean_square_error 的损失函数!相信许多小伙伴们都能背出来它的解!我们现在再来推导一遍:
注意到要累加x,所以我们想的是将x(i)的累加和变成矩阵形式的X,相应地,W也等价的换成符号,那么现在我们就可以扔掉外面的累加号(利用矩阵乘法的特性),把它变成简洁的矩阵形式:

(注意函数名的变化仅仅是因为自变量改变了所以重新起了个名字)
根据矩阵运算法则将其展开:

求导:

令导数等于零有:

注意!!矩阵没有除法哦,不能直接相消!利用逆矩阵:

这样,我们就求出来了 也就是权重w的解!!
---------------------------------------------------------------------------------------------------------------------------------
把它应用到我们的损失函数L上:就求得了w和b的值(也就是W矩阵)!!!
至此,我们的线性回归推导就完美实现了!!!!!!
---------------------------------------------------------------------------------------------------------------------------------
呼~,看到这里,相信各位小伙伴已经很清楚AI机器学习中最基本的线性回归算法是如何来的了,但驼鹿还有一些想补充的:这种估计方法,我们假设了误差的出现是随机且独立的,如果误差不是那么这个模型肯定就会有失偏颇,可能我们需要用泊松分布、均匀分布,那我们就需要重新推导一下。
---------------------------------------------------------------------------------------------------------------------------------
最后的最后,欢迎大家在讨论区提出疑问或者指正驼鹿的小文章,如果你还想继续了解有关AI算法的最底层原理和推导,或是其他和AI相关的技术,请关注超级驼鹿的账号,我会持续更新!
---------------------------------------------------------------------------------------------------------------------------------























 1549
1549

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








