线性回归原理推导

XY_souga

已于 2022-12-01 19:02:57 修改

阅读量1.4k

点赞数 2

文章标签：线性回归算法

于 2022-09-12 22:22:25 首次发布

本文链接：https://blog.csdn.net/dd_souga/article/details/126813861

版权

一、参数公式推导

1、线性回归方程
在三维空间中，决策面/预测函数可表示为：
$h_θ(x)=θ_0+θ_1x_1+θ_2x_2$ ，其中 $θ_0$ 是截距，又称偏置项。

我们添加一个 $x_0$ ，并将其值设置为1，则上式在多维空间中可表示为矩阵形式：
$h_θ(x)=\displaystyle\sum_{i=0}^nθ_ix_i=θ^Tx$ ，转换为矩阵形式可方便计算。
2、确定求参方程
设真实值与预测值之间的误差为 $ε^{(i)}$ ，回归方程要求：
误差 $ε^{(i)}$ 独立、具有相同分布，且服从均值为0方差为 $θ^2$ 的高斯分布(或正态分布)。
为什么做这样的假设：
用数学理论解释： 正态分布和同方差假设是为了保证回归在小样本下能够顺利进行假设检验，同时同方差则保证经典的最小二乘法估计出来的统计量具备最小方差(即保证有效性)。正态分布假设仅在小样本下是需要的，大样本下则不需要，因为大样本有大数定理和中心极限定理作支撑，后者可以保证正态性。同方差、正态性是一个标准模型，其它更复杂的模型都是放松一些假定后得到的。
用业务思维解释： 作这样的假设是为了说明，离散的数据点是沿着拟合直线的两侧均匀分布的，即我们的拟合直线是“靠谱”的。

预测值与误差： $y^{(i)}=θ^Tx^{(i)}+ε^{(i)}$ ①
由于误差服从高斯分布，且均值为0，故误差函数为： $p(ε^{(i)})=\frac{1}{ \sqrt{2π}σ}exp(-\frac{(ε^{(i)})^2}{2σ^2})$ ②

利用误差的高斯分布求 $θ$ ，将①式代入②式得：
$p(y^{(i)}|x^{(i)};θ)=\frac{1}{ \sqrt{2π}σ}exp(-\frac{(y^{(i)}-θ^Tx^{(i)})^2}{2σ^2})$ ，如此消去ε得到关于θ的公式。

似然函数是用来求可能性的，至于y与误差分布与似然函数之间的关系，待补充。转化为似然函数，得：
$L(θ)=\displaystyle\prod_{i=1}^mp(y^{(i)}|x^{(i)};θ)=\displaystyle\prod_{i=1}^m\frac{1}{ \sqrt{2π}σ}exp(-\frac{(y^{(i)}-θ^Tx^{(i)})^2}{2σ^2})$

上式涉及到乘法，不好计算，利用对数将乘法转化为加法，由于我们求的是关于 $θ$ 的极值点的位置，这个转换虽会影响极值的大小，但不影响极值点的位置，故转换是合理的，转换后得对数似然：
$\log L(θ)=\log\displaystyle\prod_{i=1}^m\frac{1}{ \sqrt{2π}σ}exp(-\frac{(y^{(i)}-θ^Tx^{(i)})^2}{2σ^2})$

展开化简得： $\displaystyle\sum_{i=1}^m\log\frac{1}{ \sqrt{2π}σ}exp(-\frac{(y^{(i)}-θ^Tx^{(i)})^2}{2σ^2})$

= $m\log\frac{1}{ \sqrt{2π}σ}-\frac{1}{σ^2}.\frac{1}{2}\displaystyle\sum_{i=1}^m(y^{(i)}-θ^Tx^{(i)})^2$

因为，似然函数（对数变换后也一样）越大越好，故让目标函数：
$J(θ)=\frac{1}{2}\displaystyle\sum_{i=1}^m(y^{(i)}-θ^Tx^{(i)})^2$ ，越小越好（最小二乘法）
对目标函数 $J(θ)=\frac{1}{2}\displaystyle\sum_{i=1}^m\left(h_θ(x^{(i)})-y^{(i)}\right)^2=\frac{1}{2}(Xθ-y)^T(Xθ-y)$ ，求偏导(矩阵的平方=矩阵的转置它自身)：
$\nabla_θJ(θ)=\nabla_θ\left(\frac{1}{2}(Xθ-y)^T(Xθ-y)\right)=\nabla_θ\left(\frac{1}{2}(θ^TX^T-y^T)(Xθ-y)\right)$
= $\nabla_θ\left(\frac{1}{2}(θ^TX^TXθ-θ^TX^Ty-y^TXθ+y^Ty)\right)$
= $\frac{1}{2}\left(2X^TXθ-X^Ty-(y^TX)^T\right)=X^TXθ-X^Ty$
令偏导等于0且等式两边同时乘以逆矩阵(矩阵逆矩阵=单位矩阵，单位矩阵都是1，可消)：
$θ=(X^TX)^{-1}X^Ty$ ，当 $X^TX)^{-1}$ 存在时成立。
至此，我们得到了求参数θ的方程，此方程需满足两个条件：
①误差 $ε^{(i)}$ 独立、具有相同分布，且服从均值为0方差为 $θ^2$ 的高斯分布(或正态分布)；
② $X^TX)^{-1}$ 存在。

二、机器学习求解参数

我们通过上节得到的参数公式，直接代入样本数值求解参数，显然无法得知该参数是否是最优解解；甚至有的参数公式无法直接求解(线性回归是一个特列)，而机器学习则可以解决这个问题。机器学习的常规套路是给它一个样本，然后告诉它按着某个正确的思路去做，结果就是我们要找的；这个过程就是机器学习的功能，也是它智能化的体现。

1、梯度下降算法。
对于线性回归来说，这个思路就是梯度下降算法；其它，所有求解最小值的方法都可以用梯度下降。梯度下降算法每次只求解一个参数，因为特征量是相互独立的，所以参数也是相互独立的，故这个思路是合理的。

目标函数： $J(θ_0,θ_1)=\frac{1}{2m}\displaystyle\sum_{i=1}^m\left(h_θ(x^{(i)})-y^{(i)}\right)^2$ ，其中m指取平均。
求解第j个参数，则要对 $θ_j$ 求偏导：
$\frac{\partial J(θ)}{\partial θ_j}=-\frac{1}{m}\displaystyle\sum_{i=i}^m\left(y^i-h_θ(x^i)\right)x_j^i$ ，其中i表示第i个样本。

批量梯度下降： $θ_j=θ_j+\frac{1}{m}\displaystyle\sum_{i=1}^m\left(y^i-h_θ(x^i)\right)x_j^i$ 。 $θ_j$ 每次移动都使用全部的样本量，循环迭代样本，直到 $θ_j$ 达到稳定状态。优点是每次都考虑所有样本，取所有样本结果的均值，容易得到最优解；缺点是计算量大、速度慢（注意m前的正负号变换，偏导本身不表示方向，仅表示最小位移量，我们在 $θ_j$ 的基础上减去这个“最小位移量”才是指明了移动方向，因此 $θ_j$ 要沿着我们指明的这个方向走）。

单样本随机梯度下降： $θ_j=θ_j+\left(y^i-h_θ(x^i)\right)x_j^i$ 。每次只用一个样本；优点是迭代速度快、计算量小；缺点是不一定每次都朝着收敛的方向移动，尤其当样本中含有异常点时，会导致 $θ_j$ 波动幅度大。

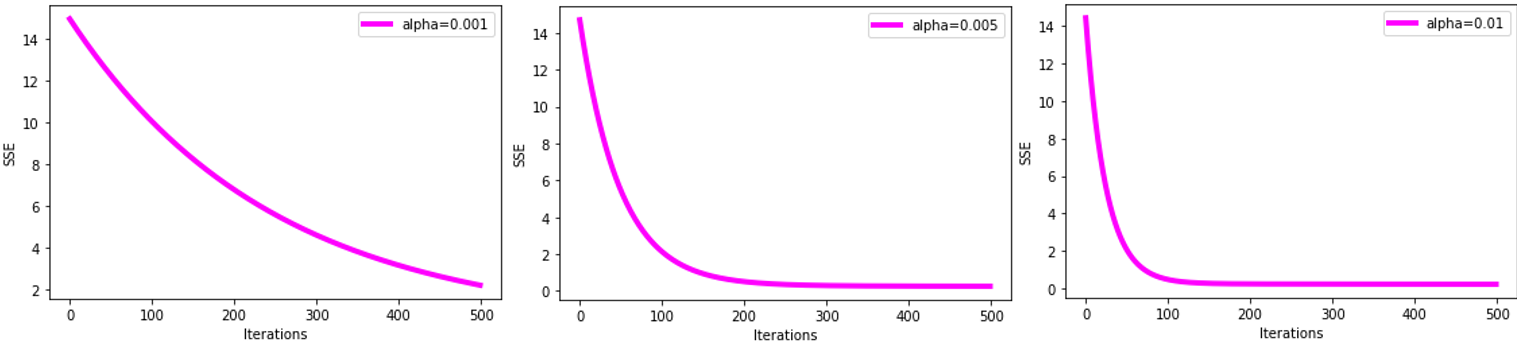
小批量随机梯度下降： $θ_j=θ_j-α\frac{1}{10}\displaystyle\sum_{k=i}^{i+9}\left(h_θ(x^{(k)})-y^{(k)}\right)x_j^{(k)}$ ，每次选取样本中的一部分样本进行迭代；这里的 $\frac{1}{10}$ 指10个样本的均值，样本容量k按照个人经验给出，一般根据项目紧急程度、电脑性能来确定，越大越精确，实际经验是最低64个；α为移动步长，根据经验选择0.005、0.01等很小的值（实际上，当α=0.001时，迭代500次仍不能收敛；而α=0.005时，迭代200次可收敛；当α=0.01时，收敛速度更快，100次即可收敛）。此法综合了批量梯度、单样本随机梯度的优缺点，是最常用的方法。

2、实验效果
不同步长，误差平方和的收敛速度：
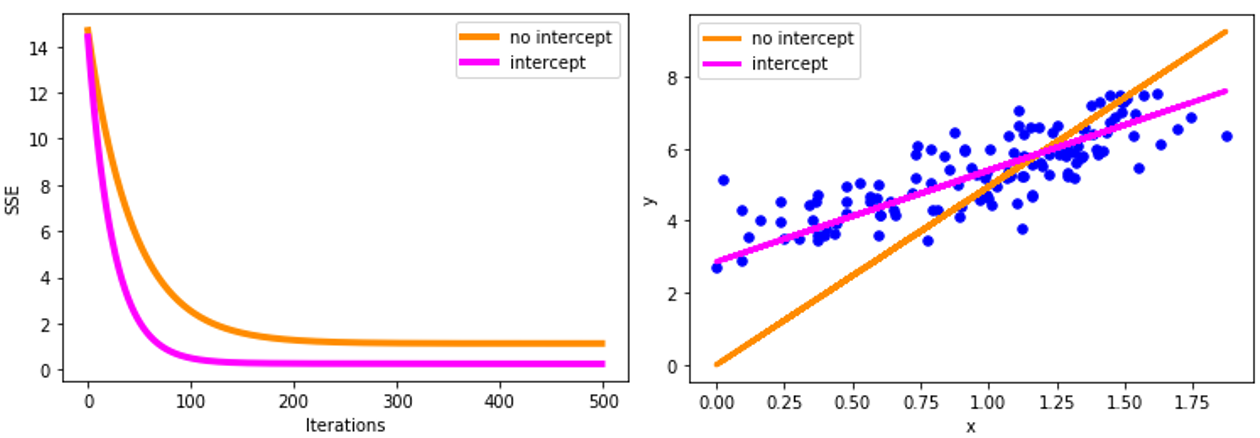
在这里插入图片描述
保留截距与不保留截距的效果：

三、局部加权线性回归

1、作用
（1）预测问题：有周期性、波动性的数据，简单的线性拟合效果不好，误差较大；局部加权线性回归可提高拟合精度；
（2）平滑问题：局部加权回归（lowess）也能较好的解决平滑问题。在做数据平滑的时候，会有遇到有趋势或者季节性的数据，对于这样的数据，我们不能使用简单的均值正负3倍标准差以外做异常值剔除，需要考虑到趋势性等条件。使用局部加权回归，可以拟合一条趋势线，将该线作为基线，偏离基线距离较远的则是真正的异常值点。
实际上，局部加权回归（Lowess）主要还是处理平滑问题的多，因为预测问题，可以有更多模型做的更精确。但就平滑来说，Lowess很直观而且很有说服力。
2、原理： 赋予待测点附件每个点不同的权重，在待测点附近这个子集上基于最小均方差进行回归；即算法更重视那些距离待测点 $x$ 近的点，使距离待测点 $x$ 近的样本点的损失小，如此达到准确预测的目标。
为避免混淆，用W矩阵表示权重，用θ矩阵表示参数。
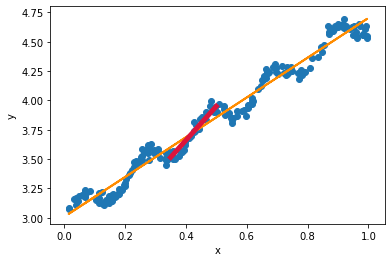
在这里插入图片描述
如图所示，黄线为普通线性拟合，区间[0.35,0.5]是待测点x=0.425附件的一个范围；若在x∈[0.35,0.5]区间上用红线拟合，那么就能提高拟合精度。即，在区间[0.35,0.5]上设置样本点的权重为1，在区间[0.35,0.5]以外，设置样本点的权重为0，那么就能精确的拟合出[0.35,0.5]上的直线。如此，对于每个 $x_i$ ，都能精确的拟合出基于 $x_i$ 为中心点的区间上的一段小直线；假设区间[0.35,0.5]范围越来越小，甚至逼近于0，那么连接每个 $x_i$ 区间上的直线，就会形成一条平滑的曲线。

用数学语言表达：前面知道，线性回归的目标函数/损失函数为
$J(θ)=\frac{1}{2}\displaystyle\sum_{i=1}^m(y^{(i)}-θ^Tx^{(i)})^2$
加上权重 $W^{(i)}$ ，使得损失函数变为 $J(θ)=\frac{1}{2}\displaystyle\sum_{i=1}^mW^{(i)}(y^{(i)}-θ^Tx^{(i)})^2$ ，权重 $W^{(i)}$ 被称为核函数，最常用的核函数为高斯核函数，及
$W^{(i)}=е^{-\frac{(x^{i}-x)^2}{2σ^2}}$ ，高斯核函数的取值范围是(0,1]， $x^{i}$ 是所有样本点， $x$ 是待测样本点；当 $x^{i}$ 靠近待测样本点时，核函数的值越接近于1；当 $x^{i}$ 远离待测样本点时，核函数的值越接近于0。最小化这个损失函数时，算法就能寻找到使得距离 $x$ 越近的样本点的损失较小的 $θ$ 。