CS231n课程作业(一) Two-layer Neural Network

最新推荐文章于 2023-05-29 11:21:45 发布

coder_mckee

最新推荐文章于 2023-05-29 11:21:45 发布

阅读量3.2k

点赞数 6

分类专栏：深度学习文章标签：深度学习

本文链接：https://blog.csdn.net/LeeWanzhi/article/details/79120025

版权

神经网络的过程主要就是forward propagation和backward propagation。
forward propagation to evaluate score function & loss function, then back propagation 对每一层计算loss对W和b的梯度，利用梯度完成W和b的更新。
总体过程可以理解为：forward–>backward–>update–>forward–>backward–>update……

一、理论知识

1. 直观理解

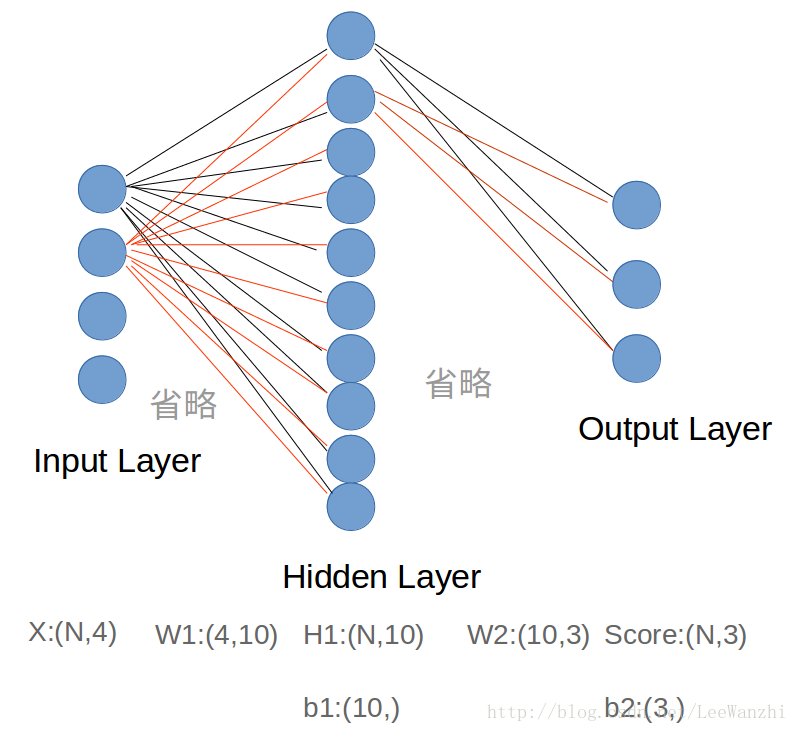
这里写图片描述
这是一个两层的full-connected神经网络，分别是输入层、隐藏层和输出层(输入层不算一层)。输入层4个节点表示样本是4维的，输出层3个节点表示有3类，输出的结果是每个类的score。

FC层(全连接层)：每个神经元都连接上一层的所有神经元的layer。

在神经网络中，bigger = better，即网络模型越大越好。more neurons = more capacity，因为机器学习中经常出现模型表达能力不足的情况。

对于神经网络的更形象理解：
这里写图片描述

2. score function

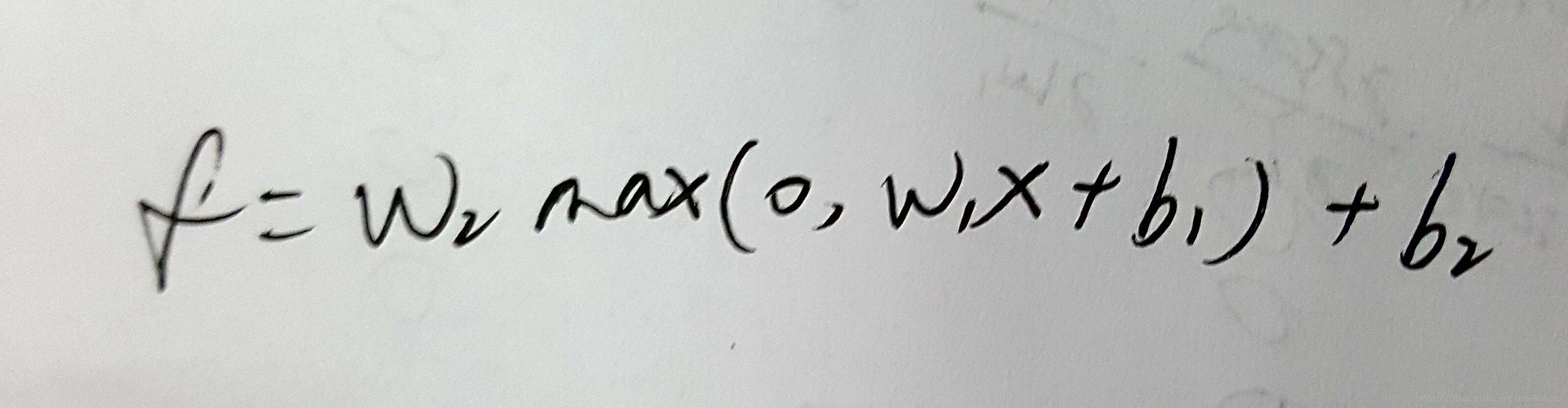
这里写图片描述
这里activation function采用的是ReLU函数。
Why we set activation function？
answer：如果不设置activation function，则每层的output都是input的线性函数，则无论隐藏层有多少层，都与没有隐藏层效果一样。因此，设置activation function，目的是为了对input进行非线性转化，然后output，使神经网络更有意义。

3. loss function及求梯度

本次作业中使用的是softmax loss function。可参考softmax classifier。
完成作业的关键仍是loss function对W求梯度。下面求gradient(注意：我在角标表示上有错误，但不影响理解和代码化)：
这里写图片描述
这样，score、loss和gradient都表达出来了，2层神经网络也就可以完成了。

二、Two-layer Neural Network

1. Forward Propagation & Backward Propagation

Forward: 计算score，再根据score计算loss
Backward：分别对W2、b2、W1、b1求梯度

  def loss(self, X, y=None, reg=0.0):
    """
    Compute the loss and gradients for a two layer fully connected neural
    network.

    Inputs:
    - X: Input data of shape (N, D). Each X[i] is a training sample.
    - y: Vector of training labels. y[i] is the label for X[i], and each y[i] is
      an integer in the range 0 <= y[i] < C. This parameter is optional; if it
      is not passed then we only return scores, and if it is passed then we
      instead return the loss and gradients.
    - reg: Regularization strength.

    Returns:
    If y is None, return a matrix scores of shape (N, C) where scores[i, c] is
    the score for class c on input X[i].

    If y is not None, instead return a tuple of:
    - loss: Loss (data loss and regularization loss) for this batch of training
      samples.
    - grads: Dictionary mapping parameter names to gradients of those parameters
      with respect to the loss function; has the same keys as self.params.
    """
    # Unpack variables from the params dictionary
    W1, b1 = self.params['W1'], self.params['b1']
    W2, b2 = self.params['W2'], self.params['b2']
    N, D = X.shape

    # Compute the forward pass
    scores = None
    #############################################################################
    # TODO: Perform the forward pass, computing the class scores for the input. #
    # Store the result in the scores variable, which should be an array of      #
    # shape (N, C).                                                             #
    #############################################################################
    h1 = np.maximum(0, np.dot(X,W1) + b1) #(5,10)
    #print (h1.shape)
    scores = np.dot(h1,W2) + b2 # (5,3)

最低0.47元/天解锁文章